Question and Answers Forum
Question Number 69681 by ajfour last updated on 26/Sep/19
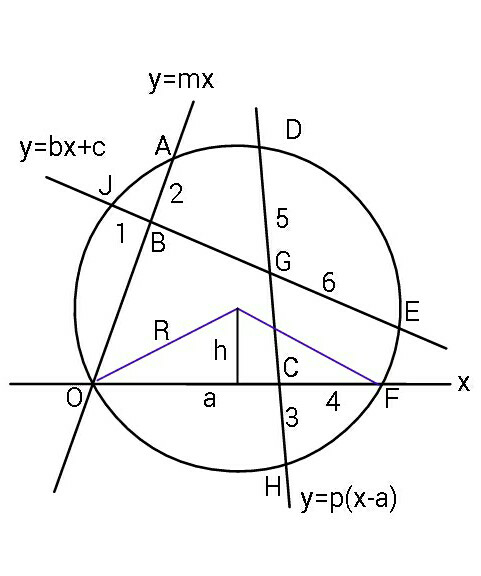
Commented by ajfour last updated on 26/Sep/19
Commented by ajfour last updated on 26/Sep/19

Answered by ajfour last updated on 30/Sep/19
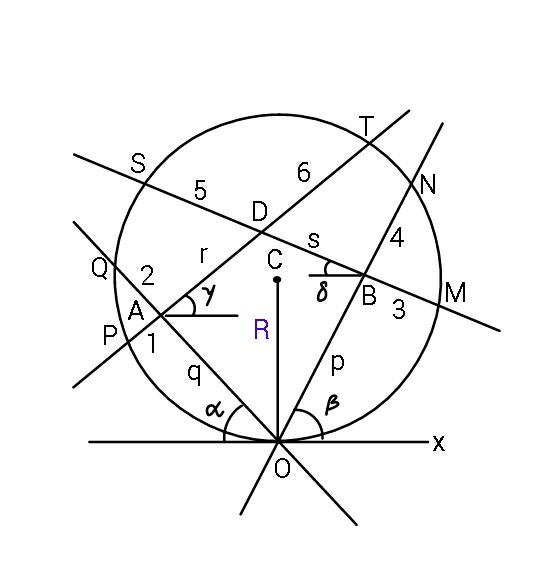
Commented by ajfour last updated on 30/Sep/19
![let cos α=a, cos β=h, cos γ=m, cos δ=u & sin α=b, sin β=k, sin γ=n, sin δ=v x_D =−qa+rm=ph−su ⇒ su+rm = qa+ph ...(i) y_D =qb+rn=pk+sv ⇒ sv−rn = qb−pk ...(ii) ∣CP ∣=R =∣CT∣ ⇒ _________________________ (−qa−m)^2 +(qb−n−R)^2 =R^2 [−qa+(r+6)m]^2 +(qb+(r+6)n−R]^2 =R^2 ⇒ r+6 and −1 are roots of eq. (−qa+mx)^2 +(qb+nx−R)^2 =R^2 (m^2 +n^2 )x^2 +2x[−qam+n(qb−R)] +q^2 a^2 +q^2 b^2 +R^2 −2qbR−R^2 =0 ⇒ x^2 +2x[−qam+n(qb−R)] +q^2 −2qbR=0 _________________________ ⇒ r+5=qam−n(qb−R) & m^2 +n^2 =1 .....(iii),(iv) [r+5+n(qb−R)]^2 =q^2 a^2 (1−n^2 ) ⇒ n^2 {(qb−R)^2 +q^2 a^2 }+ +2(r+5)(qb−R)n+(r+5)^2 −q^2 a^2 =0 _________________________ ∣CM∣=R =∣CS∣ ⇒ (ph+3u)^2 +(pk−3v−R)^2 =R^2 [ph−(s+5)u]^2 +[pk+(s+5)v−R]^2 =R^2 ⇒ s+5 and −3 are roots of eq. (ph−ux)^2 +(pk+vx−R)^2 =R^2 _________________________ ⇒ sum of roots (s+5)+(−3)= s+2=phu−v(pk−R) (as h^2 +k^2 =1) & u^2 +v^2 =1 ......(v),(vi) _________________________ plus _________________________ a^2 +b^2 =1 , h^2 +k^2 =1 ..(vii)&(viii) 2q=r+6 ....(ix) 4p=3(s+5) ....(x) 5(s+3)=6(r+1) ....(xi) further 2bR=q+2 & ..(xii) 2kR=p+4 ....(xiii) Thirteen eqs. in thirteen unknowns a,b,h,k,m,n,u,v,p,q,r,s,&R.](Q70067.png)
Answered by mr W last updated on 30/Sep/19
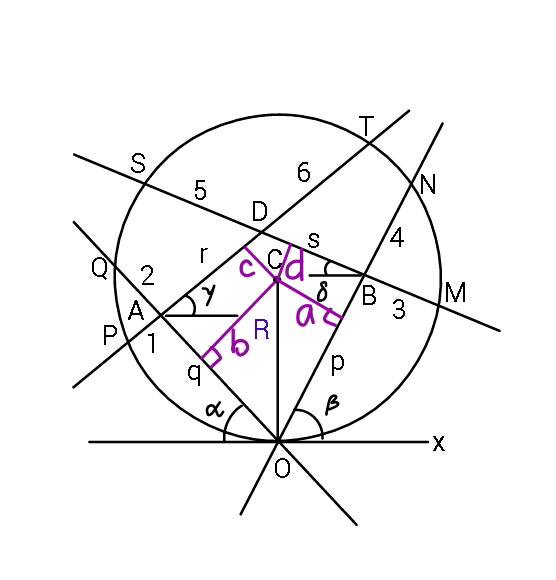
Commented by mr W last updated on 30/Sep/19
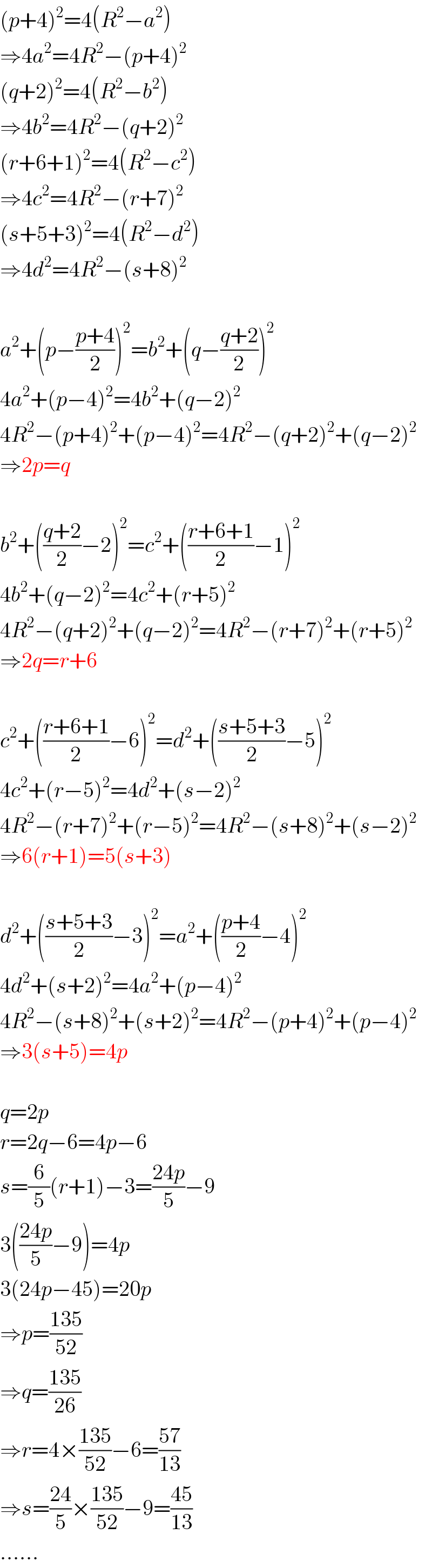
Commented by mr W last updated on 30/Sep/19
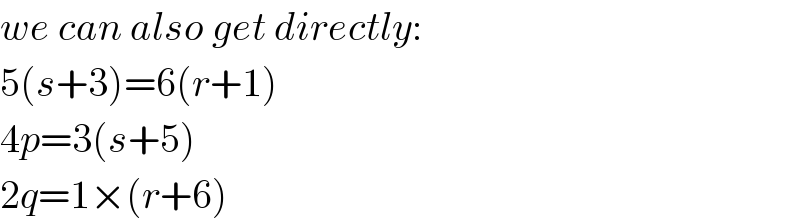
Commented by ajfour last updated on 01/Oct/19
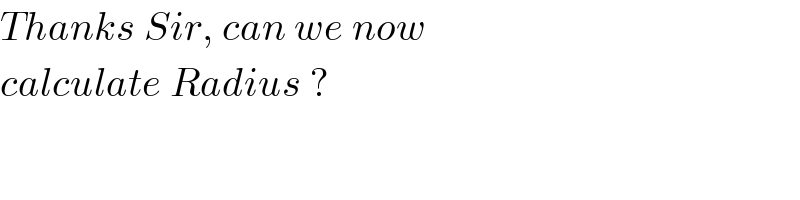
Commented by mr W last updated on 02/Oct/19