Question Number 69766 by Rio Michael last updated on 27/Sep/19
$${find}\:\:\frac{{dy}}{{dx}}\:\:{at}\:{the}\:{point}\:\:\left(\mathrm{0},\mathrm{3}\right)\:\:{when}\:\:\mathrm{2}{x}^{\mathrm{2}} {y}\:+\:{y}\:+\:\mathrm{4}{xy}^{\mathrm{2}} \:=\:\mathrm{2}{x}\:+\:\mathrm{3}\: \\ $$
Commented by kaivan.ahmadi last updated on 27/Sep/19
$${f}\left({x},{y}\right)=\mathrm{2}{x}^{\mathrm{2}} {y}+{y}+\mathrm{4}{xy}^{\mathrm{2}} −\mathrm{2}{x}−\mathrm{3}=\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}=−\frac{{f}_{{x}} '}{{f}_{{y}} '}=−\frac{\mathrm{4}{xy}+\mathrm{4}{y}^{\mathrm{2}} −\mathrm{2}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}+\mathrm{4}{x}}\mid_{\left(\mathrm{0},\mathrm{3}\right)} =−\frac{\mathrm{4}\left(\mathrm{3}\right)^{\mathrm{2}} −\mathrm{2}}{\mathrm{1}}=−\mathrm{34} \\ $$
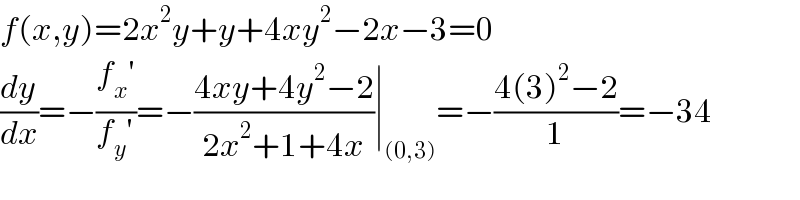
Commented by MJS last updated on 27/Sep/19
![implicit differentiation ((d/dx)[f(x, y)])dx=−((d/dy)[f(x, y)])dy on the l.h.s treat y as a constant on the r.h.s treat x as a constant ⇒ it′s easy to calculate (dx/dy) and (dy/dx) at the end put x=0, y=3 in this case f(x, y)=2x^2 y+4xy^2 +y−2x−3 I think now you can do it](Q69776.png)
$$\mathrm{implicit}\:\mathrm{differentiation} \\ $$$$\left(\frac{{d}}{{dx}}\left[{f}\left({x},\:{y}\right)\right]\right){dx}=−\left(\frac{{d}}{{dy}}\left[{f}\left({x},\:{y}\right)\right]\right){dy} \\ $$$$\mathrm{on}\:\mathrm{the}\:\mathrm{l}.\mathrm{h}.\mathrm{s}\:\mathrm{treat}\:{y}\:\mathrm{as}\:\mathrm{a}\:\mathrm{constant} \\ $$$$\mathrm{on}\:\mathrm{the}\:\mathrm{r}.\mathrm{h}.\mathrm{s}\:\mathrm{treat}\:{x}\:\mathrm{as}\:\mathrm{a}\:\mathrm{constant} \\ $$$$\Rightarrow\:\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{calculate}\:\frac{{dx}}{{dy}}\:\mathrm{and}\:\frac{{dy}}{{dx}} \\ $$$$\mathrm{at}\:\mathrm{the}\:\mathrm{end}\:\mathrm{put}\:{x}=\mathrm{0},\:{y}=\mathrm{3} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case} \\ $$$${f}\left({x},\:{y}\right)=\mathrm{2}{x}^{\mathrm{2}} {y}+\mathrm{4}{xy}^{\mathrm{2}} +{y}−\mathrm{2}{x}−\mathrm{3} \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{now}\:\mathrm{you}\:\mathrm{can}\:\mathrm{do}\:\mathrm{it} \\ $$
Commented by Rio Michael last updated on 27/Sep/19
$${sure}\:{sir}\: \\ $$$$\:\mathrm{4}{xy}\:+\:\mathrm{2}{x}^{\mathrm{2}} \frac{{dy}}{{dx}}\:+\:\mathrm{4}{y}^{\mathrm{2}} \:+\:\mathrm{8}{xy}\frac{{dy}}{{dx}}\:+\:\frac{{dy}}{{dx}}\:=\:\mathrm{2}\: \\ $$$$\mathrm{2}{x}^{\mathrm{2}} \frac{{dy}}{{dx}}\:+\:\mathrm{8}{xy}\frac{{dy}}{{dx}}\:+\:\frac{{dy}}{{dx}}\:=\:\mathrm{2}\:−\mathrm{4}{xy}\:−\:\mathrm{4}{y}^{\mathrm{2}} \\ $$$$\frac{{dy}}{{dx}}\left(\mathrm{2}{x}^{\mathrm{2}} \:+\:\mathrm{8}{xy}\:+\:\mathrm{1}\right)\:=\:\mathrm{2}\left(\mathrm{1}\:−\:\mathrm{2}{xy}\:−\mathrm{2}\right) \\ $$$$\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{2}\left(\mathrm{1}\:−\mathrm{2}{xy}−\mathrm{2}\right)}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{8}{xy}\:+\:\mathrm{1}} \\ $$$${x}\:=\mathrm{0}\:{and}\:{y}\:=\:\mathrm{3} \\ $$$$\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{2}\right)}{\mathrm{1}}\:=\:−\mathrm{2}\:\:{is}\:{that}\:{correct}? \\ $$
Commented by MJS last updated on 27/Sep/19
![(d/dx)[2x^2 y+4xy^2 +y−2x−3]=4xy+4y^2 −2 (d/dy)[2x^2 y+4xy^2 +y−2x−3]=2x^2 +8xy+1 (4xy+4y^2 −2)dx=−(2x^2 +8xy+1)dy (dy/dx)=−((4xy+4y^2 −2)/(2x^2 +8xy+1)) x=0∧y=3 ⇒ (dy/dx)=−((34)/1)=−34](Q69796.png)
$$\frac{{d}}{{dx}}\left[\mathrm{2}{x}^{\mathrm{2}} {y}+\mathrm{4}{xy}^{\mathrm{2}} +{y}−\mathrm{2}{x}−\mathrm{3}\right]=\mathrm{4}{xy}+\mathrm{4}{y}^{\mathrm{2}} −\mathrm{2} \\ $$$$\frac{{d}}{{dy}}\left[\mathrm{2}{x}^{\mathrm{2}} {y}+\mathrm{4}{xy}^{\mathrm{2}} +{y}−\mathrm{2}{x}−\mathrm{3}\right]=\mathrm{2}{x}^{\mathrm{2}} +\mathrm{8}{xy}+\mathrm{1} \\ $$$$\left(\mathrm{4}{xy}+\mathrm{4}{y}^{\mathrm{2}} −\mathrm{2}\right){dx}=−\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{8}{xy}+\mathrm{1}\right){dy} \\ $$$$\frac{{dy}}{{dx}}=−\frac{\mathrm{4}{xy}+\mathrm{4}{y}^{\mathrm{2}} −\mathrm{2}}{\mathrm{2}{x}^{\mathrm{2}} +\mathrm{8}{xy}+\mathrm{1}} \\ $$$${x}=\mathrm{0}\wedge{y}=\mathrm{3}\:\Rightarrow\:\frac{{dy}}{{dx}}=−\frac{\mathrm{34}}{\mathrm{1}}=−\mathrm{34} \\ $$