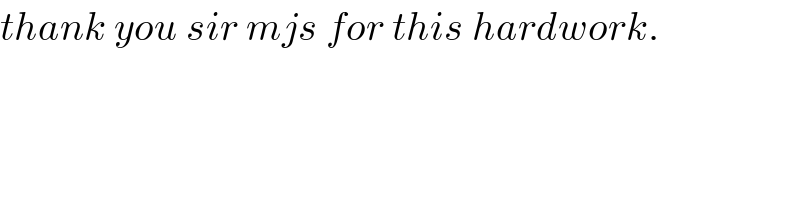Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 69792 by mathmax by abdo last updated on 27/Sep/19

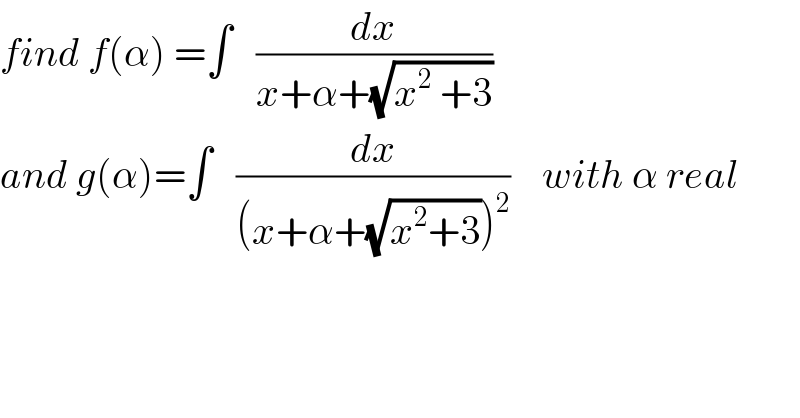
find f(α) =∫ (dx/(x+α+(√(x^2 +3)))) and g(α)=∫ (dx/((x+α+(√(x^2 +3)))^2 )) with α real

$${find}\:{f}\left(\alpha\right)\:=\int\:\:\:\frac{{dx}}{{x}+\alpha+\sqrt{{x}^{\mathrm{2}} \:+\mathrm{3}}} \\ $$$${and}\:{g}\left(\alpha\right)=\int\:\:\:\frac{{dx}}{\left({x}+\alpha+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right)^{\mathrm{2}} }\:\:\:\:{with}\:\alpha\:{real} \\ $$

Commented by mathmax by abdo last updated on 10/Oct/19

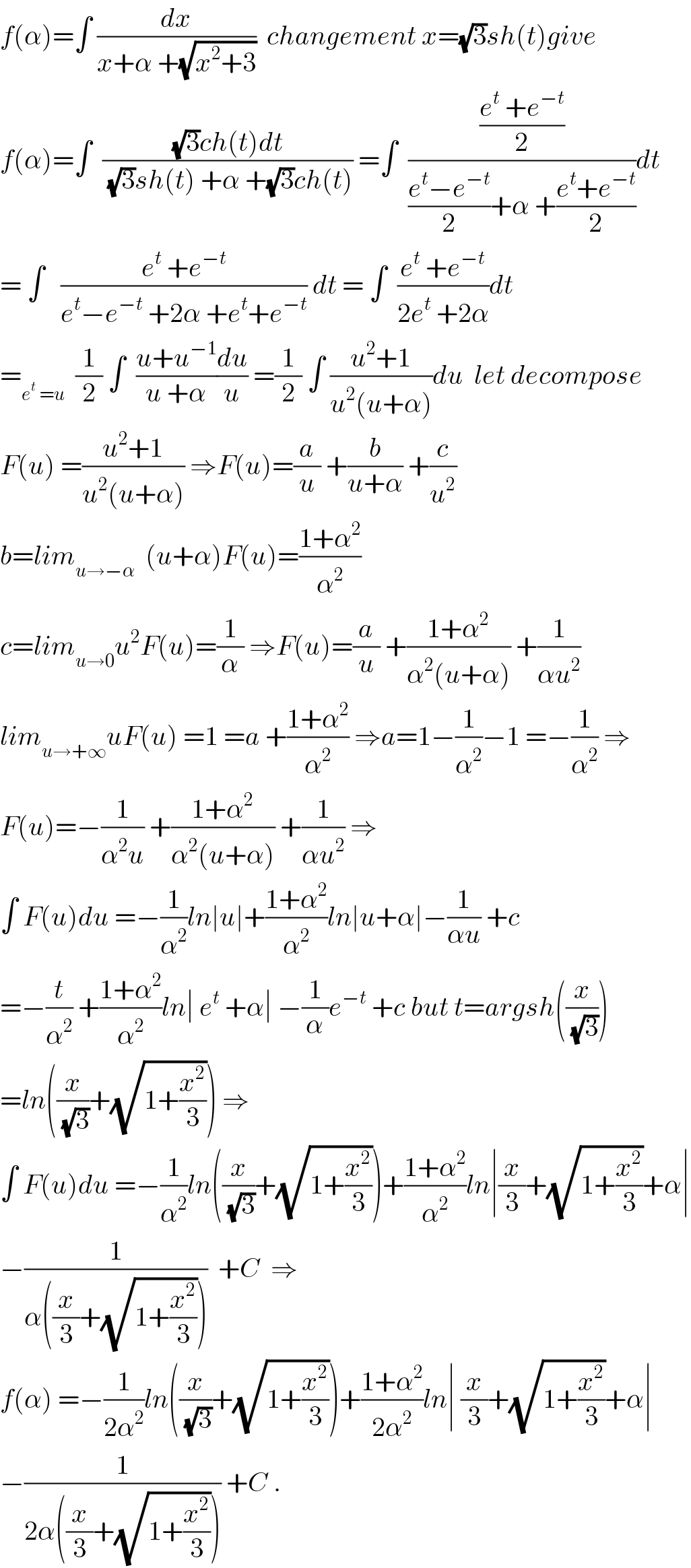
f(α)=∫ (dx/(x+α +(√(x^2 +3)))) changement x=(√3)sh(t)give f(α)=∫ (((√3)ch(t)dt)/((√3)sh(t) +α +(√3)ch(t))) =∫ (((e^t +e^(−t) )/2)/(((e^t −e^(−t) )/2)+α +((e^t +e^(−t) )/2)))dt = ∫ ((e^t +e^(−t) )/(e^t −e^(−t) +2α +e^t +e^(−t) )) dt = ∫ ((e^t +e^(−t) )/(2e^t +2α))dt =_(e^t =u) (1/2) ∫ ((u+u^(−1) )/(u +α))(du/u) =(1/2) ∫ ((u^2 +1)/(u^2 (u+α)))du let decompose F(u) =((u^2 +1)/(u^2 (u+α))) ⇒F(u)=(a/u) +(b/(u+α)) +(c/u^2 ) b=lim_(u→−α) (u+α)F(u)=((1+α^2 )/α^2 ) c=lim_(u→0) u^2 F(u)=(1/α) ⇒F(u)=(a/u) +((1+α^2 )/(α^2 (u+α))) +(1/(αu^2 )) lim_(u→+∞) uF(u) =1 =a +((1+α^2 )/α^2 ) ⇒a=1−(1/α^2 )−1 =−(1/α^2 ) ⇒ F(u)=−(1/(α^2 u)) +((1+α^2 )/(α^2 (u+α))) +(1/(αu^2 )) ⇒ ∫ F(u)du =−(1/α^2 )ln∣u∣+((1+α^2 )/α^2 )ln∣u+α∣−(1/(αu)) +c =−(t/α^2 ) +((1+α^2 )/α^2 )ln∣ e^t +α∣ −(1/α)e^(−t) +c but t=argsh((x/(√3))) =ln((x/(√3))+(√(1+(x^2 /3)))) ⇒ ∫ F(u)du =−(1/α^2 )ln((x/(√3))+(√(1+(x^2 /3))))+((1+α^2 )/α^2 )ln∣(x/3)+(√(1+(x^2 /3)))+α∣ −(1/(α((x/3)+(√(1+(x^2 /3)))))) +C ⇒ f(α) =−(1/(2α^2 ))ln((x/(√3))+(√(1+(x^2 /3))))+((1+α^2 )/(2α^2 ))ln∣ (x/3)+(√(1+(x^2 /3)))+α∣ −(1/(2α((x/3)+(√(1+(x^2 /3)))))) +C .

$${f}\left(\alpha\right)=\int\:\frac{{dx}}{{x}+\alpha\:+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}\:\:{changement}\:{x}=\sqrt{\mathrm{3}}{sh}\left({t}\right){give} \\ $$$${f}\left(\alpha\right)=\int\:\:\frac{\sqrt{\mathrm{3}}{ch}\left({t}\right){dt}}{\sqrt{\mathrm{3}}{sh}\left({t}\right)\:+\alpha\:+\sqrt{\mathrm{3}}{ch}\left({t}\right)}\:=\int\:\:\frac{\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}}}{\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}+\alpha\:+\frac{{e}^{{t}} +{e}^{−{t}} }{\mathrm{2}}}{dt} \\ $$$$=\:\int\:\:\:\frac{{e}^{{t}} \:+{e}^{−{t}} }{{e}^{{t}} −{e}^{−{t}} \:+\mathrm{2}\alpha\:+{e}^{{t}} +{e}^{−{t}} }\:{dt}\:=\:\int\:\:\frac{{e}^{{t}} \:+{e}^{−{t}} }{\mathrm{2}{e}^{{t}} \:+\mathrm{2}\alpha}{dt} \\ $$$$=_{{e}^{{t}} \:={u}} \:\:\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\frac{{u}+{u}^{−\mathrm{1}} }{{u}\:+\alpha}\frac{{du}}{{u}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{{u}^{\mathrm{2}} +\mathrm{1}}{{u}^{\mathrm{2}} \left({u}+\alpha\right)}{du}\:\:{let}\:{decompose} \\ $$$${F}\left({u}\right)\:=\frac{{u}^{\mathrm{2}} +\mathrm{1}}{{u}^{\mathrm{2}} \left({u}+\alpha\right)}\:\Rightarrow{F}\left({u}\right)=\frac{{a}}{{u}}\:+\frac{{b}}{{u}+\alpha}\:+\frac{{c}}{{u}^{\mathrm{2}} } \\ $$$${b}={lim}_{{u}\rightarrow−\alpha} \:\:\left({u}+\alpha\right){F}\left({u}\right)=\frac{\mathrm{1}+\alpha^{\mathrm{2}} }{\alpha^{\mathrm{2}} } \\ $$$${c}={lim}_{{u}\rightarrow\mathrm{0}} {u}^{\mathrm{2}} {F}\left({u}\right)=\frac{\mathrm{1}}{\alpha}\:\Rightarrow{F}\left({u}\right)=\frac{{a}}{{u}}\:+\frac{\mathrm{1}+\alpha^{\mathrm{2}} }{\alpha^{\mathrm{2}} \left({u}+\alpha\right)}\:+\frac{\mathrm{1}}{\alpha{u}^{\mathrm{2}} } \\ $$$${lim}_{{u}\rightarrow+\infty} {uF}\left({u}\right)\:=\mathrm{1}\:={a}\:+\frac{\mathrm{1}+\alpha^{\mathrm{2}} }{\alpha^{\mathrm{2}} }\:\Rightarrow{a}=\mathrm{1}−\frac{\mathrm{1}}{\alpha^{\mathrm{2}} }−\mathrm{1}\:=−\frac{\mathrm{1}}{\alpha^{\mathrm{2}} }\:\Rightarrow \\ $$$${F}\left({u}\right)=−\frac{\mathrm{1}}{\alpha^{\mathrm{2}} {u}}\:+\frac{\mathrm{1}+\alpha^{\mathrm{2}} }{\alpha^{\mathrm{2}} \left({u}+\alpha\right)}\:+\frac{\mathrm{1}}{\alpha{u}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\int\:{F}\left({u}\right){du}\:=−\frac{\mathrm{1}}{\alpha^{\mathrm{2}} }{ln}\mid{u}\mid+\frac{\mathrm{1}+\alpha^{\mathrm{2}} }{\alpha^{\mathrm{2}} }{ln}\mid{u}+\alpha\mid−\frac{\mathrm{1}}{\alpha{u}}\:+{c} \\ $$$$=−\frac{{t}}{\alpha^{\mathrm{2}} }\:+\frac{\mathrm{1}+\alpha^{\mathrm{2}} }{\alpha^{\mathrm{2}} }{ln}\mid\:{e}^{{t}} \:+\alpha\mid\:−\frac{\mathrm{1}}{\alpha}{e}^{−{t}} \:+{c}\:{but}\:{t}={argsh}\left(\frac{{x}}{\sqrt{\mathrm{3}}}\right) \\ $$$$={ln}\left(\frac{{x}}{\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}}\right)\:\Rightarrow \\ $$$$\int\:{F}\left({u}\right){du}\:=−\frac{\mathrm{1}}{\alpha^{\mathrm{2}} }{ln}\left(\frac{{x}}{\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}}\right)+\frac{\mathrm{1}+\alpha^{\mathrm{2}} }{\alpha^{\mathrm{2}} }{ln}\mid\frac{{x}}{\mathrm{3}}+\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}}+\alpha\mid \\ $$$$−\frac{\mathrm{1}}{\alpha\left(\frac{{x}}{\mathrm{3}}+\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}}\right)}\:\:+{C}\:\:\Rightarrow \\ $$$${f}\left(\alpha\right)\:=−\frac{\mathrm{1}}{\mathrm{2}\alpha^{\mathrm{2}} }{ln}\left(\frac{{x}}{\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}}\right)+\frac{\mathrm{1}+\alpha^{\mathrm{2}} }{\mathrm{2}\alpha^{\mathrm{2}} }{ln}\mid\:\frac{{x}}{\mathrm{3}}+\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}}+\alpha\mid \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}\alpha\left(\frac{{x}}{\mathrm{3}}+\sqrt{\mathrm{1}+\frac{{x}^{\mathrm{2}} }{\mathrm{3}}}\right)}\:+{C}\:. \\ $$

Answered by MJS last updated on 28/Sep/19

∫(dx/(x+α+(√(x^2 +3))))= [we have to substitute x=(√3)sinh t and then t=ln u ⇒ both in 1 step gives u=((√3)/3)(x+(√(x^2 +3))) → dx=(((√3)(u^2 +1))/(2u^2 ))du x=(((√3)(u^2 −1))/(2u))] =((√3)/2)∫((u^2 +1)/(u^2 ((√3)u+α)))du= =((√3)/(2α))∫(du/u^2 )−(3/(2α^2 ))∫(du/u)+(((√3)(α^2 +3))/(2α^2 ))∫(du/((√3)u+α))= =−((√3)/(2α))u^(−1) −(3/(2α^2 ))ln u +((α^2 +3)/(2α^2 ))ln ((√3)u+α) = =(1/(2α))(x−(√(x^2 +3)))−(3/(2α^2 ))ln (x+(√(x^2 +3))) +((α^2 +3)/(2α^2 ))ln (x+α+(√(x^2 +3))) +C ∫(dx/((x+α+(√(x^2 +3)))^2 ))= [same substitution as above] =((√3)/2)∫((u^2 +1)/(u^2 ((√3)u+α)^2 ))du= =((√3)/(2α^2 ))∫(du/u^2 )−(3/α^3 )∫(du/u)+(((√3)(α^2 +3))/(2α^2 ))∫(du/(((√3)u+α)^2 ))+((3(√3))/α^3 )∫(du/((√3)u+α))= =−((√3)/(2α^2 ))u^(−1) −(3/α^3 )ln u −((α^2 +3)/(2α^2 ((√3)u+α)))+(3/α^3 )ln ((√3)u+α) = =(1/(2α^2 ))(x−(√(x^2 +3)))−(3/α^3 )ln (x+(√(x^2 +3))) −((α^2 +3)/(2α^2 (x+α+(√(x^2 +3)))))+(3/α^3 )ln (x+α+(√(x^2 +3))) +C= =((2αx^2 −6x−α(α^2 +3)−2(αx−3)(√(x^2 +3)))/(2α^2 (2αx+α^2 −3)))+(3/α^3 )ln (−αx+3+α(√(x^2 +3))) +C

$$\int\frac{{dx}}{{x}+\alpha+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}= \\ $$$$\:\:\:\:\:\left[\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{substitute}\:{x}=\sqrt{\mathrm{3}}\mathrm{sinh}\:{t}\:\mathrm{and}\right. \\ $$$$\:\:\:\:\:\:\:\mathrm{then}\:{t}=\mathrm{ln}\:{u} \\ $$$$\:\:\:\:\:\:\:\Rightarrow\:\mathrm{both}\:\mathrm{in}\:\mathrm{1}\:\mathrm{step}\:\mathrm{gives} \\ $$$$\:\:\:\:\:\:\:{u}=\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right)\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{3}}\left({u}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{2}{u}^{\mathrm{2}} }{du} \\ $$$$\left.\:\:\:\:\:\:\:{x}=\frac{\sqrt{\mathrm{3}}\left({u}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{2}{u}}\right] \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\int\frac{{u}^{\mathrm{2}} +\mathrm{1}}{{u}^{\mathrm{2}} \left(\sqrt{\mathrm{3}}{u}+\alpha\right)}{du}= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}\alpha}\int\frac{{du}}{{u}^{\mathrm{2}} }−\frac{\mathrm{3}}{\mathrm{2}\alpha^{\mathrm{2}} }\int\frac{{du}}{{u}}+\frac{\sqrt{\mathrm{3}}\left(\alpha^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{2}\alpha^{\mathrm{2}} }\int\frac{{du}}{\sqrt{\mathrm{3}}{u}+\alpha}= \\ $$$$=−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}\alpha}{u}^{−\mathrm{1}} −\frac{\mathrm{3}}{\mathrm{2}\alpha^{\mathrm{2}} }\mathrm{ln}\:{u}\:+\frac{\alpha^{\mathrm{2}} +\mathrm{3}}{\mathrm{2}\alpha^{\mathrm{2}} }\mathrm{ln}\:\left(\sqrt{\mathrm{3}}{u}+\alpha\right)\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\alpha}\left({x}−\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right)−\frac{\mathrm{3}}{\mathrm{2}\alpha^{\mathrm{2}} }\mathrm{ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right)\:+\frac{\alpha^{\mathrm{2}} +\mathrm{3}}{\mathrm{2}\alpha^{\mathrm{2}} }\mathrm{ln}\:\left({x}+\alpha+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right)\:+{C} \\ $$$$ \\ $$$$\int\frac{{dx}}{\left({x}+\alpha+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right)^{\mathrm{2}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{same}\:\mathrm{substitution}\:\mathrm{as}\:\mathrm{above}\right] \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\int\frac{{u}^{\mathrm{2}} +\mathrm{1}}{{u}^{\mathrm{2}} \left(\sqrt{\mathrm{3}}{u}+\alpha\right)^{\mathrm{2}} }{du}= \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}\alpha^{\mathrm{2}} }\int\frac{{du}}{{u}^{\mathrm{2}} }−\frac{\mathrm{3}}{\alpha^{\mathrm{3}} }\int\frac{{du}}{{u}}+\frac{\sqrt{\mathrm{3}}\left(\alpha^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{2}\alpha^{\mathrm{2}} }\int\frac{{du}}{\left(\sqrt{\mathrm{3}}{u}+\alpha\right)^{\mathrm{2}} }+\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\alpha^{\mathrm{3}} }\int\frac{{du}}{\sqrt{\mathrm{3}}{u}+\alpha}= \\ $$$$=−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}\alpha^{\mathrm{2}} }{u}^{−\mathrm{1}} −\frac{\mathrm{3}}{\alpha^{\mathrm{3}} }\mathrm{ln}\:{u}\:−\frac{\alpha^{\mathrm{2}} +\mathrm{3}}{\mathrm{2}\alpha^{\mathrm{2}} \left(\sqrt{\mathrm{3}}{u}+\alpha\right)}+\frac{\mathrm{3}}{\alpha^{\mathrm{3}} }\mathrm{ln}\:\left(\sqrt{\mathrm{3}}{u}+\alpha\right)\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\alpha^{\mathrm{2}} }\left({x}−\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right)−\frac{\mathrm{3}}{\alpha^{\mathrm{3}} }\mathrm{ln}\:\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right)\:−\frac{\alpha^{\mathrm{2}} +\mathrm{3}}{\mathrm{2}\alpha^{\mathrm{2}} \left({x}+\alpha+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right)}+\frac{\mathrm{3}}{\alpha^{\mathrm{3}} }\mathrm{ln}\:\left({x}+\alpha+\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right)\:+{C}= \\ $$$$=\frac{\mathrm{2}\alpha{x}^{\mathrm{2}} −\mathrm{6}{x}−\alpha\left(\alpha^{\mathrm{2}} +\mathrm{3}\right)−\mathrm{2}\left(\alpha{x}−\mathrm{3}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}}{\mathrm{2}\alpha^{\mathrm{2}} \left(\mathrm{2}\alpha{x}+\alpha^{\mathrm{2}} −\mathrm{3}\right)}+\frac{\mathrm{3}}{\alpha^{\mathrm{3}} }\mathrm{ln}\:\left(−\alpha{x}+\mathrm{3}+\alpha\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\right)\:+{C} \\ $$

Commented by mathmax by abdo last updated on 28/Sep/19

thank you sir mjs for this hardwork.

$${thank}\:{you}\:{sir}\:{mjs}\:{for}\:{this}\:{hardwork}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com