Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 69794 by mathmax by abdo last updated on 27/Sep/19

$$letp\left(x\right)={(x+1)}^6-e^{i\alpha }with\alpha real$$$$1)findtherootsofp\left(x\right)$$$$2)factorizep\left(x\right)insideC\left[x\right]$$$$3)factorizep\left(x\right)insideR\left[x\right]$$

Commented by mathmax by abdo last updated on 01/Oct/19

$$1)p\left(x\right)=0\iff {(x+1)}^6=e^{i\alpha }\iff \frac{{(x+1)}^6}{e^{i\alpha }}=1\iff \frac{{(x+1)}^6}{{\left(e^{\frac{i\alpha }{6}}\right)}^6}=1\Rightarrow$$$${\left((x+1)e^{-\frac{i\alpha }{6}}\right)}^6=e^{i2k\pi }\Rightarrow (x+1)e^{-\frac{i\alpha }{6}}=e^{\frac{i2k\pi }{6}}\Rightarrow$$$$(x+1)=e^{\frac{ik\pi }{3}}{e}^{\frac{i\alpha }{6}}\Rightarrow x+1=e^{\frac{i(2k\pi +\alpha )}{6}}\Rightarrow x=e^{i(\frac{2k\pi +\alpha )}{6}}-1$$$$sotherootsofp\left(x\right)are{z}_k=e^{i\left(\frac{2k\pi +\alpha }{6}\right)}-1withk\in \left[[0,5]\right]$$$$2)p\left(x\right)=a\prod _{k=0}^5(x-z_k)weseethata=1\Rightarrow$$$$p\left(x\right)=\prod _{k=0}^5(x+1-e^{i\left(\frac{3k\pi +\alpha }{6}\right)})$$

Commented by mathmax by abdo last updated on 01/Oct/19

$$erroroftypop\left(x\right)=\prod _{k=0}^5(x+1-e^{i\left(\frac{2k\pi +\alpha }{6}\right)})$$

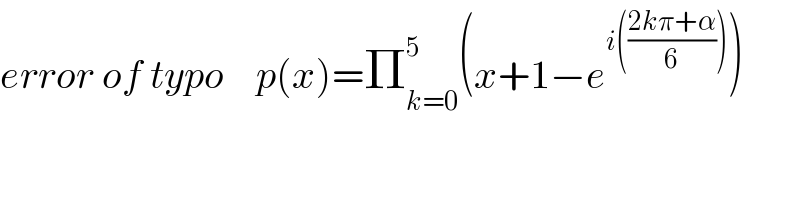
Answered by mind is power last updated on 29/Sep/19

$$p\left(x\right)=0\Rightarrow$$$${(x+1)}^6=e^{ia}\iff {(x+1)}^6=e^{i(a+2k\pi )}$$$$\Rightarrow x+1=e^{i(a+2k\pi )/6},k\in [0,5]$$$$\Rightarrow x_k=-1+e^{i\frac{a+2k\pi }{6}}$$$$2)p\left(x\right)=\underset{k=0}{\prod ^5}(x-(-1+e^{i\frac{a+2k\pi }{6}}))$$$$p\left(x\right)=\underset{k=0}{\prod ^5}(x+1-e^{i\frac{a+2k\pi }{6}})$$$$overIRnotpossibleonly[if{e}^{ia}\in IR\Rightarrow a=k\pi$$$$causep(-1)=-e^{ia}$$$$$$$$$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com