The acceleration of a particle moving in a straight line is defined as a=6t−20 m/s^2 , where t is in seconds. Knowing that s=0m when t=3s and that t=5sec when v=2m/s. Determine the total distance travelled when t=11s.


Question and Answers Forum

All Questions Topic List
Mechanics Questions
Previous in All Question Next in All Question
Previous in Mechanics Next in Mechanics
Question Number 69827 by Learner-123 last updated on 28/Sep/19

$T h e a c c e l e r a t i o n o f a p a r t i c l e m o v i n g$ $i n a s t r a i g h t l i n e i s d e f i n e d a s a = 6 t - 20$ $m / s^{2}, w h e r e t i s i n s e c o n d s . K n o w i n g$ $t h a t s = 0 m w h e n t = 3 s a n d t h a t t = 5 s e c$ $w h e n v = 2 m / s . D e t e r m i n e t h e t o t a l$ $d i s t a n c e t r a v e l l e d w h e n t = 11 s .$
	Answered by Rio Michael last updated on 28/Sep/19

	$v = \int a d t$ $= \int (6 t - 20) d t = 3 t^{2} - 20 t + c$ $v = 3 t^{2} - 20 t + c b u t t = 5, v = 2$ $2 = 5 - 100 + c$ $\Rightarrow c = 2 - 5 + 100$ $c = 97$ $\Rightarrow v = 3 t^{2} - 20 t + 97$ $s = \int v d t$ $= \int (3 t^{2} - 20 t + 97) d t$ $= t^{3} - 10 t^{2} + 97 t + c$ $s = 0 a t t = 3$ $s o l v e a n d s u b s t i t u d e f o r t = 11 s$
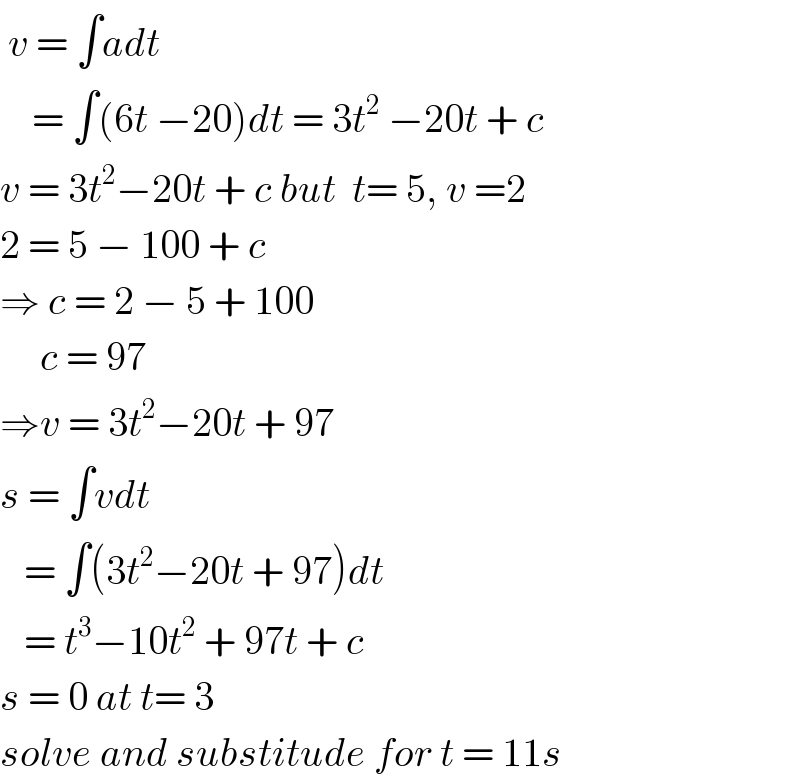
	Commented by Learner-123 last updated on 28/Sep/19

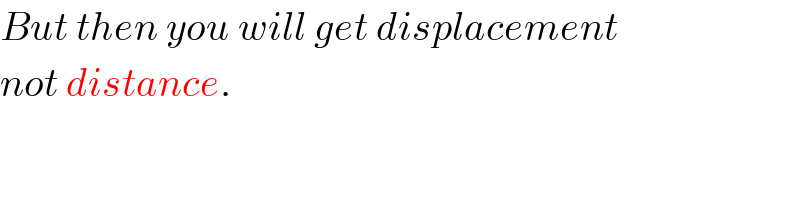
	$B u t t h e n y o u w i l l g e t d i s p l a c e m e n t$ $n o t d i s t a n c e .$
	Commented by Rio Michael last updated on 29/Sep/19

	$y e a h y o u r r i g h t$
	Answered by mr W last updated on 29/Sep/19

	$a = \frac{d v}{d t} = 6 t - 20$ $\int_{2}^{v} d v = \int_{5}^{t} (6 t - 20) d t$ $v - 2 = 3 t^{2} - 3 \times 5^{2} - 20 (t - 5)$ $\Rightarrow v = \frac{d s}{d t} = 3 t^{2} - 20 t + 27$ $\int_{0}^{s} d s = \int_{3}^{t} (3 t^{2} - 20 t + 27) d t$ $s = t^{3} - 3^{3} - 10 (t^{2} - 3^{2}) + 27 (t - 3)$ $\Rightarrow s = t^{3} - 10 t^{2} + 27 t - 18$ $a t t = 0 : s = - 18$ $a t t = 11 : s = 11^{3} - 10 \times 11^{2} + 27 \times 11 - 18 = 400$ $Δ s = 400 - (- 18) = 418 m$ $d i s t a n c e t r a v e l l e d = 418 m$
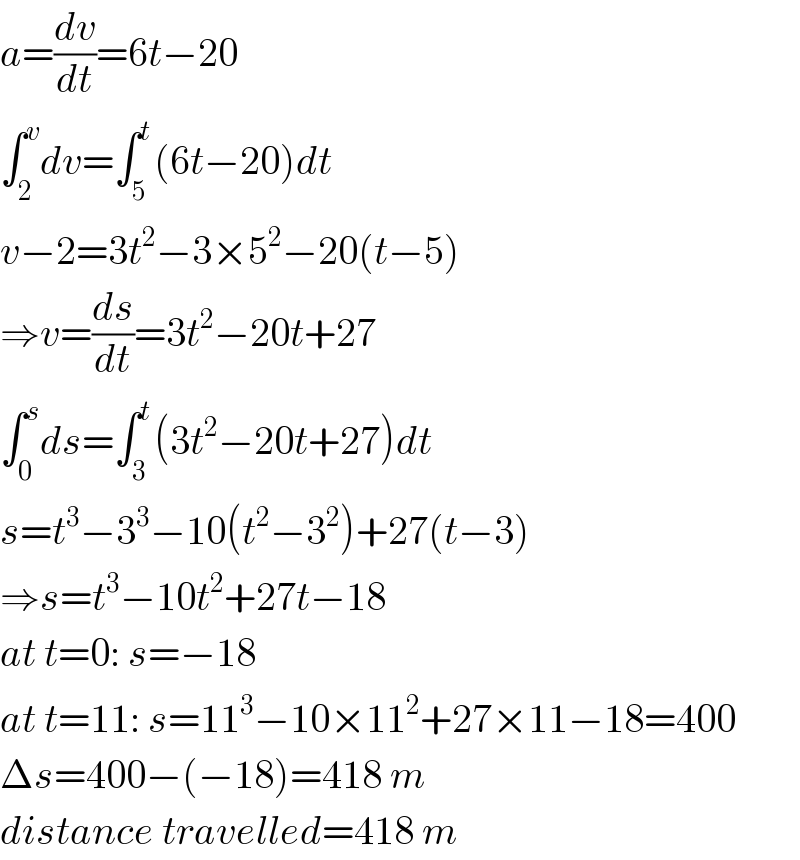
	Commented by Learner-123 last updated on 29/Sep/19

	$t h a n k s s i r .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum