
Question Number 6990 by Tawakalitu. last updated on 04/Aug/16

Answered by sou1618 last updated on 05/Aug/16
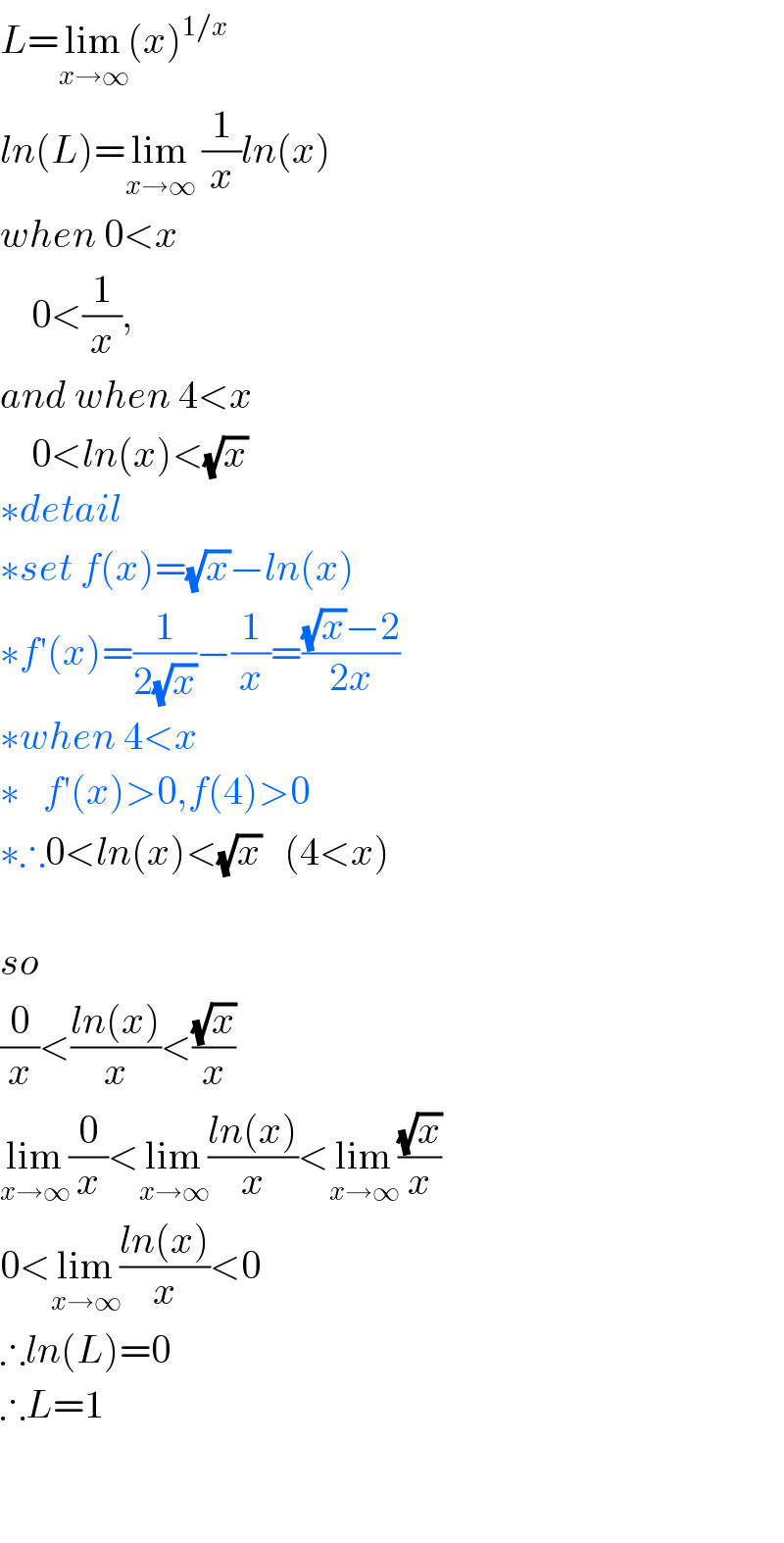
$${L}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left({x}\right)^{\mathrm{1}/{x}} \\ $$$${ln}\left({L}\right)=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{{x}}{ln}\left({x}\right) \\ $$$${when}\:\mathrm{0}<{x} \\ $$$$\:\:\:\:\mathrm{0}<\frac{\mathrm{1}}{{x}}, \\ $$$${and}\:{when}\:\mathrm{4}<{x} \\ $$$$\:\:\:\:\mathrm{0}<{ln}\left({x}\right)<\sqrt{{x}} \\ $$$$\ast{detail} \\ $$$$\ast{set}\:{f}\left({x}\right)=\sqrt{{x}}−{ln}\left({x}\right) \\ $$$$\ast{f}'\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{x}}}−\frac{\mathrm{1}}{{x}}=\frac{\sqrt{{x}}−\mathrm{2}}{\mathrm{2}{x}} \\ $$$$\ast{when}\:\mathrm{4}<{x} \\ $$$$\ast\:\:\:{f}'\left({x}\right)>\mathrm{0},{f}\left(\mathrm{4}\right)>\mathrm{0} \\ $$$$\ast\therefore\mathrm{0}<{ln}\left({x}\right)<\sqrt{{x}}\:\:\:\left(\mathrm{4}<{x}\right) \\ $$$$ \\ $$$${so} \\ $$$$\frac{\mathrm{0}}{{x}}<\frac{{ln}\left({x}\right)}{{x}}<\frac{\sqrt{{x}}}{{x}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{0}}{{x}}<\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{ln}\left({x}\right)}{{x}}<\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\sqrt{{x}}}{{x}} \\ $$$$\mathrm{0}<\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{ln}\left({x}\right)}{{x}}<\mathrm{0} \\ $$$$\therefore{ln}\left({L}\right)=\mathrm{0} \\ $$$$\therefore{L}=\mathrm{1} \\ $$$$ \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 05/Aug/16
$${I}\:{really}\:{appreciate}. \\ $$
