
Question and Answers Forum
Question Number 70025 by Tony Lin last updated on 30/Sep/19

Commented by mind is power last updated on 01/Oct/19
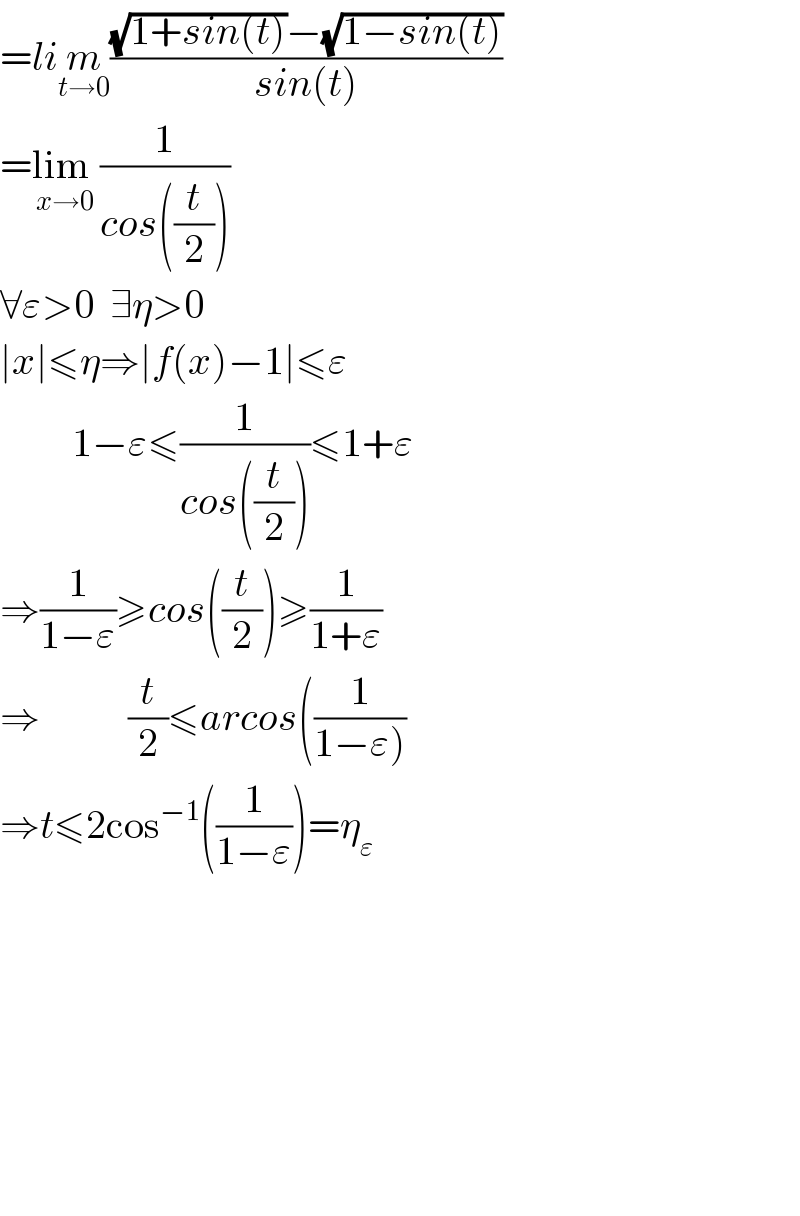
| ||
Question and Answers Forum | ||
Question Number 70025 by Tony Lin last updated on 30/Sep/19 | ||
 | ||
Commented by mind is power last updated on 01/Oct/19 | ||
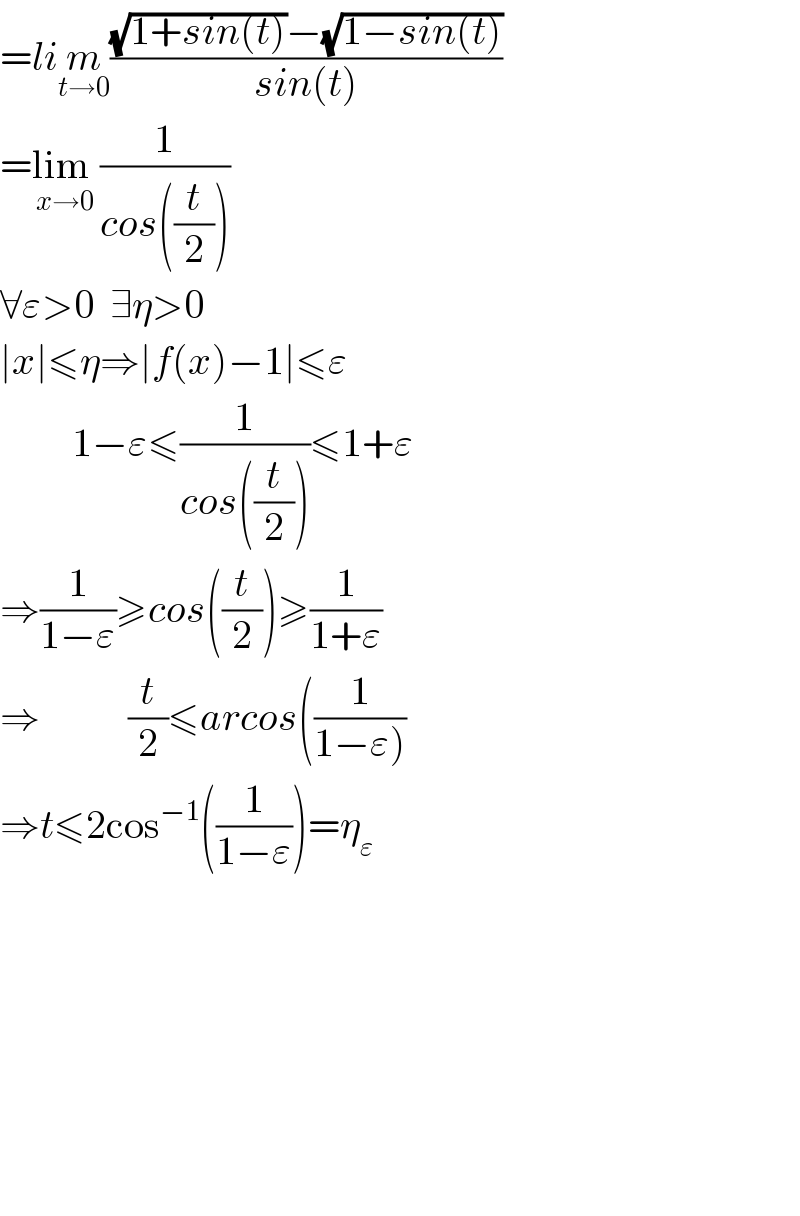 | ||