Question Number 70040 by Shamim last updated on 30/Sep/19
$$\mathrm{If},\:\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{b}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{c}^{\mathrm{3}} }\right)=\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} +\mathrm{c}^{\mathrm{3}} \:\mathrm{than} \\ $$$$\mathrm{prove}\:\mathrm{that}\:\mathrm{a},\mathrm{b},\mathrm{c}\:\mathrm{Successive}\:\mathrm{Proportional}. \\ $$
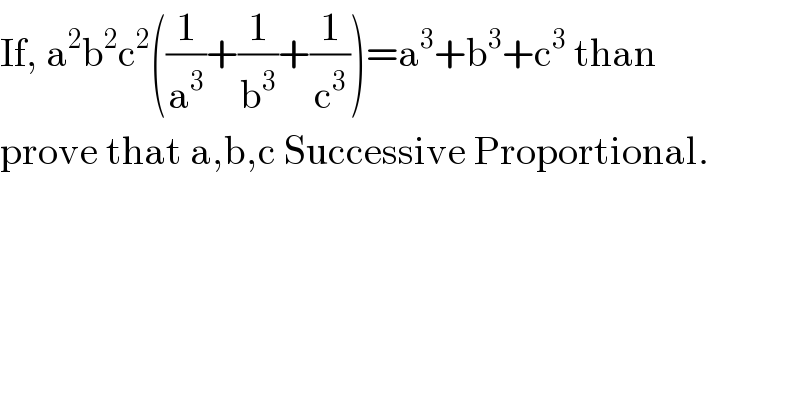
Commented by Prithwish sen last updated on 01/Oct/19
$$\left(\frac{\mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} }{\mathrm{a}}−\mathrm{a}^{\mathrm{3}} \right)+\left(\frac{\mathrm{a}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} }{\mathrm{b}}−\mathrm{b}^{\mathrm{3}} \right)+\left(\frac{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} }{\mathrm{c}}\:−\:\mathrm{c}^{\mathrm{3}} \right)=\mathrm{0} \\ $$$$\frac{\mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{4}} }{\mathrm{a}}\:+\frac{\mathrm{a}^{\mathrm{2}} \mathrm{b}^{\mathrm{2}} −\mathrm{c}^{\mathrm{4}} }{\mathrm{c}}\:+\left(\frac{\mathrm{a}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} −\mathrm{b}^{\mathrm{4}} }{\mathrm{c}}\right)=\mathrm{0} \\ $$$$\frac{\mathrm{b}^{\mathrm{2}} \mathrm{c}^{\mathrm{3}} −\mathrm{a}^{\mathrm{4}} \mathrm{c}\:+\:\mathrm{a}^{\mathrm{3}} \mathrm{b}^{\mathrm{2}} −\mathrm{ac}^{\mathrm{4}} }{\mathrm{ac}}\:+\frac{\mathrm{a}^{\mathrm{2}} \mathrm{c}^{\mathrm{2}} \:−\:\mathrm{b}^{\mathrm{4}} }{\mathrm{c}}\:=\:\mathrm{0} \\ $$$$\frac{\left(\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{ac}}\right)\left(\mathrm{a}^{\mathrm{3}} +\:\mathrm{c}^{\mathrm{3}} \right)}{\mathrm{ac}}\:−\:\frac{\left(\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{ac}}\right)\left(\mathrm{b}^{\mathrm{2}} +\mathrm{ac}\right)}{\mathrm{c}}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{b}^{\mathrm{2}} −\mathrm{ac}\right)\left(\frac{\mathrm{a}^{\mathrm{3}} +\mathrm{c}^{\mathrm{3}} }{\mathrm{ac}}\:−\:\frac{\mathrm{b}^{\mathrm{2}} +\mathrm{ac}}{\mathrm{c}}\:\right)=\mathrm{0} \\ $$$$\:\boldsymbol{\mathrm{considering}}\:\boldsymbol{\mathrm{only}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{b}}^{\mathrm{2}} −\boldsymbol{\mathrm{ac}}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}},\boldsymbol{\mathrm{c}}\:\boldsymbol{\mathrm{are}}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{proportion}}.\:\:\boldsymbol{\mathrm{proved}} \\ $$
Commented by Shamim last updated on 01/Oct/19
$$\mathrm{tnks} \\ $$
Commented by MJS last updated on 01/Oct/19
$$\mathrm{of}\:\mathrm{course}\:\mathrm{this}\:\mathrm{is}\:\mathrm{right} \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{saw}\:\mathrm{that}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{can}\:\mathrm{be} \\ $$$$\mathrm{transformed}\:\mathrm{to} \\ $$$${a}^{\mathrm{4}} {bc}+{ab}^{\mathrm{4}} {c}+{abc}^{\mathrm{4}} −{a}^{\mathrm{3}} {b}^{\mathrm{3}} −{a}^{\mathrm{3}} {c}^{\mathrm{3}} −{b}^{\mathrm{3}} {c}^{\mathrm{3}} =\mathrm{0}\:\Leftrightarrow \\ $$$$\Leftrightarrow\:\left({a}^{\mathrm{2}} −{bc}\right)\left({b}^{\mathrm{2}} −{ac}\right)\left({c}^{\mathrm{2}} −{ab}\right)=\mathrm{0} \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{thought}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{factorize} \\ $$$$ \\ $$$$\mathrm{on}\:\mathrm{the}\:\mathrm{other}\:\mathrm{hand}\:\mathrm{by}\:\mathrm{taking}\:\mathrm{the}\:\mathrm{result}\:\mathrm{and} \\ $$$$\mathrm{simply}\:\mathrm{putting}\:{b}={pa},\:{c}={p}^{\mathrm{2}} {a}\:\mathrm{or}\:\mathrm{just}\:{c}=\frac{{b}^{\mathrm{2}} }{{a}}\:\mathrm{we} \\ $$$$\mathrm{easily}\:\mathrm{find}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation}\:\mathrm{is}\:\mathrm{true} \\ $$$$ \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{thought}\:\mathrm{showing}\:\mathrm{that}\:\mathrm{with}\:{b}={pa}\:\mathrm{and} \\ $$$${c}={qa}\:\Rightarrow\:{q}={p}^{\mathrm{2}} \:\mathrm{is}\:\mathrm{more}\:\mathrm{convincing} \\ $$
Answered by MJS last updated on 30/Sep/19
![for a, b, c ∈R we can find p, q ∈R ⇒ b=pa∧c=qa a^2 b^2 c^2 ((1/a^3 )+(1/b^3 )+(1/c^3 ))=a^3 +b^3 +c^3 a^3 b^3 +a^3 c^3 +b^3 c^3 =a^4 bc+ab^4 c+abc^4 a^4 bc−a^3 (b^3 −c^3 )+a(b^4 c+bc^4 )−b^3 c^3 =0 b=pa∧c=qa, let a≤b≤c ⇒ 1≤p≤q a^6 (−p^3 q^3 +p^4 q+pq^4 −p^3 −q^3 +pq)=0 a≠0 −p^3 q^3 +p^4 q+pq^4 −p^3 −q^3 +pq=0 (p^2 −q)(p−q^2 )(pq−1)=0 ⇒ q=p^2 [∨q=±(√p)∨q=(1/p)] ⇒ ⟨a, b, c⟩=⟨a, pa, p^2 a⟩](Q70088.png)
$$\mathrm{for}\:{a},\:{b},\:{c}\:\in\mathbb{R}\:\mathrm{we}\:\mathrm{can}\:\mathrm{find}\:{p},\:{q}\:\in\mathbb{R}\:\Rightarrow\:{b}={pa}\wedge{c}={qa} \\ $$$$ \\ $$$${a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{a}^{\mathrm{3}} }+\frac{\mathrm{1}}{{b}^{\mathrm{3}} }+\frac{\mathrm{1}}{{c}^{\mathrm{3}} }\right)={a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} \\ $$$${a}^{\mathrm{3}} {b}^{\mathrm{3}} +{a}^{\mathrm{3}} {c}^{\mathrm{3}} +{b}^{\mathrm{3}} {c}^{\mathrm{3}} ={a}^{\mathrm{4}} {bc}+{ab}^{\mathrm{4}} {c}+{abc}^{\mathrm{4}} \\ $$$${a}^{\mathrm{4}} {bc}−{a}^{\mathrm{3}} \left({b}^{\mathrm{3}} −{c}^{\mathrm{3}} \right)+{a}\left({b}^{\mathrm{4}} {c}+{bc}^{\mathrm{4}} \right)−{b}^{\mathrm{3}} {c}^{\mathrm{3}} =\mathrm{0} \\ $$$${b}={pa}\wedge{c}={qa},\:\mathrm{let}\:{a}\leqslant{b}\leqslant{c}\:\Rightarrow\:\mathrm{1}\leqslant{p}\leqslant{q} \\ $$$${a}^{\mathrm{6}} \left(−{p}^{\mathrm{3}} {q}^{\mathrm{3}} +{p}^{\mathrm{4}} {q}+{pq}^{\mathrm{4}} −{p}^{\mathrm{3}} −{q}^{\mathrm{3}} +{pq}\right)=\mathrm{0} \\ $$$${a}\neq\mathrm{0} \\ $$$$−{p}^{\mathrm{3}} {q}^{\mathrm{3}} +{p}^{\mathrm{4}} {q}+{pq}^{\mathrm{4}} −{p}^{\mathrm{3}} −{q}^{\mathrm{3}} +{pq}=\mathrm{0} \\ $$$$\left({p}^{\mathrm{2}} −{q}\right)\left({p}−{q}^{\mathrm{2}} \right)\left({pq}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{q}={p}^{\mathrm{2}} \:\:\left[\vee{q}=\pm\sqrt{{p}}\vee{q}=\frac{\mathrm{1}}{{p}}\right] \\ $$$$\Rightarrow\:\langle{a},\:{b},\:{c}\rangle=\langle{a},\:{pa},\:{p}^{\mathrm{2}} {a}\rangle \\ $$
Commented by Shamim last updated on 30/Sep/19
$$\mathrm{It}'\mathrm{s}\:\mathrm{very}\:\mathrm{hard}.\:\mathrm{others}\:\mathrm{rule}??? \\ $$
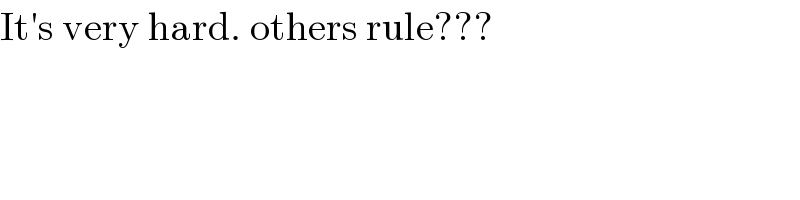
Commented by MJS last updated on 30/Sep/19
$$\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{that}\:\mathrm{hard}.\:\mathrm{write} \\ $$$$−{p}^{\mathrm{3}} {q}^{\mathrm{3}} +{p}^{\mathrm{4}} {q}+{pq}^{\mathrm{4}} −{p}^{\mathrm{3}} −{q}^{\mathrm{3}} +{pq}=\mathrm{0} \\ $$$$\mathrm{as} \\ $$$${pq}^{\mathrm{4}} −\left({p}^{\mathrm{3}} +\mathrm{1}\right){q}^{\mathrm{3}} +{p}\left({p}^{\mathrm{3}} +\mathrm{1}\right){q}−{p}^{\mathrm{3}} =\mathrm{0} \\ $$$$\mathrm{divide}\:\mathrm{by}\:{p} \\ $$$${q}^{\mathrm{4}} −\frac{{p}^{\mathrm{3}} +\mathrm{1}}{{p}}{q}^{\mathrm{3}} +\left({p}^{\mathrm{3}} +\mathrm{1}\right){q}−{p}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{know}\:\mathrm{if}\:\mathrm{there}'\mathrm{s}\:\mathrm{an}\:\mathrm{easy}\:\mathrm{solution}\:{q}_{\mathrm{1}} \:\Rightarrow \\ $$$${q}_{\mathrm{1}} \mid{p}^{\mathrm{2}} \:\Rightarrow\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{try}\:\pm\mathrm{1},\:\pm{p},\:\pm{p}^{\mathrm{2}} \\ $$$$\Rightarrow\:{q}_{\mathrm{1}} ={p}^{\mathrm{2}} \:\mathrm{and}\:\mathrm{this}\:\mathrm{is}\:\mathrm{enough}\:\mathrm{because}\:\mathrm{we} \\ $$$$\mathrm{set}\:{a}\leqslant{b}\leqslant{c}\:\Rightarrow\:\mathrm{1}\leqslant{p}\leqslant{q}\:\Rightarrow\:{q}\neq\pm\sqrt{{p}}\wedge{q}\neq\frac{\mathrm{1}}{{p}} \\ $$$$ \\ $$$$\mathrm{we}\:\mathrm{then}\:\mathrm{have} \\ $$$$\left({q}−{p}^{\mathrm{2}} \right)\left({q}^{\mathrm{3}} −\frac{\mathrm{1}}{{p}}{q}^{\mathrm{2}} −{pq}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{transform}\:\mathrm{to} \\ $$$$\left({q}−{p}^{\mathrm{2}} \right)\left({q}^{\mathrm{2}} \left({q}−\frac{\mathrm{1}}{{p}}\right)−{p}\left({q}−\frac{\mathrm{1}}{{p}}\right)\right)=\mathrm{0} \\ $$$$\Rightarrow\:{q}_{\mathrm{2}} =\frac{\mathrm{1}}{{p}} \\ $$$$\left({q}−{p}^{\mathrm{2}} \right)\left({q}−\frac{\mathrm{1}}{{p}}\right)\left({q}^{\mathrm{2}} −{p}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{q}_{\mathrm{3},\:\mathrm{4}} =\pm\sqrt{{p}} \\ $$