Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 70370 by Rasheed.Sindhi last updated on 04/Oct/19

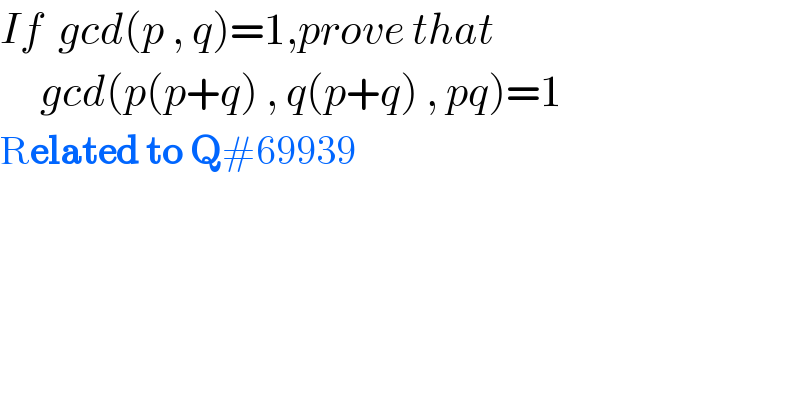
If gcd(p , q)=1,prove that gcd(p(p+q) , q(p+q) , pq)=1 Related to Q#69939

$${If}\:\:{gcd}\left({p}\:,\:{q}\right)=\mathrm{1},{prove}\:{that} \\ $$$$\:\:\:\:\:{gcd}\left({p}\left({p}+{q}\right)\:,\:{q}\left({p}+{q}\right)\:,\:{pq}\right)=\mathrm{1} \\ $$$$\mathrm{R}\boldsymbol{\mathrm{elated}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{Q}}#\mathrm{69939} \\ $$

Commented by mind is power last updated on 03/Oct/19

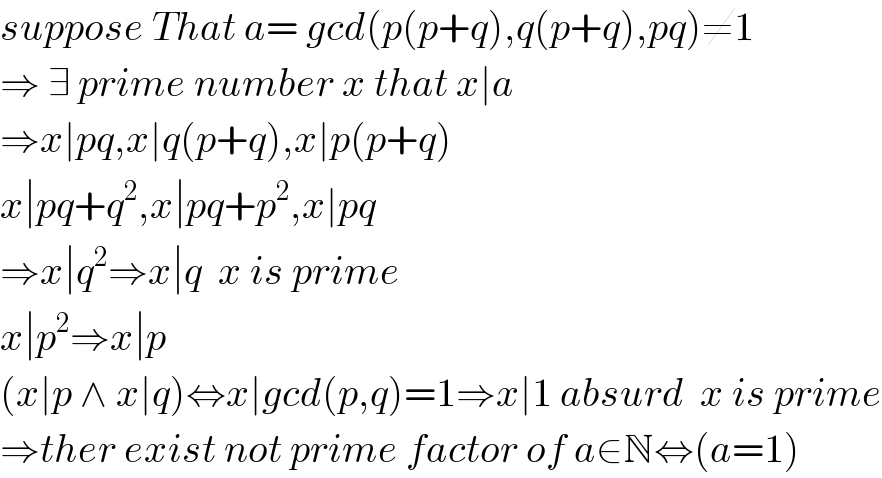
suppose That a= gcd(p(p+q),q(p+q),pq)≠1 ⇒ ∃ prime number x that x∣a ⇒x∣pq,x∣q(p+q),x∣p(p+q) x∣pq+q^2 ,x∣pq+p^2 ,x∣pq ⇒x∣q^2 ⇒x∣q x is prime x∣p^2 ⇒x∣p (x∣p ∧ x∣q)⇔x∣gcd(p,q)=1⇒x∣1 absurd x is prime ⇒ther exist not prime factor of a∈N⇔(a=1)

$${suppose}\:{That}\:{a}=\:{gcd}\left({p}\left({p}+{q}\right),{q}\left({p}+{q}\right),{pq}\right)\neq\mathrm{1} \\ $$$$\Rightarrow\:\exists\:{prime}\:{number}\:{x}\:{that}\:{x}\mid{a} \\ $$$$\Rightarrow{x}\mid{pq},{x}\mid{q}\left({p}+{q}\right),{x}\mid{p}\left({p}+{q}\right) \\ $$$${x}\mid{pq}+{q}^{\mathrm{2}} ,{x}\mid{pq}+{p}^{\mathrm{2}} ,{x}\mid{pq} \\ $$$$\Rightarrow{x}\mid{q}^{\mathrm{2}} \Rightarrow{x}\mid{q}\:\:{x}\:{is}\:{prime} \\ $$$${x}\mid{p}^{\mathrm{2}} \Rightarrow{x}\mid{p} \\ $$$$\left({x}\mid{p}\:\wedge\:{x}\mid{q}\right)\Leftrightarrow{x}\mid{gcd}\left({p},{q}\right)=\mathrm{1}\Rightarrow{x}\mid\mathrm{1}\:{absurd}\:\:{x}\:{is}\:{prime} \\ $$$$\Rightarrow{ther}\:{exist}\:{not}\:{prime}\:{factor}\:{of}\:{a}\in\mathbb{N}\Leftrightarrow\left({a}=\mathrm{1}\right) \\ $$

Commented by MJS last updated on 03/Oct/19

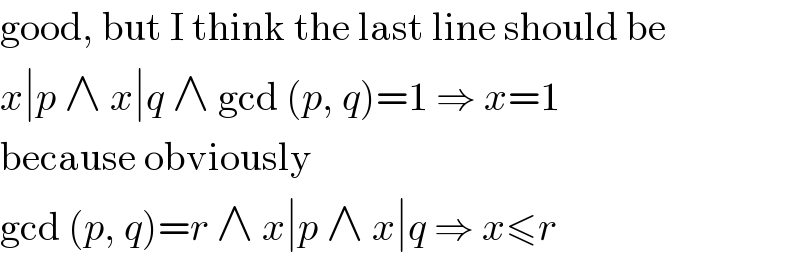
good, but I think the last line should be x∣p ∧ x∣q ∧ gcd (p, q)=1 ⇒ x=1 because obviously gcd (p, q)=r ∧ x∣p ∧ x∣q ⇒ x≤r

$$\mathrm{good},\:\mathrm{but}\:\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{last}\:\mathrm{line}\:\mathrm{should}\:\mathrm{be} \\ $$$${x}\mid{p}\:\wedge\:{x}\mid{q}\:\wedge\:\mathrm{gcd}\:\left({p},\:{q}\right)=\mathrm{1}\:\Rightarrow\:{x}=\mathrm{1} \\ $$$$\mathrm{because}\:\mathrm{obviously} \\ $$$$\mathrm{gcd}\:\left({p},\:{q}\right)={r}\:\wedge\:{x}\mid{p}\:\wedge\:{x}\mid{q}\:\Rightarrow\:{x}\leqslant{r} \\ $$

Commented by mind is power last updated on 03/Oct/19

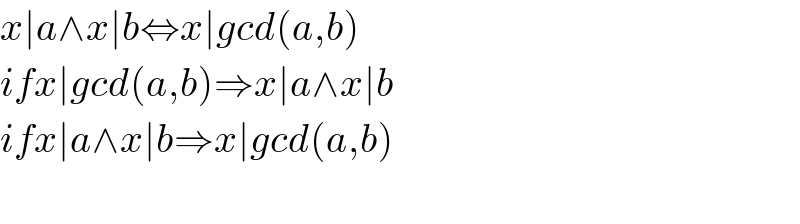
x∣a∧x∣b⇔x∣gcd(a,b) ifx∣gcd(a,b)⇒x∣a∧x∣b ifx∣a∧x∣b⇒x∣gcd(a,b)

$${x}\mid{a}\wedge{x}\mid{b}\Leftrightarrow{x}\mid{gcd}\left({a},{b}\right) \\ $$$${ifx}\mid{gcd}\left({a},{b}\right)\Rightarrow{x}\mid{a}\wedge{x}\mid{b} \\ $$$${ifx}\mid{a}\wedge{x}\mid{b}\Rightarrow{x}\mid{gcd}\left({a},{b}\right) \\ $$$$ \\ $$

Commented by Rasheed.Sindhi last updated on 04/Oct/19

Sir, Thanks & Appreciation→you!

$$\mathbb{S}\mathrm{ir},\:\mathbb{T}\mathrm{hanks}\:\&\:\mathbb{A}\mathrm{ppreciation}\rightarrow\mathrm{you}! \\ $$

Answered by $@ty@m123 last updated on 04/Oct/19

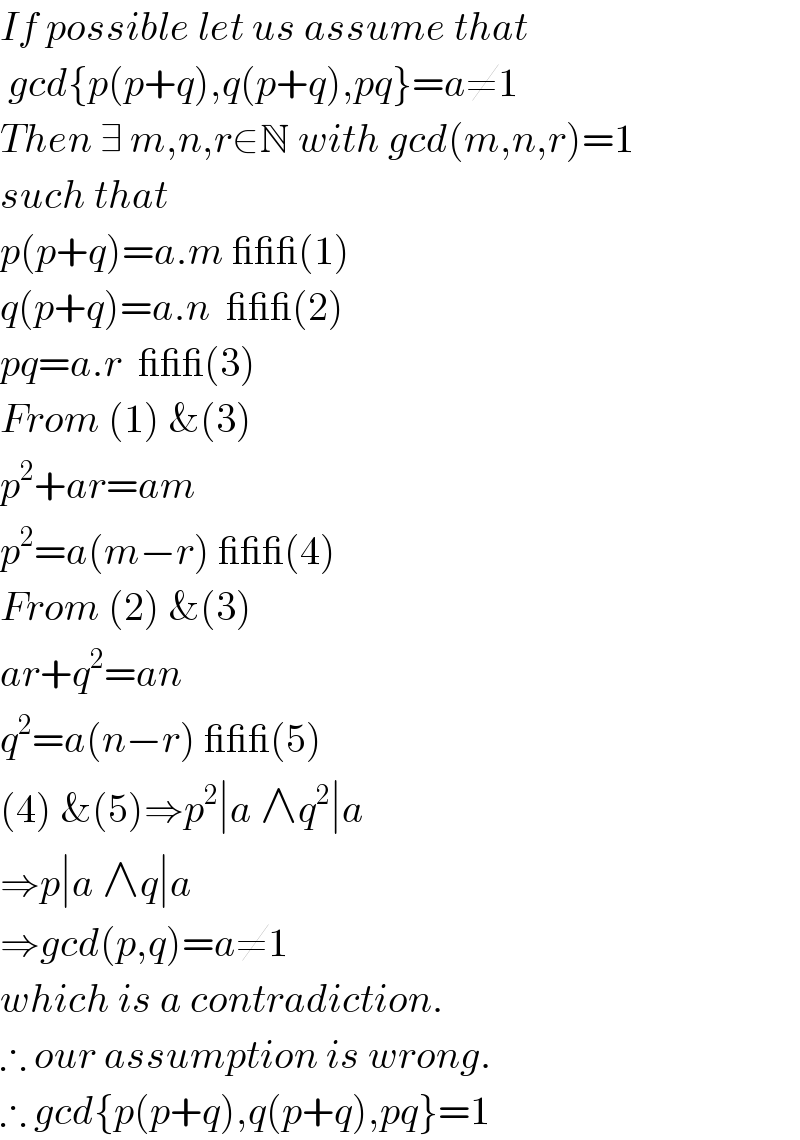
If possible let us assume that gcd{p(p+q),q(p+q),pq}=a≠1 Then ∃ m,n,r∈N with gcd(m,n,r)=1 such that p(p+q)=a.m ___(1) q(p+q)=a.n ___(2) pq=a.r ___(3) From (1) &(3) p^2 +ar=am p^2 =a(m−r) ___(4) From (2) &(3) ar+q^2 =an q^2 =a(n−r) ___(5) (4) &(5)⇒p^2 ∣a ∧q^2 ∣a ⇒p∣a ∧q∣a ⇒gcd(p,q)=a≠1 which is a contradiction. ∴ our assumption is wrong. ∴ gcd{p(p+q),q(p+q),pq}=1

$${If}\:{possible}\:{let}\:{us}\:{assume}\:{that} \\ $$$$\:{gcd}\left\{{p}\left({p}+{q}\right),{q}\left({p}+{q}\right),{pq}\right\}={a}\neq\mathrm{1} \\ $$$${Then}\:\exists\:{m},{n},{r}\in\mathbb{N}\:{with}\:{gcd}\left({m},{n},{r}\right)=\mathrm{1} \\ $$$${such}\:{that} \\ $$$${p}\left({p}+{q}\right)={a}.{m}\:\_\_\_\left(\mathrm{1}\right) \\ $$$${q}\left({p}+{q}\right)={a}.{n}\:\:\_\_\_\left(\mathrm{2}\right) \\ $$$${pq}={a}.{r}\:\:\_\_\_\left(\mathrm{3}\right) \\ $$$${From}\:\left(\mathrm{1}\right)\:\&\left(\mathrm{3}\right) \\ $$$${p}^{\mathrm{2}} +{ar}={am} \\ $$$${p}^{\mathrm{2}} ={a}\left({m}−{r}\right)\:\_\_\_\left(\mathrm{4}\right) \\ $$$${From}\:\left(\mathrm{2}\right)\:\&\left(\mathrm{3}\right) \\ $$$${ar}+{q}^{\mathrm{2}} ={an} \\ $$$${q}^{\mathrm{2}} ={a}\left({n}−{r}\right)\:\_\_\_\left(\mathrm{5}\right) \\ $$$$\left(\mathrm{4}\right)\:\&\left(\mathrm{5}\right)\Rightarrow{p}^{\mathrm{2}} \mid{a}\:\wedge{q}^{\mathrm{2}} \mid{a} \\ $$$$\Rightarrow{p}\mid{a}\:\wedge{q}\mid{a} \\ $$$$\Rightarrow{gcd}\left({p},{q}\right)={a}\neq\mathrm{1} \\ $$$${which}\:{is}\:{a}\:{contradiction}. \\ $$$$\therefore\:{our}\:{assumption}\:{is}\:{wrong}. \\ $$$$\therefore\:{gcd}\left\{{p}\left({p}+{q}\right),{q}\left({p}+{q}\right),{pq}\right\}=\mathrm{1} \\ $$

Commented by Rasheed.Sindhi last updated on 04/Oct/19

Thank you sir.I appriciate your approach!

$${Thank}\:{you}\:{sir}.{I}\:{appriciate}\:{your}\:{approach}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com