Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 70429 by TawaTawa last updated on 04/Oct/19

Commented by TawaTawa last updated on 04/Oct/19

If ABCD is a square, AH is the tangent of the sector BEF at G, AG:GH = 7, and DH = 2. Find the area of the square

Commented by MJS last updated on 04/Oct/19

AG:GH=7??? is it 1:7 or 7:1?

$${AG}:{GH}=\mathrm{7}??? \\ $$$$\mathrm{is}\:\mathrm{it}\:\mathrm{1}:\mathrm{7}\:\mathrm{or}\:\mathrm{7}:\mathrm{1}? \\ $$

Commented by TawaTawa last updated on 04/Oct/19

7:1 sir

$$\mathrm{7}:\mathrm{1}\:\:\mathrm{sir} \\ $$

Commented by MJS last updated on 04/Oct/19

ok but then the picture is wrong... it looks like 1:7

$$\mathrm{ok}\:\mathrm{but}\:\mathrm{then}\:\mathrm{the}\:\mathrm{picture}\:\mathrm{is}\:\mathrm{wrong}...\:\mathrm{it}\:\mathrm{looks} \\ $$$$\mathrm{like}\:\mathrm{1}:\mathrm{7} \\ $$

Commented by TawaTawa last updated on 04/Oct/19

Help me do it like 1:7 sir God bless you. Thanks for your time sir

$$\mathrm{Help}\:\mathrm{me}\:\mathrm{do}\:\mathrm{it}\:\mathrm{like}\:\:\:\mathrm{1}:\mathrm{7}\:\:\mathrm{sir} \\ $$$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}.\:\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir} \\ $$

Commented by MJS last updated on 04/Oct/19

will try with 7:1 later

$$\mathrm{will}\:\mathrm{try}\:\mathrm{with}\:\mathrm{7}:\mathrm{1}\:\mathrm{later} \\ $$

Answered by MJS last updated on 04/Oct/19

triangles HDA and AGB are similar AG^2 +GB^2 =BA^2 HD^2 +DA^2 =AH^2 AG=x; GH=7x; HD=2; BA=DA=s; GB=r x^2 +r^2 =s^2 4+s^2 =64x^2 ⇒ r^2 =((63)/(64))s^2 −(1/(16)) ((AG)/(HD))=((GB)/(DA))=((BA)/(AH)) (x/2)=(r/s)=(s/(8x)) ⇒ r=((√s^3 )/4) ⇒ (s^3 /(16))=((63)/(64))s^2 −(1/(16)) s^3 −((63)/4)s^2 +1=0 ⇒ s=−(1/4)∨s=8±2(√(15)) but s≥2 ⇒ s=8+2(√(15)) r=((7(√5))/2)+((9(√3))/2) x=((√5)/2)+((√3)/2) area=s^2 =124+32(√(15))

$$\mathrm{triangles}\:{HDA}\:\mathrm{and}\:{AGB}\:\mathrm{are}\:\mathrm{similar} \\ $$$${AG}^{\mathrm{2}} +{GB}^{\mathrm{2}} ={BA}^{\mathrm{2}} \\ $$$${HD}^{\mathrm{2}} +{DA}^{\mathrm{2}} ={AH}^{\mathrm{2}} \\ $$$${AG}={x};\:{GH}=\mathrm{7}{x};\:{HD}=\mathrm{2};\:{BA}={DA}={s};\:{GB}={r} \\ $$$$ \\ $$$${x}^{\mathrm{2}} +{r}^{\mathrm{2}} ={s}^{\mathrm{2}} \\ $$$$\mathrm{4}+{s}^{\mathrm{2}} =\mathrm{64}{x}^{\mathrm{2}} \\ $$$$\Rightarrow\:{r}^{\mathrm{2}} =\frac{\mathrm{63}}{\mathrm{64}}{s}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$ \\ $$$$\frac{{AG}}{{HD}}=\frac{{GB}}{{DA}}=\frac{{BA}}{{AH}} \\ $$$$\frac{{x}}{\mathrm{2}}=\frac{{r}}{{s}}=\frac{{s}}{\mathrm{8}{x}} \\ $$$$\Rightarrow\:{r}=\frac{\sqrt{{s}^{\mathrm{3}} }}{\mathrm{4}} \\ $$$$ \\ $$$$\Rightarrow\:\frac{{s}^{\mathrm{3}} }{\mathrm{16}}=\frac{\mathrm{63}}{\mathrm{64}}{s}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{16}} \\ $$$${s}^{\mathrm{3}} −\frac{\mathrm{63}}{\mathrm{4}}{s}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:{s}=−\frac{\mathrm{1}}{\mathrm{4}}\vee{s}=\mathrm{8}\pm\mathrm{2}\sqrt{\mathrm{15}} \\ $$$$\mathrm{but}\:{s}\geqslant\mathrm{2}\:\Rightarrow\:{s}=\mathrm{8}+\mathrm{2}\sqrt{\mathrm{15}} \\ $$$${r}=\frac{\mathrm{7}\sqrt{\mathrm{5}}}{\mathrm{2}}+\frac{\mathrm{9}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${x}=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${area}={s}^{\mathrm{2}} =\mathrm{124}+\mathrm{32}\sqrt{\mathrm{15}} \\ $$

Commented by TawaTawa last updated on 04/Oct/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by MJS last updated on 04/Oct/19

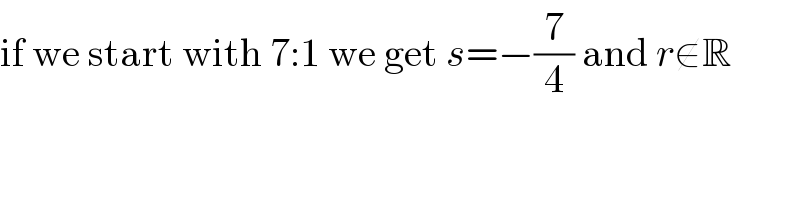
if we start with 7:1 we get s=−(7/4) and r∉R

$$\mathrm{if}\:\mathrm{we}\:\mathrm{start}\:\mathrm{with}\:\mathrm{7}:\mathrm{1}\:\mathrm{we}\:\mathrm{get}\:{s}=−\frac{\mathrm{7}}{\mathrm{4}}\:\mathrm{and}\:{r}\notin\mathbb{R} \\ $$

Commented by TawaTawa last updated on 04/Oct/19

Thanks for your time sir

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}\:\mathrm{sir} \\ $$

Commented by ajfour last updated on 04/Oct/19

⇒ r^2 =((63)/(64))s^2 −(7/(64)) i think r^2 =((63)/(64))s^2 −(4/(64)) Sir, this may account for the differnce.

$$\Rightarrow\:{r}^{\mathrm{2}} =\frac{\mathrm{63}}{\mathrm{64}}{s}^{\mathrm{2}} −\frac{\mathrm{7}}{\mathrm{64}} \\ $$$$\:\:\:{i}\:{think}\:\:\:\:{r}^{\mathrm{2}} =\frac{\mathrm{63}}{\mathrm{64}}{s}^{\mathrm{2}} −\frac{\mathrm{4}}{\mathrm{64}} \\ $$$$\:\:\:{Sir},\:{this}\:{may}\:{account}\:{for}\:{the} \\ $$$$\:\:\:{differnce}. \\ $$

Commented by MJS last updated on 04/Oct/19

you′re right, it′s a typo... thank you

$$\mathrm{you}'\mathrm{re}\:\mathrm{right},\:\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{typo}...\:\mathrm{thank}\:\mathrm{you} \\ $$

Answered by ajfour last updated on 04/Oct/19

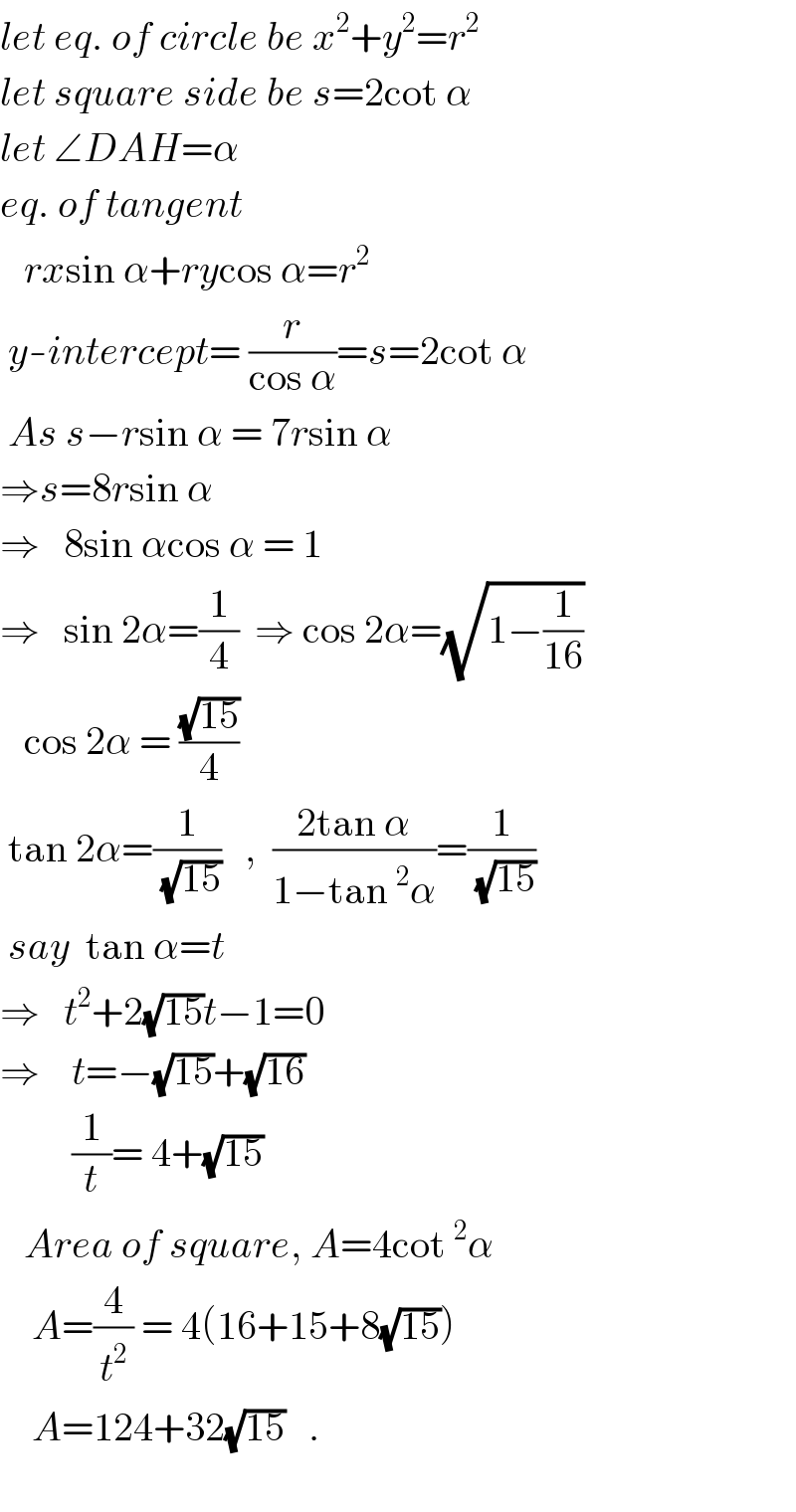
let eq. of circle be x^2 +y^2 =r^2 let square side be s=2cot α let ∠DAH=α eq. of tangent rxsin α+rycos α=r^2 y-intercept= (r/(cos α))=s=2cot α As s−rsin α = 7rsin α ⇒s=8rsin α ⇒ 8sin αcos α = 1 ⇒ sin 2α=(1/4) ⇒ cos 2α=(√(1−(1/(16)))) cos 2α = ((√(15))/4) tan 2α=(1/(√(15))) , ((2tan α)/(1−tan^2 α))=(1/(√(15))) say tan α=t ⇒ t^2 +2(√(15))t−1=0 ⇒ t=−(√(15))+(√(16)) (1/t)= 4+(√(15)) Area of square, A=4cot^2 α A=(4/t^2 ) = 4(16+15+8(√(15))) A=124+32(√(15)) .

$${let}\:{eq}.\:{of}\:{circle}\:{be}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${let}\:{square}\:{side}\:{be}\:{s}=\mathrm{2cot}\:\alpha \\ $$$${let}\:\angle{DAH}=\alpha \\ $$$${eq}.\:{of}\:{tangent}\:\: \\ $$$$\:\:\:{rx}\mathrm{sin}\:\alpha+{ry}\mathrm{cos}\:\alpha={r}^{\mathrm{2}} \\ $$$$\:{y}-{intercept}=\:\frac{{r}}{\mathrm{cos}\:\alpha}={s}=\mathrm{2cot}\:\alpha \\ $$$$\:{As}\:{s}−{r}\mathrm{sin}\:\alpha\:=\:\mathrm{7}{r}\mathrm{sin}\:\alpha \\ $$$$\Rightarrow{s}=\mathrm{8}{r}\mathrm{sin}\:\alpha \\ $$$$\Rightarrow\:\:\:\mathrm{8sin}\:\alpha\mathrm{cos}\:\alpha\:=\:\mathrm{1} \\ $$$$\Rightarrow\:\:\:\mathrm{sin}\:\mathrm{2}\alpha=\frac{\mathrm{1}}{\mathrm{4}}\:\:\Rightarrow\:\mathrm{cos}\:\mathrm{2}\alpha=\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{16}}} \\ $$$$\:\:\:\mathrm{cos}\:\mathrm{2}\alpha\:=\:\frac{\sqrt{\mathrm{15}}}{\mathrm{4}} \\ $$$$\:\mathrm{tan}\:\mathrm{2}\alpha=\frac{\mathrm{1}}{\sqrt{\mathrm{15}}}\:\:\:,\:\:\frac{\mathrm{2tan}\:\alpha}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \alpha}=\frac{\mathrm{1}}{\sqrt{\mathrm{15}}} \\ $$$$\:{say}\:\:\mathrm{tan}\:\alpha={t} \\ $$$$\Rightarrow\:\:\:{t}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{15}}{t}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:{t}=−\sqrt{\mathrm{15}}+\sqrt{\mathrm{16}} \\ $$$$\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{t}}=\:\mathrm{4}+\sqrt{\mathrm{15}} \\ $$$$\:\:\:{Area}\:{of}\:{square},\:{A}=\mathrm{4cot}\:^{\mathrm{2}} \alpha \\ $$$$\:\:\:\:{A}=\frac{\mathrm{4}}{{t}^{\mathrm{2}} }\:=\:\mathrm{4}\left(\mathrm{16}+\mathrm{15}+\mathrm{8}\sqrt{\mathrm{15}}\right) \\ $$$$\:\:\:\:{A}=\mathrm{124}+\mathrm{32}\sqrt{\mathrm{15}}\:\:\:. \\ $$$$\:\: \\ $$

Commented by TawaTawa last updated on 04/Oct/19

God bless you sir

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by MJS last updated on 04/Oct/19

(√(124+32(√(15))))=8+2(√(15))≈15.74596... why do we get different solutions?

$$\sqrt{\mathrm{124}+\mathrm{32}\sqrt{\mathrm{15}}}=\mathrm{8}+\mathrm{2}\sqrt{\mathrm{15}}\approx\mathrm{15}.\mathrm{74596}... \\ $$$$\mathrm{why}\:\mathrm{do}\:\mathrm{we}\:\mathrm{get}\:\mathrm{different}\:\mathrm{solutions}? \\ $$

Answered by Henri Boucatchou last updated on 05/Oct/19

What′s happening here, people text pictures without any question??

$$\boldsymbol{{What}}'\boldsymbol{{s}}\:\:\boldsymbol{{happening}}\:\:\boldsymbol{{here}},\:\:\boldsymbol{{people}}\:\:\boldsymbol{{text}}\:\:\boldsymbol{{pictures}}\:\:\boldsymbol{{without}}\:\:\boldsymbol{{any}}\:\:\boldsymbol{{question}}?? \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com