Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 70483 by Mikaell last updated on 04/Oct/19

$$\int \frac{ln2x}{ln4x}.\frac{dx}{x}$$

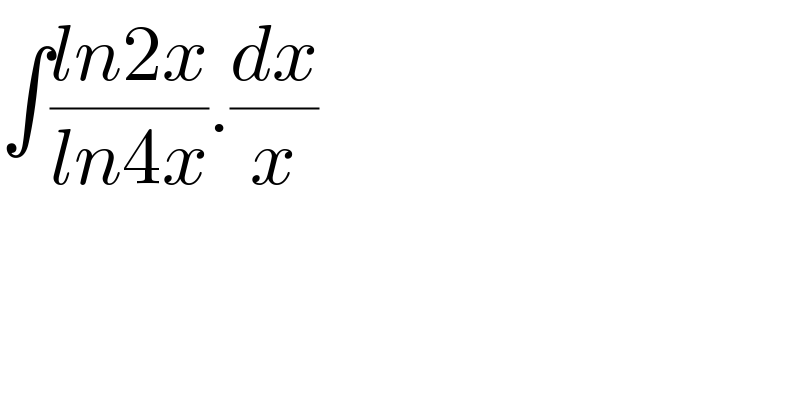
Commented by peter frank last updated on 04/Oct/19

$$thankx$$

Commented by kaivan.ahmadi last updated on 04/Oct/19

$$u=lnx\Rightarrow du=\frac{dx}{x}$$$$ln2x=ln2+lnx=u+ln2$$$$ln4x=ln4+lnx=u+ln4$$$$\Rightarrow \int \frac{u+ln2}{u+ln4}du=\int \frac{udu}{u+ln4}+\int \frac{ln2du}{u+ln4}=$$$$\int (1-\frac{ln4}{u+ln4})du+ln2\int \frac{du}{u+ln4}=$$$$u-ln4ln(u+ln4)+ln2ln(u+ln4)+C=$$$$u+(ln2-ln4)ln(u+ln4)+C=$$$$u-ln2ln(u+ln4)+C=lnx-ln2ln(lnx+ln4)+C=$$$$lnx-ln2ln\left(ln4x\right)+C$$$$$$$$$$

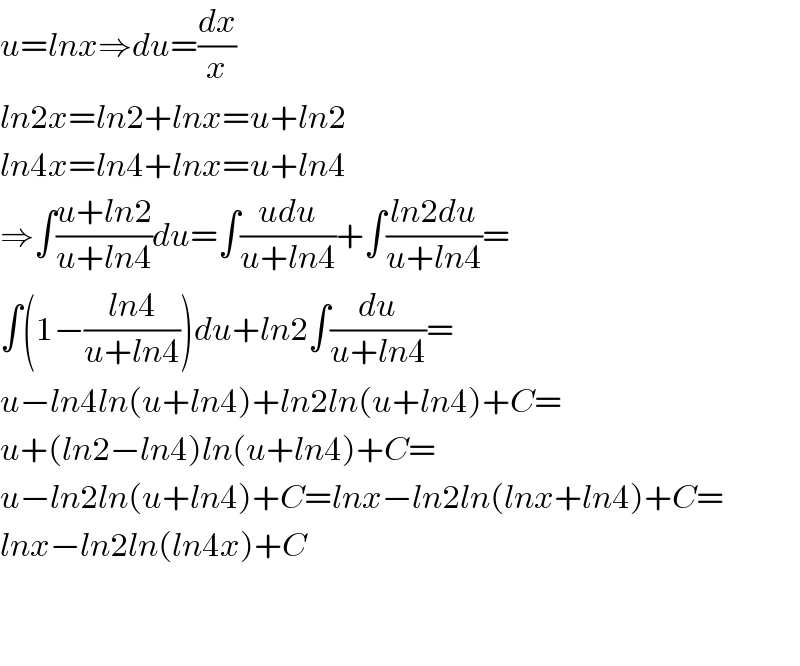
Commented by Mikaell last updated on 04/Oct/19

$$thankyouSir$$

Answered by Tanmay chaudhury last updated on 04/Oct/19

$$lnx=t\to \frac{dt}{dx}=\frac{1}{x}$$$$\int \frac{ln2+lnx}{2ln2+lnx}\times \frac{dx}{x}$$$$\int \frac{ln2+t}{2ln2+t}\times dt$$$$\frac{1}{4}\int \frac{2ln2+t+t}{2ln2+t}dt$$$$\frac{1}{4}\int dt+\frac{1}{4}\int \frac{2ln2+t-2ln2}{2ln2+t}dt$$$$\frac{1}{2}\int dt-\frac{ln2}{2}\int \frac{dt}{2ln2+t}$$$$\frac{t}{2}-\frac{ln2}{2}ln(2ln2+t)+C$$$$\frac{lnx}{2}-\frac{ln2}{2}ln(2ln2+lnx)+c$$

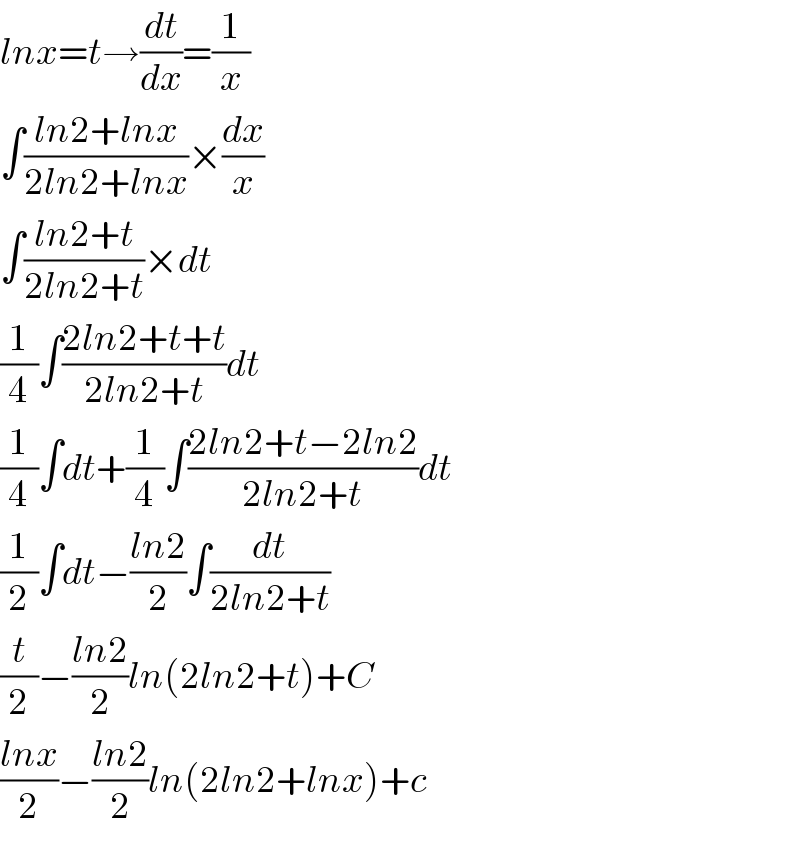
Commented by peter frank last updated on 04/Oct/19

$$thanx$$

Commented by Mikaell last updated on 04/Oct/19

$$thankyouSir$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com