Question and Answers Forum

All Questions      Topic List

Differential Equation Questions

Previous in All Question      Next in All Question      

Previous in Differential Equation      Next in Differential Equation      

Question Number 70720 by oyemi kemewari last updated on 07/Oct/19

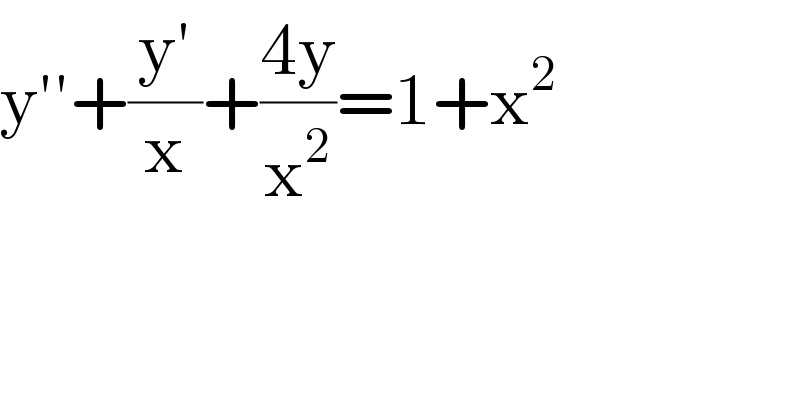
y′′+((y′)/x)+((4y)/x^2 )=1+x^2

$$\mathrm{y}''+\frac{\mathrm{y}'}{\mathrm{x}}+\frac{\mathrm{4y}}{\mathrm{x}^{\mathrm{2}} }=\mathrm{1}+\mathrm{x}^{\mathrm{2}} \\ $$

Commented by Rasheed.Sindhi last updated on 07/Oct/19

Thank you!

$$\mathcal{T}{hank}\:{you}! \\ $$

Commented by Rasheed.Sindhi last updated on 07/Oct/19

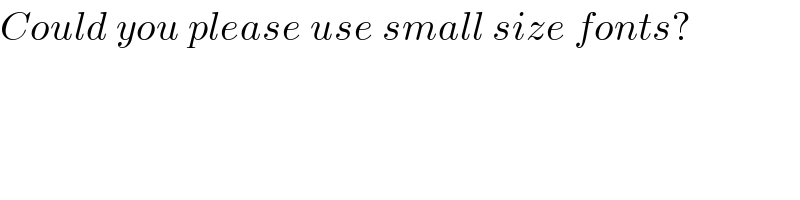
Could you please use small size fonts?

$${Could}\:{you}\:{please}\:{use}\:{small}\:{size}\:{fonts}? \\ $$

Commented by oyemi kemewari last updated on 07/Oct/19

ok sir

Commented by mind is power last updated on 07/Oct/19

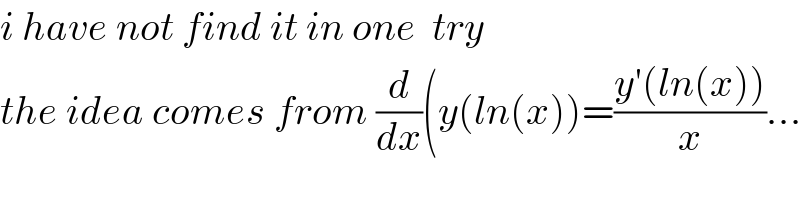
i have not find it in one try the idea comes from (d/dx)(y(ln(x))=((y′(ln(x)))/x)...

$${i}\:{have}\:{not}\:{find}\:{it}\:{in}\:{one}\:\:{try}\: \\ $$$${the}\:{idea}\:{comes}\:{from}\:\frac{{d}}{{dx}}\left({y}\left({ln}\left({x}\right)\right)=\frac{{y}'\left({ln}\left({x}\right)\right)}{{x}}...\right. \\ $$

Answered by mind is power last updated on 07/Oct/19

⇔x^2 y′′+xy′+4y=x^2 (1+x^2 ) ∀x∈R^∗ ...E let t=ln(x), y(x)=g(t) ,x=e^t (dy/dx)=(dy/dt).(dt/dx)=g′(t).((dx/dt))^(−1) =e^(−t) g′(t) (d^2 y/dx^2 )=(d/dx)((dy/dx))=(dt/dx).(d/dt)(e^(−t) g′(t))=((dx/dt))^(−1) .(−e^(−t) g′(t)+e^(−t) g′′(t)) =e^(−t) .(−e^(−t) g′(t)+e^(−t) g′′(t))=−e^(−2t) g′(t)+e^(−2t) g′′(t) E⇔e^(2t) (−e^(−2t) g′(t)+e^(−2t) g′′(t))+e^t (e^(−t) g′(t))+4g(t)=e^(2t) (1+e^(2t) ) ⇔−g′(t)+g′′(t)+g′(t)+4g(t)=e^(2t) +e^(4t) ⇒g′′(t)+4g(t)=e^(2t) +e^(4t) easy too solve from hear Homogenious EQ g′′+4g=0⇔g(t)=acos(2t)+bsin(2t),a,b∈R particular solution let g_0 =ae^(2t) +ce^(4t) ⇒4ae^(2t) +16ce^(4t) +4ae^(2t) +4ce^(4t) =e^(2t) +e^(4t) ⇒a=(1/8),c=(1/(20)) g(t)=acos(2t)+bsin(2t)+(e^(2t) /8)+(e^(4t) /(20)) y(x)=g(t)=g(ln(x)) Y(x)=acos(2ln(x))+bsin(2ln(x))+(e^(2ln(x)) /8)+(e^(4ln(x)) /(20)) Y(x)=acos(2ln(x))+bsin(2ln(x))+(x^2 /8)+(x^4 /(20))

$$\Leftrightarrow{x}^{\mathrm{2}} {y}''+{xy}'+\mathrm{4}{y}={x}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)\:\:\:\forall{x}\in\mathbb{R}^{\ast} ...{E} \\ $$$${let}\:{t}={ln}\left({x}\right),\:{y}\left({x}\right)={g}\left({t}\right)\:\:,{x}={e}^{{t}} \\ $$$$\frac{{dy}}{{dx}}=\frac{{dy}}{{dt}}.\frac{{dt}}{{dx}}={g}'\left({t}\right).\left(\frac{{dx}}{{dt}}\right)^{−\mathrm{1}} ={e}^{−{t}} {g}'\left({t}\right) \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{{d}}{{dx}}\left(\frac{{dy}}{{dx}}\right)=\frac{{dt}}{{dx}}.\frac{{d}}{{dt}}\left({e}^{−{t}} {g}'\left({t}\right)\right)=\left(\frac{{dx}}{{dt}}\right)^{−\mathrm{1}} .\left(−{e}^{−{t}} {g}'\left({t}\right)+{e}^{−{t}} {g}''\left({t}\right)\right) \\ $$$$={e}^{−{t}} .\left(−{e}^{−{t}} {g}'\left({t}\right)+{e}^{−{t}} {g}''\left({t}\right)\right)=−{e}^{−\mathrm{2}{t}} {g}'\left({t}\right)+{e}^{−\mathrm{2}{t}} {g}''\left({t}\right) \\ $$$${E}\Leftrightarrow{e}^{\mathrm{2}{t}} \left(−{e}^{−\mathrm{2}{t}} {g}'\left({t}\right)+{e}^{−\mathrm{2}{t}} {g}''\left({t}\right)\right)+{e}^{{t}} \left({e}^{−{t}} {g}'\left({t}\right)\right)+\mathrm{4}{g}\left({t}\right)={e}^{\mathrm{2}{t}} \left(\mathrm{1}+{e}^{\mathrm{2}{t}} \right) \\ $$$$\Leftrightarrow−{g}'\left({t}\right)+{g}''\left({t}\right)+{g}'\left({t}\right)+\mathrm{4}{g}\left({t}\right)={e}^{\mathrm{2}{t}} +{e}^{\mathrm{4}{t}} \\ $$$$\Rightarrow{g}''\left({t}\right)+\mathrm{4}{g}\left({t}\right)={e}^{\mathrm{2}{t}} +{e}^{\mathrm{4}{t}} \\ $$$${easy}\:{too}\:{solve}\:{from}\:{hear} \\ $$$${Homogenious}\:{EQ} \\ $$$${g}''+\mathrm{4}{g}=\mathrm{0}\Leftrightarrow{g}\left({t}\right)={acos}\left(\mathrm{2}{t}\right)+{bsin}\left(\mathrm{2}{t}\right),{a},{b}\in\mathbb{R} \\ $$$${particular}\:{solution}\: \\ $$$${let}\:{g}_{\mathrm{0}} ={ae}^{\mathrm{2}{t}} +{ce}^{\mathrm{4}{t}} \\ $$$$\Rightarrow\mathrm{4}{ae}^{\mathrm{2}{t}} +\mathrm{16}{ce}^{\mathrm{4}{t}} +\mathrm{4}{ae}^{\mathrm{2}{t}} +\mathrm{4}{ce}^{\mathrm{4}{t}} ={e}^{\mathrm{2}{t}} +{e}^{\mathrm{4}{t}} \\ $$$$\Rightarrow{a}=\frac{\mathrm{1}}{\mathrm{8}},{c}=\frac{\mathrm{1}}{\mathrm{20}} \\ $$$${g}\left({t}\right)={acos}\left(\mathrm{2}{t}\right)+{bsin}\left(\mathrm{2}{t}\right)+\frac{{e}^{\mathrm{2}{t}} }{\mathrm{8}}+\frac{{e}^{\mathrm{4}{t}} }{\mathrm{20}} \\ $$$${y}\left({x}\right)={g}\left({t}\right)={g}\left({ln}\left({x}\right)\right) \\ $$$${Y}\left({x}\right)={acos}\left(\mathrm{2}{ln}\left({x}\right)\right)+{bsin}\left(\mathrm{2}{ln}\left({x}\right)\right)+\frac{{e}^{\mathrm{2}{ln}\left({x}\right)} }{\mathrm{8}}+\frac{{e}^{\mathrm{4}{ln}\left({x}\right)} }{\mathrm{20}} \\ $$$${Y}\left({x}\right)={acos}\left(\mathrm{2}{ln}\left({x}\right)\right)+{bsin}\left(\mathrm{2}{ln}\left({x}\right)\right)+\frac{{x}^{\mathrm{2}} }{\mathrm{8}}+\frac{{x}^{\mathrm{4}} }{\mathrm{20}} \\ $$$$ \\ $$$$ \\ $$

Commented by oyemi kemewari last updated on 07/Oct/19

thank you sir

Commented by mind is power last updated on 07/Oct/19

y′re Welcom

$${y}'{re}\:{Welcom} \\ $$

Answered by Joel122 last updated on 08/Oct/19

y′′ + ((1/x))y′ + ((4/x^2 ))y = 1 + x^2 x^2 y′′ + xy′ + 4y = x^2 + x^4 ... (i) • Homogeneous solution x^2 y′′ + xy′ + 4y = 0 → Euler−Cauchy eq. Let y(x) = x^m be the solution. Then, x^m [(m^2 − m) + m + 4] = 0 ⇒ m^2 + 4 = 0 ⇒ m_1 = 2i, m_2 = −2i ⇒ y_h (x) = C_1 x^(2i) + C_2 x^(−2i) = α cos (ln x^2 ) + β sin (ln x^2 ) • Particular solution Using method of undetermined parameter, we have y_p (x) = Ax^4 + Bx^3 + Cx^2 + Dx + E y_p ^′ (x) = 4Ax^3 + 3Bx^2 + 2Cx + D y_p ^(′′) (x) = 12Ax^2 + 6Bx + 2C Plugging these equations to (i) x^2 [12Ax^2 + 6Bx + 2C] + x[4Ax^3 + 3Bx^2 + 2Cx + D] + 4[Ax^4 + Bx^3 + Cx^2 + Dx + E] = x^2 + x^4 ⇒ 20Ax^4 + 13Bx^3 + 8Cx^2 + 5Dx + 4E = x^4 + x^2 By comparing the coefficients, we have A = (1/(20)), B = 0, C = (1/8), D = 0, E = 0 ⇒ y_p (x) = (x^4 /(20)) + (x^2 /8) ∴ y(x) = y_h (x) + y_p (x)

$${y}''\:+\:\left(\frac{\mathrm{1}}{{x}}\right){y}'\:+\:\left(\frac{\mathrm{4}}{{x}^{\mathrm{2}} }\right){y}\:=\:\mathrm{1}\:+\:{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} {y}''\:+\:{xy}'\:+\:\mathrm{4}{y}\:=\:{x}^{\mathrm{2}} \:+\:{x}^{\mathrm{4}} \:\:\:\:\:\:\:\:...\:\left({i}\right) \\ $$$$ \\ $$$$\bullet\:\mathrm{Homogeneous}\:\mathrm{solution} \\ $$$${x}^{\mathrm{2}} {y}''\:+\:{xy}'\:+\:\mathrm{4}{y}\:=\:\mathrm{0}\:\:\rightarrow\:\:\mathrm{Euler}−\mathrm{Cauchy}\:\mathrm{eq}. \\ $$$$\mathrm{Let}\:{y}\left({x}\right)\:=\:{x}^{{m}} \:\mathrm{be}\:\mathrm{the}\:\mathrm{solution}.\:\mathrm{Then}, \\ $$$${x}^{{m}} \left[\left({m}^{\mathrm{2}} \:−\:{m}\right)\:+\:{m}\:+\:\mathrm{4}\right]\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{m}^{\mathrm{2}} \:+\:\mathrm{4}\:=\:\mathrm{0}\:\Rightarrow\:{m}_{\mathrm{1}} \:=\:\mathrm{2}{i},\:{m}_{\mathrm{2}} \:=\:−\mathrm{2}{i} \\ $$$$\Rightarrow\:{y}_{{h}} \left({x}\right)\:=\:{C}_{\mathrm{1}} {x}^{\mathrm{2}{i}} \:+\:{C}_{\mathrm{2}} {x}^{−\mathrm{2}{i}} \:=\:\alpha\:\mathrm{cos}\:\left(\mathrm{ln}\:{x}^{\mathrm{2}} \right)\:+\:\beta\:\mathrm{sin}\:\left(\mathrm{ln}\:{x}^{\mathrm{2}} \right)\: \\ $$$$ \\ $$$$\bullet\:\mathrm{Particular}\:\mathrm{solution} \\ $$$$\mathrm{Using}\:\mathrm{method}\:\mathrm{of}\:\mathrm{undetermined}\:\mathrm{parameter},\:\mathrm{we}\:\mathrm{have} \\ $$$${y}_{{p}} \left({x}\right)\:=\:{Ax}^{\mathrm{4}} \:+\:{Bx}^{\mathrm{3}} \:+\:{Cx}^{\mathrm{2}} \:+\:{Dx}\:+\:{E} \\ $$$${y}_{{p}} ^{'} \left({x}\right)\:=\:\mathrm{4}{Ax}^{\mathrm{3}} \:+\:\mathrm{3}{Bx}^{\mathrm{2}} \:+\:\mathrm{2}{Cx}\:+\:{D} \\ $$$${y}_{{p}} ^{''} \left({x}\right)\:=\:\mathrm{12}{Ax}^{\mathrm{2}} \:+\:\mathrm{6}{Bx}\:+\:\mathrm{2}{C} \\ $$$$\mathrm{Plugging}\:\mathrm{these}\:\mathrm{equations}\:\mathrm{to}\:\left({i}\right) \\ $$$${x}^{\mathrm{2}} \left[\mathrm{12}{Ax}^{\mathrm{2}} \:+\:\mathrm{6}{Bx}\:+\:\mathrm{2}{C}\right]\:+\:{x}\left[\mathrm{4}{Ax}^{\mathrm{3}} \:+\:\mathrm{3}{Bx}^{\mathrm{2}} \:+\:\mathrm{2}{Cx}\:+\:{D}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\mathrm{4}\left[{Ax}^{\mathrm{4}} \:+\:{Bx}^{\mathrm{3}} \:+\:{Cx}^{\mathrm{2}} \:+\:{Dx}\:+\:{E}\right]\:=\:{x}^{\mathrm{2}} \:+\:{x}^{\mathrm{4}} \\ $$$$\Rightarrow\:\mathrm{20}{Ax}^{\mathrm{4}} \:+\:\mathrm{13}{Bx}^{\mathrm{3}} \:+\:\mathrm{8}{Cx}^{\mathrm{2}} \:+\:\mathrm{5}{Dx}\:+\:\mathrm{4}{E}\:=\:{x}^{\mathrm{4}} \:+\:{x}^{\mathrm{2}} \\ $$$$\mathrm{By}\:\mathrm{comparing}\:\mathrm{the}\:\mathrm{coefficients},\:\mathrm{we}\:\mathrm{have} \\ $$$${A}\:=\:\frac{\mathrm{1}}{\mathrm{20}},\:{B}\:=\:\mathrm{0},\:{C}\:=\:\frac{\mathrm{1}}{\mathrm{8}},\:{D}\:=\:\mathrm{0},\:{E}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:{y}_{{p}} \left({x}\right)\:=\:\frac{{x}^{\mathrm{4}} }{\mathrm{20}}\:+\:\frac{{x}^{\mathrm{2}} }{\mathrm{8}} \\ $$$$ \\ $$$$\therefore\:{y}\left({x}\right)\:=\:{y}_{{h}} \left({x}\right)\:+\:{y}_{{p}} \left({x}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com