
Question and Answers Forum
Question Number 70818 by oyemi kemewari last updated on 08/Oct/19
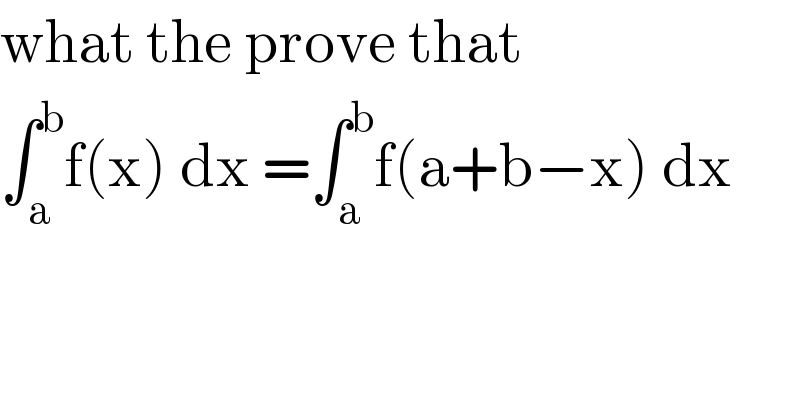
Commented by kaivan.ahmadi last updated on 08/Oct/19
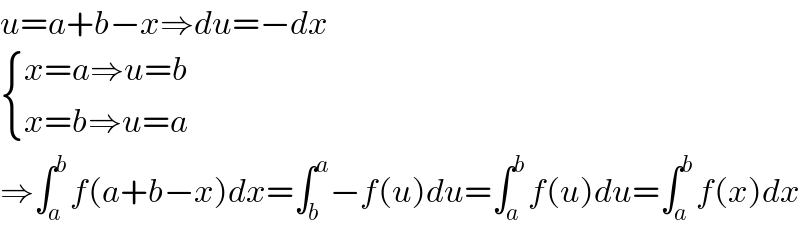
Answered by MJS last updated on 08/Oct/19
![∫_a ^b f(x)dx=[F(x)]_a ^b =F(b)−F(a) ∫_a ^b f(a+b−x)dx= [t=a+b−x ⇒ dx=−dt] =−∫_b ^a f(t)dt=−[F(t)]_b ^a =[F(t)]_a ^b =F(b)−F(a)](Q70822.png)
| ||
Question and Answers Forum | ||
Question Number 70818 by oyemi kemewari last updated on 08/Oct/19 | ||
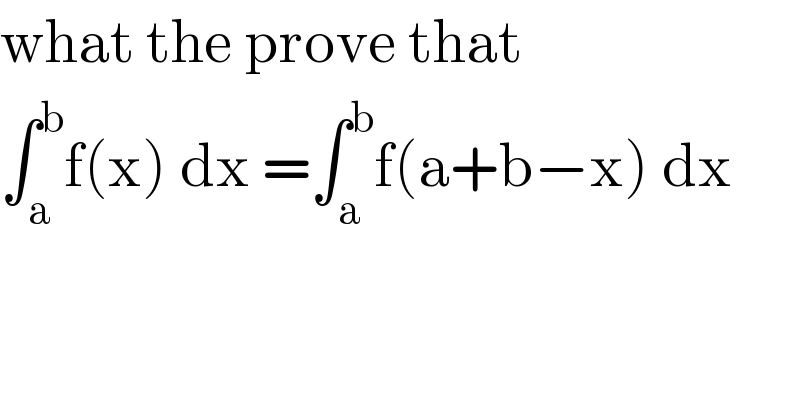 | ||
Commented by kaivan.ahmadi last updated on 08/Oct/19 | ||
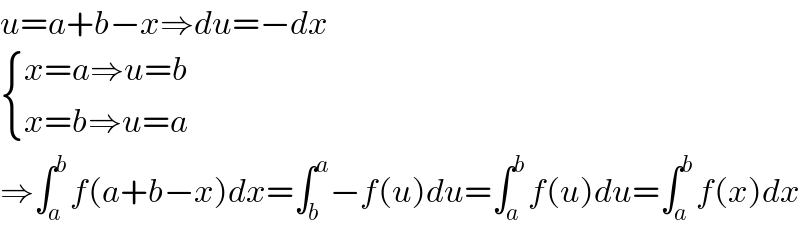 | ||
Answered by MJS last updated on 08/Oct/19 | ||
![∫_a ^b f(x)dx=[F(x)]_a ^b =F(b)−F(a) ∫_a ^b f(a+b−x)dx= [t=a+b−x ⇒ dx=−dt] =−∫_b ^a f(t)dt=−[F(t)]_b ^a =[F(t)]_a ^b =F(b)−F(a)](Q70822.png) | ||
| ||