Math Question and Answers


Question and Answers Forum

All Questions Topic List
Mechanics Questions
Previous in All Question Next in All Question
Previous in Mechanics Next in Mechanics
Question Number 70831 by ajfour last updated on 08/Oct/19

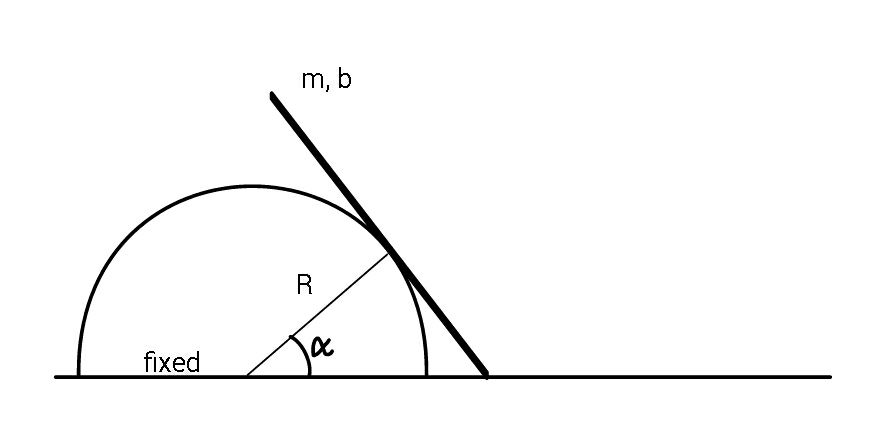
Commented by ajfour last updated on 08/Oct/19

$S t i c k o f m a s s m, l e n g t h b i s$ $r e l e a s e d a s s h o w n . A s i t s l i d e s$ $d o w n a n d b r e a k s c o n t a c t w i t h$ $h e m i s p h e r e, t h e t o p e n d i s a t$ $a n g u l a r p o s i t i o n β . A s s u m e$ $n o f r i c t i o n, f i n d β .$
	Answered by ajfour last updated on 08/Oct/19

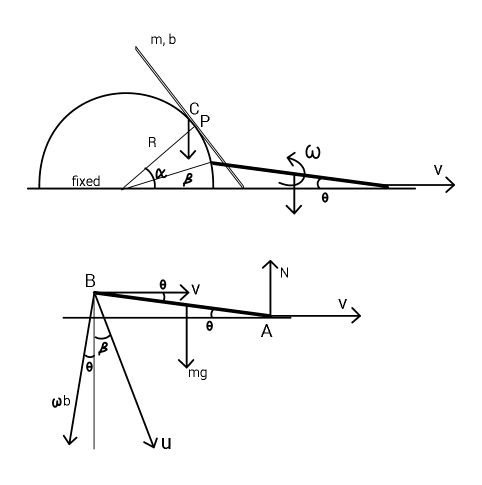
	Answered by mr W last updated on 08/Oct/19

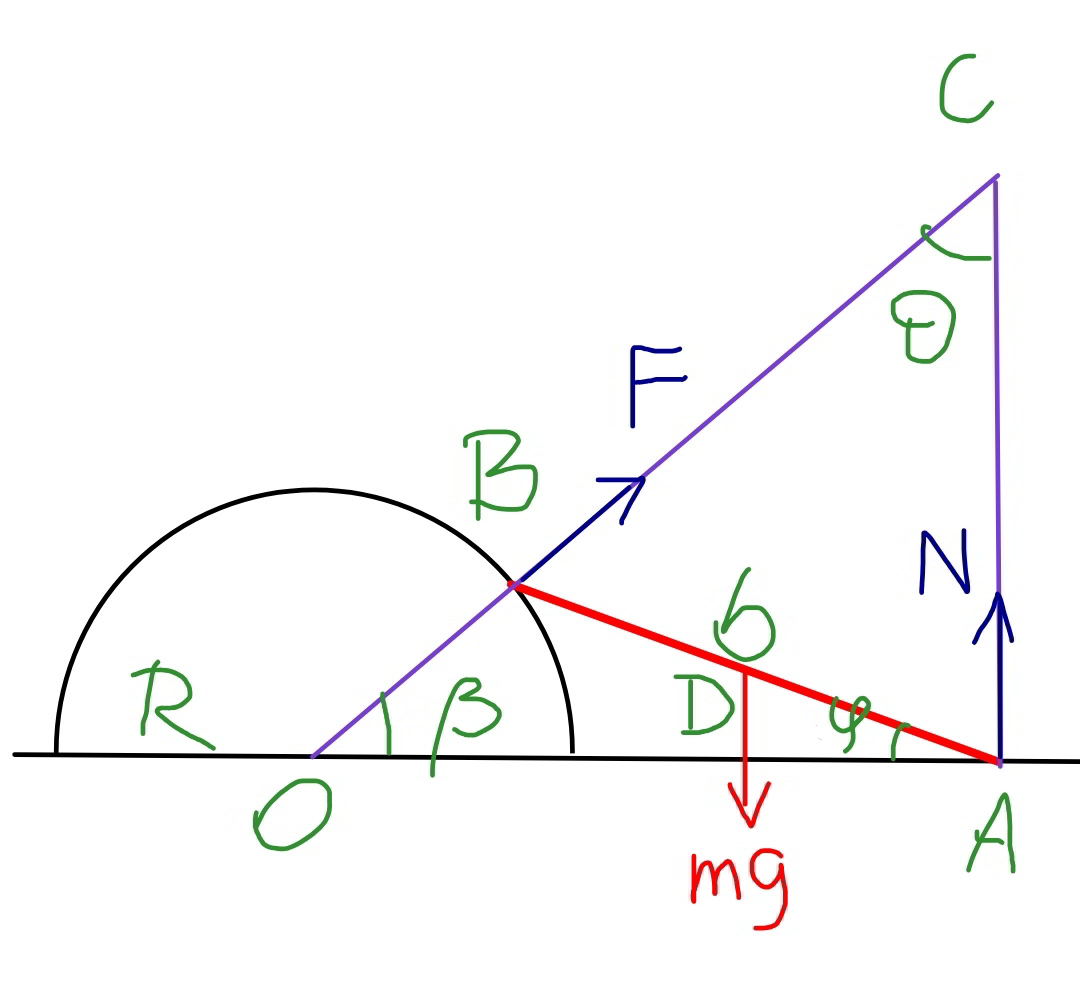
	Commented by ajfour last updated on 10/Oct/19

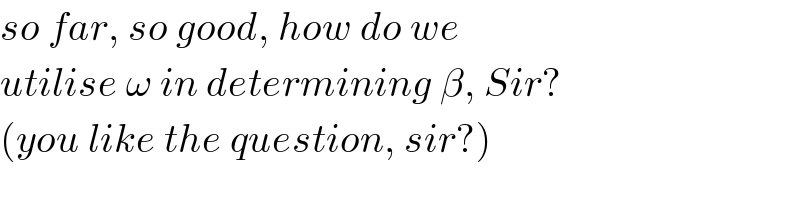
	$s o f a r, s o g o o d, h o w d o w e$ $u t i l i s e ω i n d e t e r m i n i n g β, S i r ?$ $(y o u l i k e t h e q u e s t i o n, s i r ?)$
	Commented by mr W last updated on 09/Oct/19
	$OA=R[cos β+(√((b^2 /R^2 )−sin^2 β))] AC=OA tan β=R[sin β+tan β(√((b^2 /R^2 )−sin^2 β))] BC=((OA)/(cos β))−R=(R/(cos β))(√((b^2 /R^2 )−sin^2 β)) CD^2 =((AC^2 +BC^2 )/2)−(b^2 /4) CD^2 =(R^2 /2){(1/(cos^2 β))((b^2 /R^2 )−sin^2 β)+sin^2 β[1+(1/(cos β))(√((b^2 /R^2 )−sin^2 β))]^2 }−(b^2 /4) I_C =I_0 +mCD^2 I_C =((mb^2 )/(12))+((mR^2 )/2){(1/(cos^2 β))((b^2 /R^2 )−sin^2 β)+sin^2 β[1+(1/(cos β))(√((b^2 /R^2 )−sin^2 β))]^2 }−((mb^2 )/4) I_C =((mR^2 )/2){(1/(cos^2 β))((b^2 /R^2 )−sin^2 β)+sin^2 β[1+(1/(cos β))(√((b^2 /R^2 )−sin^2 β))]^2 }−((mb^2 )/6) Δh=(R/2)((b/R) cos α−sin β) (1/2)I_C ω^2 =mgΔh ((R/2){(1/(cos^2 β))((b^2 /R^2 )−sin^2 β)+sin^2 β[1+(1/(cos β))(√((b^2 /R^2 )−sin^2 β))]^2 }−(b^2 /(6R^2 )))ω^2 =g((b/R) cos α−sin β) let λ=(b/R) ((1/2){(1/(cos^2 β))(λ^2 −sin^2 β)+sin^2 β[1+(1/(cos β))(√(λ^2 −sin^2 β))]^2 }−(λ^2 /6))ω^2 =(g/R)(λ cos α−sin β) ⇒ω=(√(g/R))(√((6(λ cos α−sin β))/(3{(1/(cos^2 β))(λ^2 −sin^2 β)+sin^2 β[1+(1/(cos β))(√(λ^2 −sin^2 β))]^2 }−λ^2 ))) ....$
	$O A = R [\cos β + \sqrt{\frac{b^{2}}{R^{2}} - \sin^{2} β}]$ $A C = O A \tan β = R [\sin β + \tan β \sqrt{\frac{b^{2}}{R^{2}} - \sin^{2} β}]$ $B C = \frac{O A}{\cos β} - R = \frac{R}{\cos β} \sqrt{\frac{b^{2}}{R^{2}} - \sin^{2} β}$ ${C D}^{2} = \frac{{A C}^{2} + {B C}^{2}}{2} - \frac{b^{2}}{4}$ ${C D}^{2} = \frac{R^{2}}{2} {\frac{1}{\cos^{2} β} (\frac{b^{2}}{R^{2}} - \sin^{2} β) + \sin^{2} β {[1 + \frac{1}{\cos β} \sqrt{\frac{b^{2}}{R^{2}} - \sin^{2} β}]}^{2}} - \frac{b^{2}}{4}$ $I_{C} = I_{0} + {m C D}^{2}$ $I_{C} = \frac{{m b}^{2}}{12} + \frac{{m R}^{2}}{2} {\frac{1}{\cos^{2} β} (\frac{b^{2}}{R^{2}} - \sin^{2} β) + \sin^{2} β {[1 + \frac{1}{\cos β} \sqrt{\frac{b^{2}}{R^{2}} - \sin^{2} β}]}^{2}} - \frac{{m b}^{2}}{4}$ $I_{C} = \frac{{m R}^{2}}{2} {\frac{1}{\cos^{2} β} (\frac{b^{2}}{R^{2}} - \sin^{2} β) + \sin^{2} β {[1 + \frac{1}{\cos β} \sqrt{\frac{b^{2}}{R^{2}} - \sin^{2} β}]}^{2}} - \frac{{m b}^{2}}{6}$ $Δ h = \frac{R}{2} (\frac{b}{R} \cos α - \sin β)$ $\frac{1}{2} I_{C} ω^{2} = m g Δ h$ $(\frac{R}{2} {\frac{1}{\cos^{2} β} (\frac{b^{2}}{R^{2}} - \sin^{2} β) + \sin^{2} β {[1 + \frac{1}{\cos β} \sqrt{\frac{b^{2}}{R^{2}} - \sin^{2} β}]}^{2}} - \frac{b^{2}}{6 R^{2}}) ω^{2} = g (\frac{b}{R} \cos α - \sin β)$ $l e t λ = \frac{b}{R}$ $(\frac{1}{2} {\frac{1}{\cos^{2} β} (λ^{2} - \sin^{2} β) + \sin^{2} β {[1 + \frac{1}{\cos β} \sqrt{λ^{2} - \sin^{2} β}]}^{2}} - \frac{λ^{2}}{6}) ω^{2} = \frac{g}{R} (λ \cos α - \sin β)$ $\Rightarrow ω = \sqrt{\frac{g}{R}} \sqrt{\frac{6 (λ \cos α - \sin β)}{3 {\frac{1}{\cos^{2} β} (λ^{2} - \sin^{2} β) + \sin^{2} β {[1 + \frac{1}{\cos β} \sqrt{λ^{2} - \sin^{2} β}]}^{2}} - λ^{2}}}$ $. . . .$
	Commented by mr W last updated on 10/Oct/19

	$n i c e q u e s t i o n s i r! b u t n o t e a s y .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum