Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 70886 by Omer Alattas last updated on 09/Oct/19

Commented by mathmax by abdo last updated on 10/Oct/19

1−cosu ∼(u^2 /2) and sinu ∼ u if u∈V(0) ⇒ 1−cos(((πt)/3))∼(((((πt)/3))^2 )/2) =π^2 (t^2 /(18)) and sin(((πt)/3))∼((πt)/3) ....

$$\mathrm{1}−{cosu}\:\sim\frac{{u}^{\mathrm{2}} }{\mathrm{2}}\:{and}\:{sinu}\:\sim\:{u}\:{if}\:{u}\in{V}\left(\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{1}−{cos}\left(\frac{\pi{t}}{\mathrm{3}}\right)\sim\frac{\left(\frac{\pi{t}}{\mathrm{3}}\right)^{\mathrm{2}} }{\mathrm{2}}\:=\pi^{\mathrm{2}} \frac{{t}^{\mathrm{2}} }{\mathrm{18}}\:{and}\:{sin}\left(\frac{\pi{t}}{\mathrm{3}}\right)\sim\frac{\pi{t}}{\mathrm{3}}\:.... \\ $$

Commented by mathmax by abdo last updated on 09/Oct/19

let f(x)=((1−4sin^2 (((πx)/6)))/(1−x^2 )) ⇒f(x)=((1−4((1−cos(((πx)/3)))/2))/(1−x^2 )) =((1−2(1−cos(((πx)/3))))/(1−x^2 )) =((2cos(((πx)/3))−1)/(1−x^2 )) =((1−2cos(((πx)/3)))/(x^2 −1)) changement x−1=t give f(x)=g(t)=((1−2cos((π/3)(1+t)))/(t(t+2))) =((1−2cos((π/3)+((πt)/3)))/(t(t+2))) =((1−2{(1/2)cos(((πt)/3))−((√3)/2)sin(((πt)/3))})/(t(t+2))) =((1−cos(((πt)/3))+(√3)sin(((πt)/3)))/(t(t+2))) x→1 ⇔t→0 so 1−co(((πt)/3))∼(((((πt)/3))^2 )/2) and sin(((πt)/3))∼((πt)/3) ⇒ g(t)∼ ((((π^2 t^2 )/(18)) +(√3)×((πt)/3))/(t(t+2))) ∼ ((((π^2 t)/(18))+((π(√3))/3))/(t+2)) →((π(√3))/6) ⇒ lim_(x→1) f(x)=((π(√3))/6)

$${let}\:{f}\left({x}\right)=\frac{\mathrm{1}−\mathrm{4}{sin}^{\mathrm{2}} \left(\frac{\pi{x}}{\mathrm{6}}\right)}{\mathrm{1}−{x}^{\mathrm{2}} }\:\Rightarrow{f}\left({x}\right)=\frac{\mathrm{1}−\mathrm{4}\frac{\mathrm{1}−{cos}\left(\frac{\pi{x}}{\mathrm{3}}\right)}{\mathrm{2}}}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}−\mathrm{2}\left(\mathrm{1}−{cos}\left(\frac{\pi{x}}{\mathrm{3}}\right)\right)}{\mathrm{1}−{x}^{\mathrm{2}} }\:=\frac{\mathrm{2}{cos}\left(\frac{\pi{x}}{\mathrm{3}}\right)−\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\:=\frac{\mathrm{1}−\mathrm{2}{cos}\left(\frac{\pi{x}}{\mathrm{3}}\right)}{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$${changement}\:{x}−\mathrm{1}={t}\:{give}\:{f}\left({x}\right)={g}\left({t}\right)=\frac{\mathrm{1}−\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{3}}\left(\mathrm{1}+{t}\right)\right)}{{t}\left({t}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}−\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{3}}+\frac{\pi{t}}{\mathrm{3}}\right)}{{t}\left({t}+\mathrm{2}\right)}\:=\frac{\mathrm{1}−\mathrm{2}\left\{\frac{\mathrm{1}}{\mathrm{2}}{cos}\left(\frac{\pi{t}}{\mathrm{3}}\right)−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sin}\left(\frac{\pi{t}}{\mathrm{3}}\right)\right\}}{{t}\left({t}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}−{cos}\left(\frac{\pi{t}}{\mathrm{3}}\right)+\sqrt{\mathrm{3}}{sin}\left(\frac{\pi{t}}{\mathrm{3}}\right)}{{t}\left({t}+\mathrm{2}\right)} \\ $$$${x}\rightarrow\mathrm{1}\:\Leftrightarrow{t}\rightarrow\mathrm{0}\:\:{so}\:\:\:\mathrm{1}−{co}\left(\frac{\pi{t}}{\mathrm{3}}\right)\sim\frac{\left(\frac{\pi{t}}{\mathrm{3}}\right)^{\mathrm{2}} }{\mathrm{2}}\:\:{and}\:{sin}\left(\frac{\pi{t}}{\mathrm{3}}\right)\sim\frac{\pi{t}}{\mathrm{3}}\:\Rightarrow \\ $$$${g}\left({t}\right)\sim\:\:\frac{\frac{\pi^{\mathrm{2}} {t}^{\mathrm{2}} }{\mathrm{18}}\:+\sqrt{\mathrm{3}}×\frac{\pi{t}}{\mathrm{3}}}{{t}\left({t}+\mathrm{2}\right)}\:\sim\:\:\frac{\frac{\pi^{\mathrm{2}} {t}}{\mathrm{18}}+\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{3}}}{{t}+\mathrm{2}}\:\rightarrow\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{6}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{1}} {f}\left({x}\right)=\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{6}} \\ $$

Commented by kaivan.ahmadi last updated on 09/Oct/19

Commented by Omer Alattas last updated on 09/Oct/19

thanks

$${thanks}\: \\ $$

Commented by Omer Alattas last updated on 09/Oct/19

I dont understsnd the last stap can you explan the last stap

$${I}\:{dont}\:{understsnd}\:{the}\:{last}\:{stap}\:{can}\:{you}\: \\ $$$${explan}\:{the}\:{last}\:{stap} \\ $$

Commented by Omer Alattas last updated on 10/Oct/19

I dont know what is this 1−cosu∼u^2 /2 can you till me how you get this?and whats mean this ∼

$${I}\:{dont}\:{know}\:{what}\:{is}\:{this}\:\:\mathrm{1}−{cosu}\sim{u}^{\mathrm{2}} /\mathrm{2}\:\:\:\: \\ $$$${can}\:{you}\:{till}\:{me}\:{how}\:{you}\:{get}\:{this}?{and}\:{whats}\:{mean}\:{this}\:\sim \\ $$

Commented by mathmax by abdo last updated on 10/Oct/19

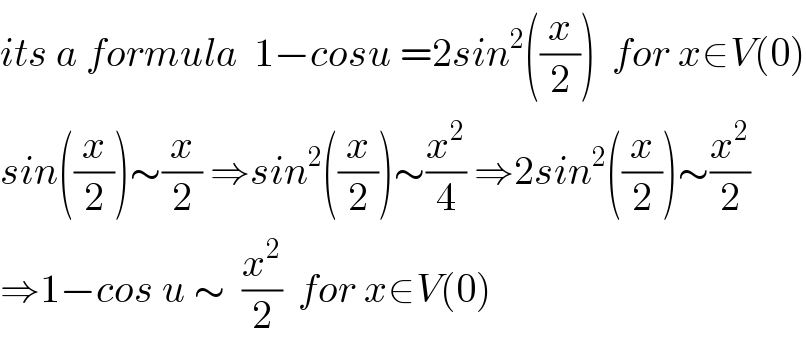
its a formula 1−cosu =2sin^2 ((x/2)) for x∈V(0) sin((x/2))∼(x/2) ⇒sin^2 ((x/2))∼(x^2 /4) ⇒2sin^2 ((x/2))∼(x^2 /2) ⇒1−cos u ∼ (x^2 /2) for x∈V(0)

$${its}\:{a}\:{formula}\:\:\mathrm{1}−{cosu}\:=\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\:\:{for}\:{x}\in{V}\left(\mathrm{0}\right) \\ $$$${sin}\left(\frac{{x}}{\mathrm{2}}\right)\sim\frac{{x}}{\mathrm{2}}\:\Rightarrow{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\sim\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\:\Rightarrow\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\sim\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\: \\ $$$$\Rightarrow\mathrm{1}−{cos}\:{u}\:\sim\:\:\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\:{for}\:{x}\in{V}\left(\mathrm{0}\right) \\ $$

Commented by mathmax by abdo last updated on 11/Oct/19

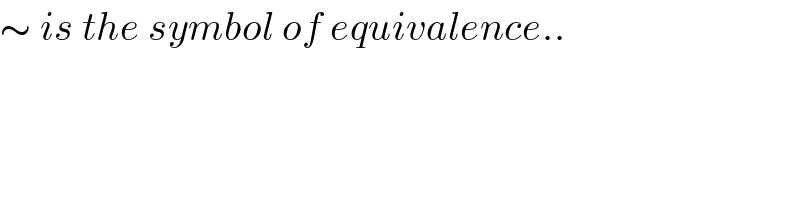
∼ is the symbol of equivalence..

$$\sim\:{is}\:{the}\:{symbol}\:{of}\:{equivalence}.. \\ $$

Commented by Omer Alattas last updated on 11/Oct/19

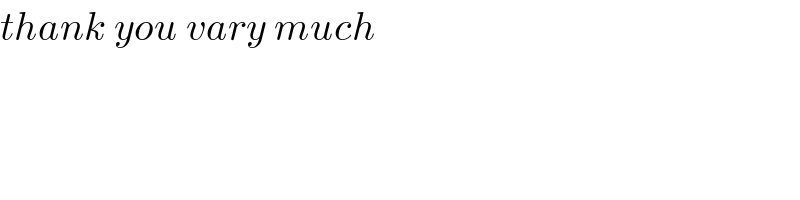
thank you vary much

$${thank}\:{you}\:{vary}\:{much}\: \\ $$$$ \\ $$

Commented by Omer Alattas last updated on 11/Oct/19

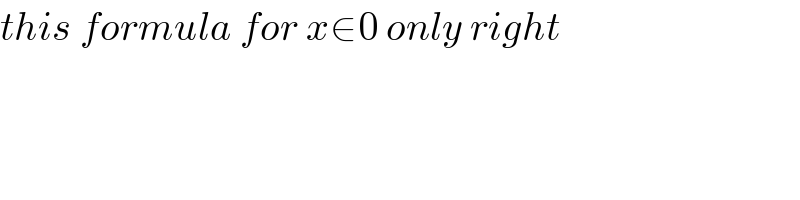
this formula for x∈0 only right

$${this}\:{formula}\:{for}\:{x}\in\mathrm{0}\:{only}\:{right}\: \\ $$

Commented by mathmax by abdo last updated on 11/Oct/19

yes.

$${yes}. \\ $$

Answered by Henri Boucatchou last updated on 09/Oct/19

lim_(x→1) ((1−4sin^2 ((𝛑/6)x))/(1−x^2 )) = lim_(x→1) (((4sin^2 ((𝛑/6)1)−4sin^2 ((𝛑/6)x))/(1−x))/((1−x^2 )/(1−x))) = ((4sin^2 ((𝛑/6)x)]′_((x=1)) )/(x^2 ]′_((x=1)) )) = ((4×2(𝛑/6)sin((𝛑/6)x)cos((𝛑/6)x)]_((x=1)) )/2) =((√3)/6)

$$\underset{\boldsymbol{{x}}\rightarrow\mathrm{1}} {\boldsymbol{{lim}}}\frac{\mathrm{1}−\mathrm{4}\boldsymbol{{sin}}^{\mathrm{2}} \left(\frac{\boldsymbol{\pi}}{\mathrm{6}}\boldsymbol{{x}}\right)}{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }\:=\:\underset{\boldsymbol{{x}}\rightarrow\mathrm{1}} {\boldsymbol{{lim}}}\frac{\frac{\mathrm{4}\boldsymbol{{sin}}^{\mathrm{2}} \left(\frac{\boldsymbol{\pi}}{\mathrm{6}}\mathrm{1}\right)−\mathrm{4}\boldsymbol{{sin}}^{\mathrm{2}} \left(\frac{\boldsymbol{\pi}}{\mathrm{6}}\boldsymbol{{x}}\right)}{\mathrm{1}−\boldsymbol{{x}}}}{\frac{\mathrm{1}−\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{1}−\boldsymbol{{x}}}}\:=\:\frac{\left.\mathrm{4}\boldsymbol{{sin}}^{\mathrm{2}} \left(\frac{\boldsymbol{\pi}}{\mathrm{6}}\boldsymbol{{x}}\right)\right]'_{\left(\boldsymbol{{x}}=\mathrm{1}\right)} }{\left.\boldsymbol{{x}}^{\mathrm{2}} \right]'_{\left(\boldsymbol{{x}}=\mathrm{1}\right)} }\:=\:\frac{\left.\mathrm{4}×\mathrm{2}\frac{\boldsymbol{\pi}}{\mathrm{6}}\boldsymbol{{sin}}\left(\frac{\boldsymbol{\pi}}{\mathrm{6}}\boldsymbol{{x}}\right)\boldsymbol{{cos}}\left(\frac{\boldsymbol{\pi}}{\mathrm{6}}\boldsymbol{{x}}\right)\right]_{\left(\boldsymbol{{x}}=\mathrm{1}\right)} }{\mathrm{2}} \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{6}} \\ $$

Answered by Henri Boucatchou last updated on 09/Oct/19

Sorry, the answer is (((√3) 𝛑)/6) insted of ((√3)/6)

$$\boldsymbol{{Sorry}},\:\boldsymbol{{the}}\:\:\boldsymbol{{answer}}\:\:\boldsymbol{{is}}\:\:\frac{\sqrt{\mathrm{3}}\:\boldsymbol{\pi}}{\mathrm{6}}\:\:\boldsymbol{{insted}}\:\:\boldsymbol{{of}}\:\:\frac{\sqrt{\mathrm{3}}}{\mathrm{6}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com