1+(z+2i)+(z+2i)^2 +(z+2i)^3 +(z+2i)^4 =0 find z , z∈C


Question and Answers Forum

All Questions Topic List
Others Questions
Previous in All Question Next in All Question
Previous in Others Next in Others
Question Number 70914 by 20190927 last updated on 09/Oct/19

$1 + (z + 2 i) + {(z + 2 i)}^{2} + {(z + 2 i)}^{3} + {(z + 2 i)}^{4} = 0$ $find z, z \in C$
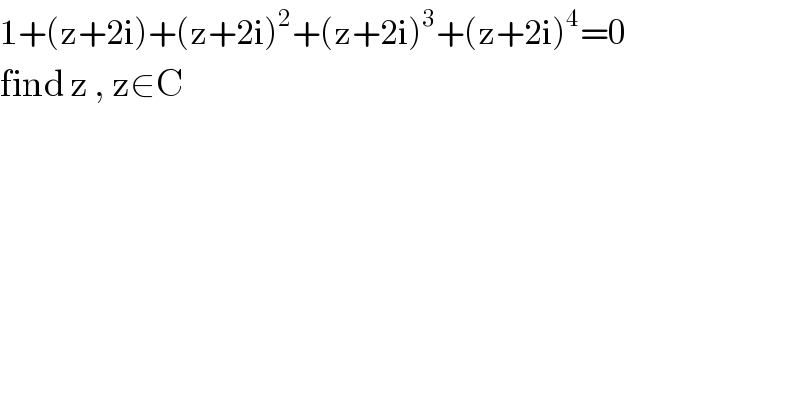
Commented by mathmax by abdo last updated on 09/Oct/19
$let x=z+2i (e) ⇔1+x+x^2 +x^3 +x^4 =0 ⇒((1−x^5 )/(1−x)) =0 and x≠1 ⇒ x^5 =1 and x≠1 butx^5 =1 ⇒x^5 =e^(i2kπ) ⇒x_k =e^((i2kπ)/5) and k∈[[1,4]] so the roots of (e) are z_k =x_k −2i z_k =e^((i2kπ)/5) −2i =cos(((2kπ)/5))+i(sin(((2kπ)/5))−2)=r_k e^(iθ_k ) with r_k =(√(cos(((2kπ)/5))^2 +(sin(((2kπ)/5))−2)^2 )) and θ_k =arctan{((sin(((2kπ)/5))−2)/(cos(((2kπ)/5))))} 1≤k≤4$
$l e t x = z + 2 i (e) \Leftrightarrow 1 + x + x^{2} + x^{3} + x^{4} = 0 \Rightarrow \frac{1 - x^{5}}{1 - x} = 0 a n d x \neq 1 \Rightarrow$ $x^{5} = 1 a n d x \neq 1 {b u t x}^{5} = 1 \Rightarrow x^{5} = e^{i 2 k π} \Rightarrow x_{k} = e^{\frac{i 2 k π}{5}}$ $a n d k \in [[1, 4]] s o t h e r o o t s o f (e) a r e z_{k} = x_{k} - 2 i$ $z_{k} = e^{\frac{i 2 k π}{5}} - 2 i = c o s (\frac{2 k π}{5}) + i (s i n (\frac{2 k π}{5}) - 2) = r_{k} e^{i θ_{k}}$ $w i t h r_{k} = \sqrt{c o s {(\frac{2 k π}{5})}^{2} + {(s i n (\frac{2 k π}{5}) - 2)}^{2}}$ $a n d θ_{k} = a r c t a n {\frac{s i n (\frac{2 k π}{5}) - 2}{c o s (\frac{2 k π}{5})}} 1 ⩽ k ⩽ 4$
Commented by 20190927 last updated on 10/Oct/19

$thank you$
Commented by mathmax by abdo last updated on 10/Oct/19

$y o u a r e w e l c o m e .$
	Answered by mind is power last updated on 09/Oct/19
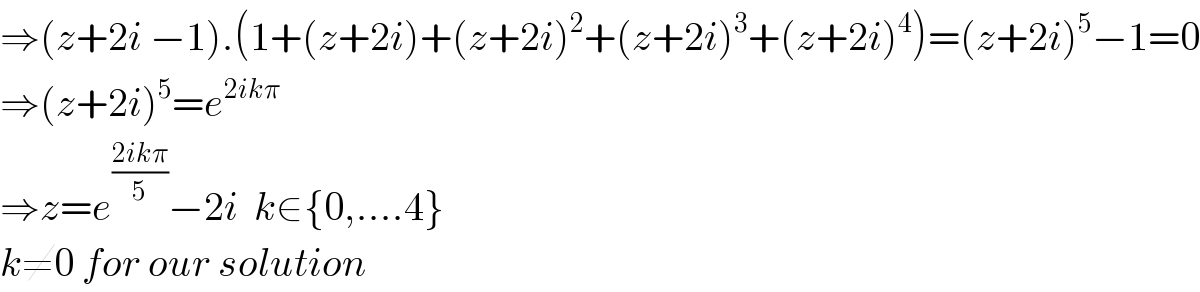
	$⇒(z+2i −1).(1+(z+2i)+(z+2i)^2 +(z+2i)^3 +(z+2i)^4 )=(z+2i)^5 −1=0 ⇒(z+2i)^5 =e^(2ikπ) ⇒z=e^((2ikπ)/5) −2i k∈{0,....4} k≠0 for our solution$
	$\Rightarrow (z + 2 i - 1) . (1 + (z + 2 i) + {(z + 2 i)}^{2} + {(z + 2 i)}^{3} + {(z + 2 i)}^{4}) = {(z + 2 i)}^{5} - 1 = 0$ $\Rightarrow {(z + 2 i)}^{5} = e^{2 i k π}$ $\Rightarrow z = e^{\frac{2 i k π}{5}} - 2 i k \in {0, . . . . 4}$ $k \neq 0 f o r o u r s o l u t i o n$
	Commented by 20190927 last updated on 10/Oct/19

	$thank you$
	Commented by mind is power last updated on 10/Oct/19

	$y^{'} r e w e l c o m$
	Answered by MJS last updated on 09/Oct/19

	$z = x - 2 i$ $x^{4} + x^{3} + x^{2} + x + 1 = 0$ $(x - 1) (x^{4} + x^{3} + x^{2} + x + 1) = 0$ $x^{5} - 1 = 0$ $\Rightarrow x_{0} = 1 not valid because we added it$ $x_{1} = - \frac{1}{4} + \frac{\sqrt{5}}{4} + \frac{\sqrt{10 + 2 \sqrt{5}}}{4} i$ $x_{2} = - \frac{1}{4} - \frac{\sqrt{5}}{4} + \frac{\sqrt{10 - 2 \sqrt{5}}}{4} i$ $x_{3} = - \frac{1}{4} - \frac{\sqrt{5}}{4} - \frac{\sqrt{10 - 2 \sqrt{5}}}{4} i$ $x_{4} = - \frac{1}{4} + \frac{\sqrt{5}}{4} - \frac{\sqrt{10 + 2 \sqrt{5}}}{4} i$ $z_{i} = x_{i} - 2 i$
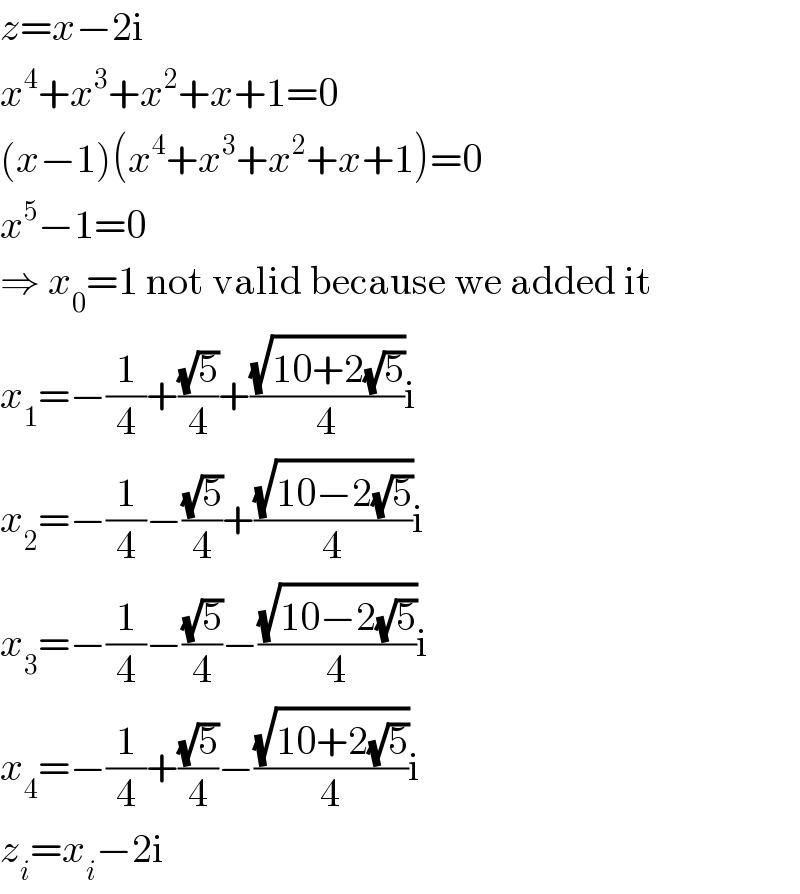
	Commented by 20190927 last updated on 10/Oct/19

	$thank you$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum