
Question Number 70949 by ajfour last updated on 10/Oct/19

Commented by ajfour last updated on 10/Oct/19
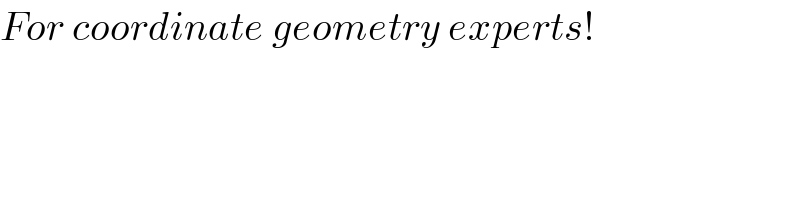
$${For}\:{coordinate}\:{geometry}\:{experts}! \\ $$
Commented by ajfour last updated on 10/Oct/19

$${Find}\:\boldsymbol{{k}}\:{in}\:{terms}\:{of}\:{a},{b},{c}. \\ $$
Commented by ajfour last updated on 10/Oct/19

$$\frac{\mathrm{1}}{\mathrm{4}{k}^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \theta}={b}+{b}\mathrm{sin}\:\theta \\ $$$$\frac{\mathrm{1}}{\mathrm{4}{k}^{\mathrm{2}} \mathrm{tan}\:^{\mathrm{2}} \phi}={a}+{a}\mathrm{sin}\:\phi \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{k}\mathrm{tan}\:\theta}+\frac{\mathrm{1}}{\mathrm{2}{k}\mathrm{tan}\:\phi}+{b}\mathrm{cos}\:\theta+{a}\mathrm{cos}\:\phi={c} \\ $$$${we}\:{need}\:{to}\:{eliminate}\:\theta\:{and}\:\phi \\ $$$${then}\:{determine}\:\boldsymbol{{k}}. \\ $$$$\left({please}\:{help}..\right) \\ $$
Answered by mr W last updated on 10/Oct/19
![B(p,kp^2 ) center of circle S(q,r) tan θ=y′=2kp=((q−p)/(kp^2 −r)) ⇒q−p=2kp(kp^2 −r) (p−q)^2 +(kp^2 −r)^2 =r^2 (4k^2 p^2 +1)(kp^2 −r)^2 =r^2 let P=p^2 (4k^2 P+1)(kP−r)^2 =r^2 ⇒4k^3 P^2 −k(8kr−1)P+2r(2kr−1)=0 ⇒P=p^2 =((8kr−1+(√(16kr+1)))/(8k^2 )) ⇒p=(1/(2k))(√((8kr−1+(√(16kr+1)))/2)) q=[2k(kp^2 −r)+1]p ⇒q=((3+(√(16kr+1)))/(8k))(√((8kr−1+(√(16kr+1)))/2)) ⇒q_a =((3+(√(16ka+1)))/(8k))(√((8ka−1+(√(16ka+1)))/2)) ⇒q_b =((3+(√(16kb+1)))/(8k))(√((8kb−1+(√(16kb+1)))/2)) q_a +q_b =c ⇒((3+(√(16ka+1)))/(8k))(√((8ka−1+(√(16ka+1)))/2)) +((3+(√(16ka+1)))/(8k))(√((8ka−1+(√(16ka+1)))/2))=c ⇒k=.....in terms of a,b,c examples: a=3, b=2, c=8 ⇒k=1.2412 a=4, b=4, c=10 ⇒k=4.2324](Q71007.png)
$${B}\left({p},{kp}^{\mathrm{2}} \right) \\ $$$${center}\:{of}\:{circle}\:{S}\left({q},{r}\right) \\ $$$$\mathrm{tan}\:\theta={y}'=\mathrm{2}{kp}=\frac{{q}−{p}}{{kp}^{\mathrm{2}} −{r}} \\ $$$$\Rightarrow{q}−{p}=\mathrm{2}{kp}\left({kp}^{\mathrm{2}} −{r}\right) \\ $$$$\left({p}−{q}\right)^{\mathrm{2}} +\left({kp}^{\mathrm{2}} −{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\left(\mathrm{4}{k}^{\mathrm{2}} {p}^{\mathrm{2}} +\mathrm{1}\right)\left({kp}^{\mathrm{2}} −{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${let}\:{P}={p}^{\mathrm{2}} \\ $$$$\left(\mathrm{4}{k}^{\mathrm{2}} {P}+\mathrm{1}\right)\left({kP}−{r}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{4}{k}^{\mathrm{3}} {P}^{\mathrm{2}} −{k}\left(\mathrm{8}{kr}−\mathrm{1}\right){P}+\mathrm{2}{r}\left(\mathrm{2}{kr}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{P}={p}^{\mathrm{2}} =\frac{\mathrm{8}{kr}−\mathrm{1}+\sqrt{\mathrm{16}{kr}+\mathrm{1}}}{\mathrm{8}{k}^{\mathrm{2}} } \\ $$$$\Rightarrow{p}=\frac{\mathrm{1}}{\mathrm{2}{k}}\sqrt{\frac{\mathrm{8}{kr}−\mathrm{1}+\sqrt{\mathrm{16}{kr}+\mathrm{1}}}{\mathrm{2}}} \\ $$$${q}=\left[\mathrm{2}{k}\left({kp}^{\mathrm{2}} −{r}\right)+\mathrm{1}\right]{p} \\ $$$$\Rightarrow{q}=\frac{\mathrm{3}+\sqrt{\mathrm{16}{kr}+\mathrm{1}}}{\mathrm{8}{k}}\sqrt{\frac{\mathrm{8}{kr}−\mathrm{1}+\sqrt{\mathrm{16}{kr}+\mathrm{1}}}{\mathrm{2}}} \\ $$$$\Rightarrow{q}_{{a}} =\frac{\mathrm{3}+\sqrt{\mathrm{16}{ka}+\mathrm{1}}}{\mathrm{8}{k}}\sqrt{\frac{\mathrm{8}{ka}−\mathrm{1}+\sqrt{\mathrm{16}{ka}+\mathrm{1}}}{\mathrm{2}}} \\ $$$$\Rightarrow{q}_{{b}} =\frac{\mathrm{3}+\sqrt{\mathrm{16}{kb}+\mathrm{1}}}{\mathrm{8}{k}}\sqrt{\frac{\mathrm{8}{kb}−\mathrm{1}+\sqrt{\mathrm{16}{kb}+\mathrm{1}}}{\mathrm{2}}} \\ $$$${q}_{{a}} +{q}_{{b}} ={c} \\ $$$$\Rightarrow\frac{\mathrm{3}+\sqrt{\mathrm{16}{ka}+\mathrm{1}}}{\mathrm{8}{k}}\sqrt{\frac{\mathrm{8}{ka}−\mathrm{1}+\sqrt{\mathrm{16}{ka}+\mathrm{1}}}{\mathrm{2}}} \\ $$$$\:\:+\frac{\mathrm{3}+\sqrt{\mathrm{16}{ka}+\mathrm{1}}}{\mathrm{8}{k}}\sqrt{\frac{\mathrm{8}{ka}−\mathrm{1}+\sqrt{\mathrm{16}{ka}+\mathrm{1}}}{\mathrm{2}}}={c} \\ $$$$\Rightarrow{k}=.....{in}\:{terms}\:{of}\:{a},{b},{c} \\ $$$$ \\ $$$${examples}: \\ $$$${a}=\mathrm{3},\:{b}=\mathrm{2},\:{c}=\mathrm{8} \\ $$$$\Rightarrow{k}=\mathrm{1}.\mathrm{2412} \\ $$$${a}=\mathrm{4},\:{b}=\mathrm{4},\:{c}=\mathrm{10} \\ $$$$\Rightarrow{k}=\mathrm{4}.\mathrm{2324} \\ $$
Commented by mr W last updated on 10/Oct/19

Commented by mr W last updated on 10/Oct/19

Commented by ajfour last updated on 10/Oct/19

$${Thank}\:{you}\:{Sir},\:{you}\:{brought}\:{it} \\ $$$${to}\:{a}\:{single}\:{equation}\:{in}\:{k}. \\ $$$${Very}\:{nice}\:{solution}! \\ $$
