Question Number 71073 by TawaTawa last updated on 11/Oct/19

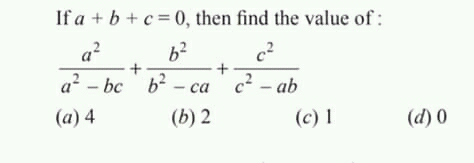
Commented byPrithwish sen last updated on 11/Oct/19

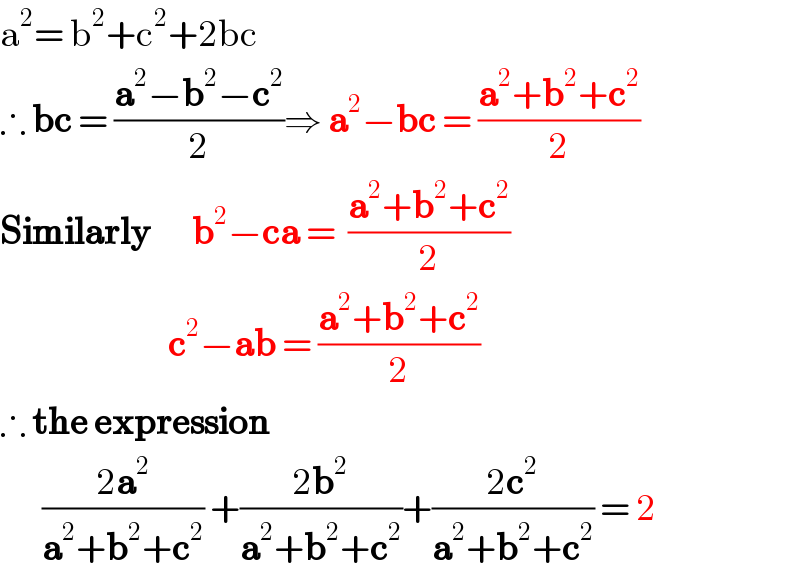
a^2 = b^2 +c^2 +2bc ∴ bc = ((a^2 −b^2 −c^2 )/2)⇒ a^2 −bc = ((a^2 +b^2 +c^2 )/2) Similarly b^2 −ca = ((a^2 +b^2 +c^2 )/2) c^2 −ab = ((a^2 +b^2 +c^2 )/2) ∴ the expression ((2a^2 )/(a^2 +b^2 +c^2 )) +((2b^2 )/(a^2 +b^2 +c^2 ))+((2c^2 )/(a^2 +b^2 +c^2 )) = 2

Commented byHenri Boucatchou last updated on 11/Oct/19

Nice...

Commented byPrithwish sen last updated on 11/Oct/19

Thank you Sir.

Commented byTawaTawa last updated on 11/Oct/19

God bless you sir

Answered by $@ty@m123 last updated on 11/Oct/19

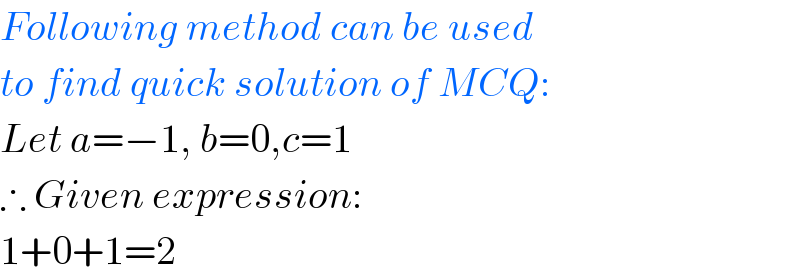
Following method can be used to find quick solution of MCQ: Let a=−1, b=0,c=1 ∴ Given expression: 1+0+1=2

Commented byMJS last updated on 11/Oct/19

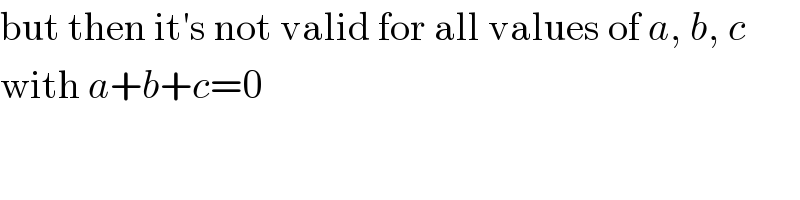
but then it′s not valid for all values of a, b, c with a+b+c=0

Commented by$@ty@m123 last updated on 11/Oct/19

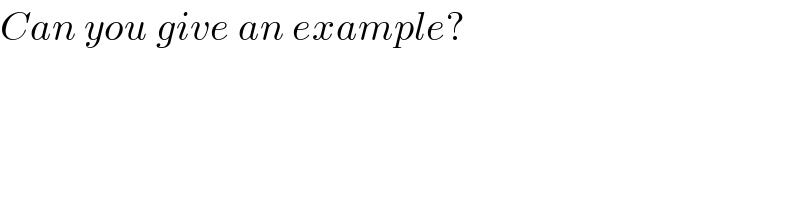
Can you give an example?

Commented by$@ty@m123 last updated on 11/Oct/19

Of course, this is not a proper (traditional) way, but in MCQ type tests, we need tricky approach to save time.

Answered by MJS last updated on 11/Oct/19

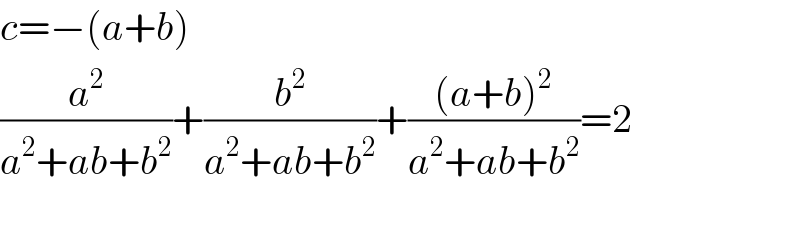
c=−(a+b) (a^2 /(a^2 +ab+b^2 ))+(b^2 /(a^2 +ab+b^2 ))+(((a+b)^2 )/(a^2 +ab+b^2 ))=2

Commented byPrithwish sen last updated on 11/Oct/19

<Excellent Sir !

Commented byMJS last updated on 11/Oct/19

thank you

Commented byTawaTawa last updated on 11/Oct/19

God bless you sir

Answered by peter frank last updated on 11/Oct/19

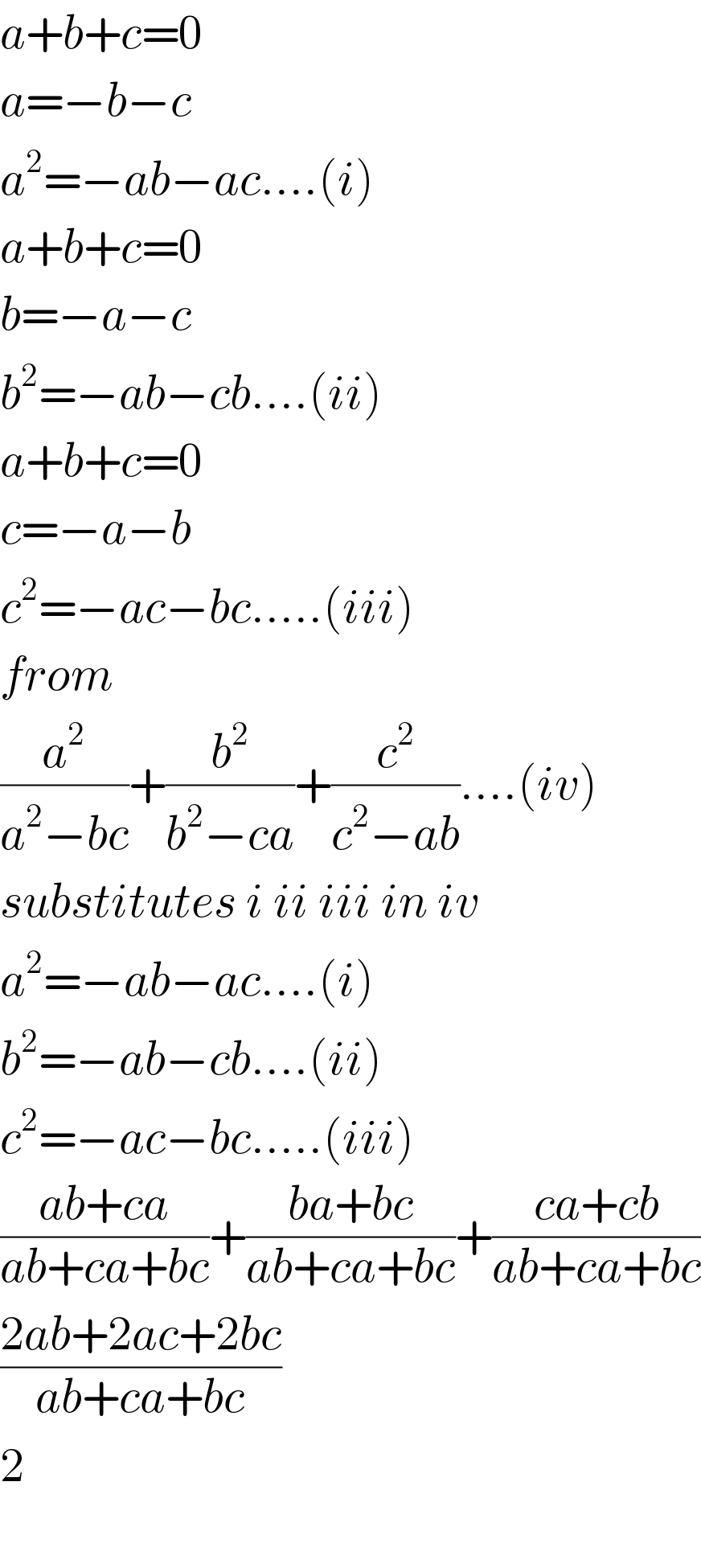
a+b+c=0 a=−b−c a^2 =−ab−ac....(i) a+b+c=0 b=−a−c b^2 =−ab−cb....(ii) a+b+c=0 c=−a−b c^2 =−ac−bc.....(iii) from (a^2 /(a^2 −bc))+(b^2 /(b^2 −ca))+(c^2 /(c^2 −ab))....(iv) substitutes i ii iii in iv a^2 =−ab−ac....(i) b^2 =−ab−cb....(ii) c^2 =−ac−bc.....(iii) ((ab+ca)/(ab+ca+bc))+((ba+bc)/(ab+ca+bc))+((ca+cb)/(ab+ca+bc)) ((2ab+2ac+2bc)/(ab+ca+bc)) 2

Commented byTawaTawa last updated on 11/Oct/19

God bless you sir