
Question Number 7127 by Tawakalitu. last updated on 11/Aug/16
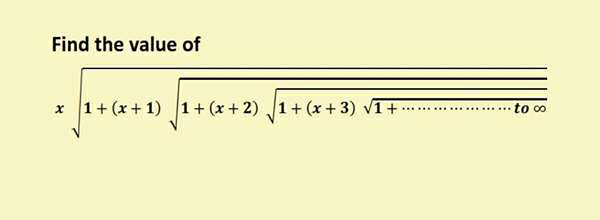
Commented by Yozzii last updated on 11/Aug/16
![Let u=x(√(1+(x+1)+(√(1+(x+2)+(√(1+(x+3)+(√(1+....)))))))) ⇒(u/x)=(√(1+(x+1)+(√(1+(x+2)+(√(1+(x+3)+(√(1+....)))))))) let n=x+1⇒x=n−1. ∴(u/(n−1))=(√(1+n+(√(1+(n+1)+(√(1+(n+2)+(√(1+(n+3)+(√(1+.....)))))))))) (u^2 /((n−1)^2 ))−n−1=(√(1+(n+1)+(√(1+(n+2)+(√(1+(n+3)+(√(1+....)))))))) But for any x≠0, (u/x) has the form (√(1+(x+1)+(√(1+(x+2)+(√(1+(x+3)+(√(1+....)))))))) Therefore, if (√(1+(x+1)+(√(1+(x+2)+(√(1+(x+3)+(√(1+....)))))))) converges to (u/x) ⇒(√(1+(n+1)+(√(1+(n+2)+(√(1+(n+3)+(√(1+.....)))))))) converges to (u/n). (u^2 /((n−1)^2 ))−n−1=(u/n) nu^2 −n(n+1)(n−1)^2 =u(n−1)^2 nu^2 −(n−1)^2 u−n(n+1)(n−1)^2 =0 ∴ u=(((n−1)^2 ±(√((n−1)^4 +4×n×n(n+1)(n−1)^2 )))/(2n)) u=(((n−1)^2 ±(n−1)^2 (√((n−1)^2 +4n^2 (n+1))))/(2n)) n=x+1 ∴u=x[((1±(√(x^2 +4(x+1)^2 (x+2))))/(2(x+1)))] u=x[((1±(√(x^2 +4(x^2 +2x+1)(x+2))))/(2(x+1)))] u=x[((1±(√(x^2 +4(x^3 +2x^2 +2x^2 +4x+x+2))))/(2(x+1)))] u=x[((1±(√(4x^3 +17x^2 +20x+8)))/(2(x+1)))] Let r(x)=4x^3 +17x^2 +20x+8 ∴ if r′(x)=0⇒12x^2 + 34x+20=0 6x^2 +17x+10=0 ∴x=((−17±(√(289−4×6×10)))/(12))=((−17±7)/(12)) x=((−24)/(12)),((−10)/(12)) or x=−2,((−5)/6) r(−2)=4×(−8)+17×4−20×2+8 r(−2)=−32+68−40+8=4>1>0 If r(x)≥1⇒4x^3 +17x^2 +20x+7≥0 4x^2 (x+1)+20x(x+1)−7(x^2 −1)≥0 (x+1)(4x^2 +20x−7(x−1))≥0 (x+1)(4x^2 +13x+7)≥0 x=((−13±(√(169−4×4×7)))/8) x=((−13±(√(57)))/8) (x+1)(x+((13+(√(57)))/8))(x+((13−(√(57)))/8))≥0 −−−−−−−−(−1)++++++++++ −−−−r_1 +++++++++++++++ −−−−−−−−−−−−−−r_2 +++++ r_1 ≤x≤−1, x≥r_2 If x=r_1 or r_2 (not −1), u=x[((1±1)/(2(x+1)))]=0 or (x/(x+1)) But, u=0 iff x=0 and x≠0 ∴ u=(x/(x+1)) if x= r_(1 ) or r_2 . If r_1 <x<−1 or x>r_2 , 1−(√(4x^3 +17x^2 +20x+8))<1−1=0 But, (√(1+(x+1)+(√(1+(x+2)+(√(1+(x+3)+(√(1+...))))))))>0 ∴ u=((x(1−(√(4x^3 +17x^2 +20x+8))))/(2(x+1))) for ((−13−(√(57)))/8)=r_1 <x<−1 and u=((x(1+(√(4x^3 +17x^2 +20x+8))))/(2(x+1))) for x>r_2 =((−13+(√(57)))/8)](Q7129.png)
$${Let}\:{u}={x}\sqrt{\mathrm{1}+\left({x}+\mathrm{1}\right)+\sqrt{\mathrm{1}+\left({x}+\mathrm{2}\right)+\sqrt{\mathrm{1}+\left({x}+\mathrm{3}\right)+\sqrt{\mathrm{1}+....}}}} \\ $$$$\Rightarrow\frac{{u}}{{x}}=\sqrt{\mathrm{1}+\left({x}+\mathrm{1}\right)+\sqrt{\mathrm{1}+\left({x}+\mathrm{2}\right)+\sqrt{\mathrm{1}+\left({x}+\mathrm{3}\right)+\sqrt{\mathrm{1}+....}}}} \\ $$$${let}\:{n}={x}+\mathrm{1}\Rightarrow{x}={n}−\mathrm{1}. \\ $$$$\therefore\frac{{u}}{{n}−\mathrm{1}}=\sqrt{\mathrm{1}+{n}+\sqrt{\mathrm{1}+\left({n}+\mathrm{1}\right)+\sqrt{\mathrm{1}+\left({n}+\mathrm{2}\right)+\sqrt{\mathrm{1}+\left({n}+\mathrm{3}\right)+\sqrt{\mathrm{1}+.....}}}}} \\ $$$$\frac{{u}^{\mathrm{2}} }{\left({n}−\mathrm{1}\right)^{\mathrm{2}} }−{n}−\mathrm{1}=\sqrt{\mathrm{1}+\left({n}+\mathrm{1}\right)+\sqrt{\mathrm{1}+\left({n}+\mathrm{2}\right)+\sqrt{\mathrm{1}+\left({n}+\mathrm{3}\right)+\sqrt{\mathrm{1}+....}}}} \\ $$$${But}\:{for}\:{any}\:{x}\neq\mathrm{0},\:\frac{{u}}{{x}}\:{has}\:{the}\:{form}\:\sqrt{\mathrm{1}+\left({x}+\mathrm{1}\right)+\sqrt{\mathrm{1}+\left({x}+\mathrm{2}\right)+\sqrt{\mathrm{1}+\left({x}+\mathrm{3}\right)+\sqrt{\mathrm{1}+....}}}} \\ $$$${Therefore},\:{if}\:\sqrt{\mathrm{1}+\left({x}+\mathrm{1}\right)+\sqrt{\mathrm{1}+\left({x}+\mathrm{2}\right)+\sqrt{\mathrm{1}+\left({x}+\mathrm{3}\right)+\sqrt{\mathrm{1}+....}}}}\:{converges}\:{to}\:\frac{{u}}{{x}} \\ $$$$\Rightarrow\sqrt{\mathrm{1}+\left({n}+\mathrm{1}\right)+\sqrt{\mathrm{1}+\left({n}+\mathrm{2}\right)+\sqrt{\mathrm{1}+\left({n}+\mathrm{3}\right)+\sqrt{\mathrm{1}+.....}}}}\:{converges}\:{to}\:\frac{{u}}{{n}}. \\ $$$$\frac{{u}^{\mathrm{2}} }{\left({n}−\mathrm{1}\right)^{\mathrm{2}} }−{n}−\mathrm{1}=\frac{{u}}{{n}} \\ $$$${nu}^{\mathrm{2}} −{n}\left({n}+\mathrm{1}\right)\left({n}−\mathrm{1}\right)^{\mathrm{2}} ={u}\left({n}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$${nu}^{\mathrm{2}} −\left({n}−\mathrm{1}\right)^{\mathrm{2}} {u}−{n}\left({n}+\mathrm{1}\right)\left({n}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\therefore\:{u}=\frac{\left({n}−\mathrm{1}\right)^{\mathrm{2}} \pm\sqrt{\left({n}−\mathrm{1}\right)^{\mathrm{4}} +\mathrm{4}×{n}×{n}\left({n}+\mathrm{1}\right)\left({n}−\mathrm{1}\right)^{\mathrm{2}} }}{\mathrm{2}{n}} \\ $$$${u}=\frac{\left({n}−\mathrm{1}\right)^{\mathrm{2}} \pm\left({n}−\mathrm{1}\right)^{\mathrm{2}} \sqrt{\left({n}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)}}{\mathrm{2}{n}} \\ $$$${n}={x}+\mathrm{1} \\ $$$$\therefore{u}={x}\left[\frac{\mathrm{1}\pm\sqrt{{x}^{\mathrm{2}} +\mathrm{4}\left({x}+\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{2}\right)}}{\mathrm{2}\left({x}+\mathrm{1}\right)}\right] \\ $$$${u}={x}\left[\frac{\mathrm{1}\pm\sqrt{{x}^{\mathrm{2}} +\mathrm{4}\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)}}{\mathrm{2}\left({x}+\mathrm{1}\right)}\right] \\ $$$${u}={x}\left[\frac{\mathrm{1}\pm\sqrt{{x}^{\mathrm{2}} +\mathrm{4}\left({x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}+{x}+\mathrm{2}\right)}}{\mathrm{2}\left({x}+\mathrm{1}\right)}\right] \\ $$$${u}={x}\left[\frac{\mathrm{1}\pm\sqrt{\mathrm{4}{x}^{\mathrm{3}} +\mathrm{17}{x}^{\mathrm{2}} +\mathrm{20}{x}+\mathrm{8}}}{\mathrm{2}\left({x}+\mathrm{1}\right)}\right] \\ $$$$ \\ $$$${Let}\:{r}\left({x}\right)=\mathrm{4}{x}^{\mathrm{3}} +\mathrm{17}{x}^{\mathrm{2}} +\mathrm{20}{x}+\mathrm{8} \\ $$$$\therefore\:{if}\:{r}'\left({x}\right)=\mathrm{0}\Rightarrow\mathrm{12}{x}^{\mathrm{2}} +\:\mathrm{34}{x}+\mathrm{20}=\mathrm{0} \\ $$$$\mathrm{6}{x}^{\mathrm{2}} +\mathrm{17}{x}+\mathrm{10}=\mathrm{0} \\ $$$$\therefore{x}=\frac{−\mathrm{17}\pm\sqrt{\mathrm{289}−\mathrm{4}×\mathrm{6}×\mathrm{10}}}{\mathrm{12}}=\frac{−\mathrm{17}\pm\mathrm{7}}{\mathrm{12}} \\ $$$${x}=\frac{−\mathrm{24}}{\mathrm{12}},\frac{−\mathrm{10}}{\mathrm{12}}\:{or}\:{x}=−\mathrm{2},\frac{−\mathrm{5}}{\mathrm{6}} \\ $$$${r}\left(−\mathrm{2}\right)=\mathrm{4}×\left(−\mathrm{8}\right)+\mathrm{17}×\mathrm{4}−\mathrm{20}×\mathrm{2}+\mathrm{8} \\ $$$${r}\left(−\mathrm{2}\right)=−\mathrm{32}+\mathrm{68}−\mathrm{40}+\mathrm{8}=\mathrm{4}>\mathrm{1}>\mathrm{0} \\ $$$${If}\:{r}\left({x}\right)\geqslant\mathrm{1}\Rightarrow\mathrm{4}{x}^{\mathrm{3}} +\mathrm{17}{x}^{\mathrm{2}} +\mathrm{20}{x}+\mathrm{7}\geqslant\mathrm{0} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)+\mathrm{20}{x}\left({x}+\mathrm{1}\right)−\mathrm{7}\left({x}^{\mathrm{2}} −\mathrm{1}\right)\geqslant\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{20}{x}−\mathrm{7}\left({x}−\mathrm{1}\right)\right)\geqslant\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{13}{x}+\mathrm{7}\right)\geqslant\mathrm{0} \\ $$$${x}=\frac{−\mathrm{13}\pm\sqrt{\mathrm{169}−\mathrm{4}×\mathrm{4}×\mathrm{7}}}{\mathrm{8}} \\ $$$${x}=\frac{−\mathrm{13}\pm\sqrt{\mathrm{57}}}{\mathrm{8}} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}+\frac{\mathrm{13}+\sqrt{\mathrm{57}}}{\mathrm{8}}\right)\left({x}+\frac{\mathrm{13}−\sqrt{\mathrm{57}}}{\mathrm{8}}\right)\geqslant\mathrm{0} \\ $$$$−−−−−−−−\left(−\mathrm{1}\right)++++++++++ \\ $$$$−−−−{r}_{\mathrm{1}} +++++++++++++++ \\ $$$$−−−−−−−−−−−−−−{r}_{\mathrm{2}} +++++ \\ $$$${r}_{\mathrm{1}} \leqslant{x}\leqslant−\mathrm{1},\:{x}\geqslant{r}_{\mathrm{2}} \\ $$$${If}\:{x}={r}_{\mathrm{1}} \:{or}\:{r}_{\mathrm{2}} \:\left({not}\:−\mathrm{1}\right),\:{u}={x}\left[\frac{\mathrm{1}\pm\mathrm{1}}{\mathrm{2}\left({x}+\mathrm{1}\right)}\right]=\mathrm{0}\:{or}\:\frac{{x}}{{x}+\mathrm{1}} \\ $$$${But},\:{u}=\mathrm{0}\:{iff}\:{x}=\mathrm{0}\:{and}\:{x}\neq\mathrm{0}\:\therefore\:{u}=\frac{{x}}{{x}+\mathrm{1}} \\ $$$${if}\:{x}=\:{r}_{\mathrm{1}\:} {or}\:{r}_{\mathrm{2}} . \\ $$$${If}\:{r}_{\mathrm{1}} <{x}<−\mathrm{1}\:{or}\:{x}>{r}_{\mathrm{2}} ,\:\mathrm{1}−\sqrt{\mathrm{4}{x}^{\mathrm{3}} +\mathrm{17}{x}^{\mathrm{2}} +\mathrm{20}{x}+\mathrm{8}}<\mathrm{1}−\mathrm{1}=\mathrm{0} \\ $$$${But},\:\sqrt{\mathrm{1}+\left({x}+\mathrm{1}\right)+\sqrt{\mathrm{1}+\left({x}+\mathrm{2}\right)+\sqrt{\mathrm{1}+\left({x}+\mathrm{3}\right)+\sqrt{\mathrm{1}+...}}}}>\mathrm{0} \\ $$$$\therefore\:{u}=\frac{{x}\left(\mathrm{1}−\sqrt{\mathrm{4}{x}^{\mathrm{3}} +\mathrm{17}{x}^{\mathrm{2}} +\mathrm{20}{x}+\mathrm{8}}\right)}{\mathrm{2}\left({x}+\mathrm{1}\right)}\:{for}\:\frac{−\mathrm{13}−\sqrt{\mathrm{57}}}{\mathrm{8}}={r}_{\mathrm{1}} <{x}<−\mathrm{1} \\ $$$${and}\:{u}=\frac{{x}\left(\mathrm{1}+\sqrt{\mathrm{4}{x}^{\mathrm{3}} +\mathrm{17}{x}^{\mathrm{2}} +\mathrm{20}{x}+\mathrm{8}}\right)}{\mathrm{2}\left({x}+\mathrm{1}\right)}\:{for}\:{x}>{r}_{\mathrm{2}} =\frac{−\mathrm{13}+\sqrt{\mathrm{57}}}{\mathrm{8}} \\ $$
Commented by Tawakalitu. last updated on 11/Aug/16
$${Great}\:{job}\:.....\:{Thank}\:{you}\:{very}\:{much}\:{sir}.\:{i}\:{appreciate}\:{your}\:{effort} \\ $$
