Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 71326 by sadimuhmud 136 last updated on 13/Oct/19

$${(-64)}^{\frac{1}{6}}=?\left(\mathbf{I}\mathrm{s}\mathrm{there}\mathrm{any}\mathrm{short}\mathrm{cut}\mathrm{for}\mathrm{mcq}\right)$$

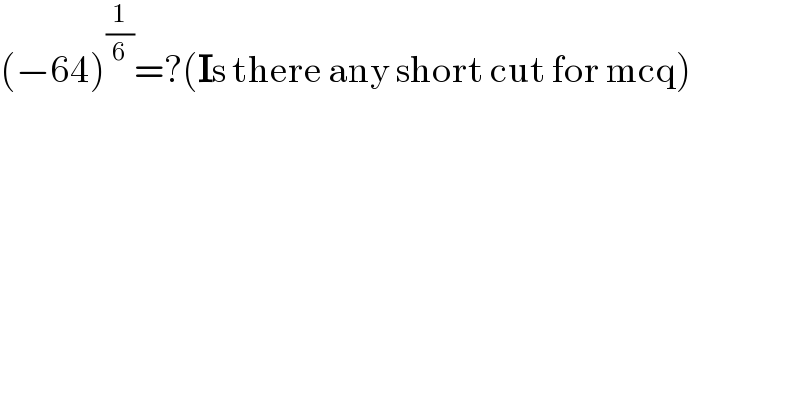
Answered by MJS last updated on 13/Oct/19

$$2^6=64\Rightarrow \sqrt[6]{-64}=2\mathrm{i}$$

Commented by MJS last updated on 14/Oct/19

$$\mathrm{this}\mathrm{depends}\mathrm{on}\mathrm{what}\mathrm{you}\mathrm{have}\mathrm{already}$$$$\mathrm{learned}.$$$$\mathrm{usually}\mathrm{first}\mathrm{we}\mathrm{learn}\sqrt[3]{-r}=-\sqrt[3]{r}\mathrm{\forall }r\in {\mathbb{R}}^{+}$$$$\mathrm{generally}\sqrt[2n+1]{-r}=-\sqrt[2n+1]{r}\mathrm{\forall }n\in \mathbb{Z}\mathrm{\forall }r\in {\mathbb{R}}^{+}$$$$\mathrm{which}\mathrm{indeed}\mathrm{is}\mathrm{the}\mathrm{only}\mathrm{exception}\mathrm{of}\mathrm{the}$$$$\mathrm{rule}\sqrt[n]{z}=\sqrt[n]{r{\mathrm{e}}^{\mathrm{i}\theta }}=\sqrt[n]{r}{\mathrm{e}}^{\mathrm{i}\frac{\theta }{n}}\mathrm{in}\mathbb{C}$$$$$$$$\mathrm{without}\mathrm{this}\mathrm{rule}$$$$\sqrt[6]{-64}=\sqrt[2]{\sqrt[3]{-64}}=\sqrt[2]{-4}=2\mathrm{i}$$$$[\mathrm{not}\sqrt[6]{-64}=\sqrt[3]{\sqrt[2]{-64}}=\sqrt[3]{8\mathrm{i}}\mathrm{which}{\mathrm{can}}^{\prime }\mathrm{t}\mathrm{be}$$$$\mathrm{solved}\mathrm{on}\mathrm{this}\mathrm{stage}]$$$$$$$$\mathrm{within}\mathrm{this}\mathrm{rule}$$$$\sqrt[6]{-64}=\sqrt[6]{{64\mathrm{e}}^{\mathrm{i}\pi }}=\sqrt[6]{64}{\mathrm{e}}^{\mathrm{i}\frac{\pi }{6}}={2\mathrm{e}}^{\mathrm{i}\frac{\pi }{6}}=\sqrt{3}+\mathrm{i}$$

Answered by Kunal12588 last updated on 14/Oct/19

$${(-1)}^{1/6}\times {\left(2^6\right)}^{1/6}=i^{1/3}\times 2=?$$

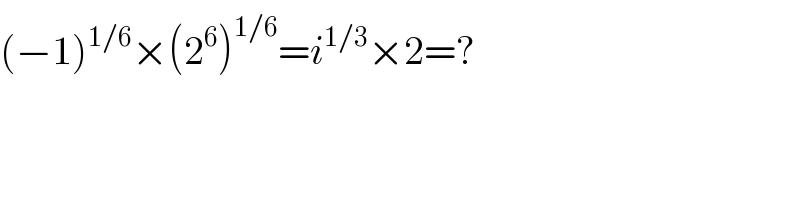
Commented by MJS last updated on 14/Oct/19

$${\mathrm{i}}^{1/3}={\left({\mathrm{e}}^{\mathrm{i}\frac{\pi }{2}}\right)}^{1/3}={\mathrm{e}}^{\mathrm{i}\frac{\pi }{6}}=\frac{\sqrt{3}}{2}+\frac{1}{2}\mathrm{i}$$$$\mathrm{and}{\mathrm{i}}^{1/3}\ne \frac{1}{{\mathrm{i}}^3}$$$$[{\mathrm{z}}^{\frac{1}{3}}=\frac{1}{{\mathrm{z}}^3}\iff z^{\frac{1}{3}}{z}^3=1\iff z^{\frac{4}{3}}=1\iff z=1]$$

Commented by Kunal12588 last updated on 14/Oct/19

ahhh, why they are so complex. yes because they are complex numbers! thanks sir.

Terms of Service

Privacy Policy

Contact: info@tinkutara.com