Question and Answers Forum
Question Number 71406 by mind is power last updated on 15/Oct/19
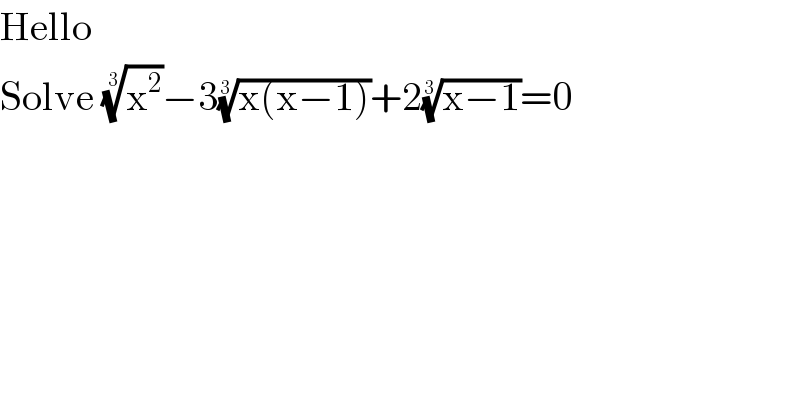
Commented by Prithwish sen last updated on 15/Oct/19

Commented by MJS last updated on 15/Oct/19

Commented by Prithwish sen last updated on 15/Oct/19
Commented by mind is power last updated on 15/Oct/19
Commented by MJS last updated on 15/Oct/19
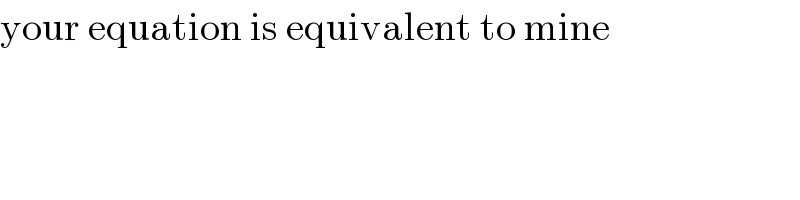
Commented by mind is power last updated on 15/Oct/19