Question Number 71423 by ajfour last updated on 15/Oct/19
Commented by ajfour last updated on 15/Oct/19
$${MjS}\:{Sir}... \\ $$
Commented by mr W last updated on 15/Oct/19
$${such}\:{that}\:{incircle}\:{exists}, \\ $$$${a}+{c}={b}+{d} \\ $$
Commented by MJS last updated on 15/Oct/19
$$\mathrm{I}'\mathrm{ll}\:\mathrm{try}... \\ $$
Commented by ajfour last updated on 15/Oct/19
$${granted},\:{d}={a}+{c}−{b} \\ $$$${find}\:{r}_{{max}} \:{in}\:{terms}\:{of}\:{a},{b},{c}\: \\ $$$${dear}\:{Sir}. \\ $$
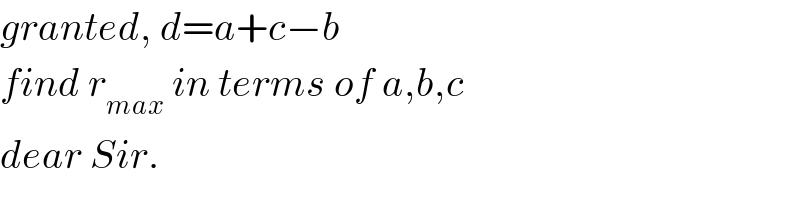
Commented by ajfour last updated on 15/Oct/19
Commented by ajfour last updated on 16/Oct/19
![let φ=∠AEB Area of quad=(r/2)(a+b+c+d) = r(a+c) [As a+c=b+d] =(1/2)absin 2θ+(1/2)c(a+c−b)sin 2φ ......(i) (φ=∠AEB) AB^2 = a^2 +b^2 −2abcos 2θ = c^2 +(a+c−b)^2 −2c(a+c−b)cos 2φ differentiating we get absin 2θ=c(a+c−b)(sin 2φ)(dφ/dθ) and differentiating (i) (a+c)(dr/dθ)=abcos 2θ +c(a+c−b)(cos 2φ)(dφ/dθ) ⇒ for (dr/dθ)=0 abcos 2θ=−c(a+c−b)cos 2φ ×((absin 2θ)/(c(a+c−b)sin 2φ)) ⇒ tan 2φ=−tan 2θ hence (a+c)r=(1/2)[ab+c(a+c−b)]sin 2θ & AB^2 = a^2 +b^2 −2abcos 2θ = c^2 +(a+c−b)^2 +2c(a+c−b)cos 2θ ⇒ cos 2θ=((a^2 +b^2 −c^2 −(a+c−b)^2 )/(2[ab+c(a+c−b)])) r_(max) = (([ab+c(a+c−b)]sin 2θ)/(2(a+c))) r_(max) =(([ab+c(a+c−b)])/(2(a+c)))(√(1−{((a^2 +b^2 −c^2 −(a+c−b)^2 )/(2[ab+c(a+c−b)]))}^2 )) .](Q71484.png)
$$\:{let}\:\:\phi=\angle{AEB} \\ $$$${Area}\:{of}\:{quad}=\frac{{r}}{\mathrm{2}}\left({a}+{b}+{c}+{d}\right) \\ $$$$\:\:\:\:=\:{r}\left({a}+{c}\right)\:\:\:\:\:\:\:\:\:\left[{As}\:{a}+{c}={b}+{d}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ab}\mathrm{sin}\:\mathrm{2}\theta+\frac{\mathrm{1}}{\mathrm{2}}{c}\left({a}+{c}−{b}\right)\mathrm{sin}\:\mathrm{2}\phi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:......\left({i}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\phi=\angle{AEB}\right) \\ $$$$\:{AB}^{\mathrm{2}} =\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\mathrm{cos}\:\mathrm{2}\theta \\ $$$$\:\:=\:{c}^{\mathrm{2}} +\left({a}+{c}−{b}\right)^{\mathrm{2}} −\mathrm{2}{c}\left({a}+{c}−{b}\right)\mathrm{cos}\:\mathrm{2}\phi \\ $$$${differentiating}\:{we}\:{get} \\ $$$$\:{ab}\mathrm{sin}\:\mathrm{2}\theta={c}\left({a}+{c}−{b}\right)\left(\mathrm{sin}\:\mathrm{2}\phi\right)\frac{{d}\phi}{{d}\theta} \\ $$$${and}\:{differentiating}\:\left({i}\right) \\ $$$$\:\:\left({a}+{c}\right)\frac{{dr}}{{d}\theta}={ab}\mathrm{cos}\:\mathrm{2}\theta \\ $$$$\:\:\:\:\:\:+{c}\left({a}+{c}−{b}\right)\left(\mathrm{cos}\:\mathrm{2}\phi\right)\frac{{d}\phi}{{d}\theta}\:\:\:\:\Rightarrow \\ $$$$\:{for}\:\:\frac{{dr}}{{d}\theta}=\mathrm{0} \\ $$$$\:\:{ab}\mathrm{cos}\:\mathrm{2}\theta=−{c}\left({a}+{c}−{b}\right)\mathrm{cos}\:\mathrm{2}\phi \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:×\frac{{ab}\mathrm{sin}\:\mathrm{2}\theta}{{c}\left({a}+{c}−{b}\right)\mathrm{sin}\:\mathrm{2}\phi} \\ $$$$\Rightarrow\:\:\:\mathrm{tan}\:\mathrm{2}\phi=−\mathrm{tan}\:\mathrm{2}\theta \\ $$$${hence}\:\:\: \\ $$$$\:\:\left({a}+{c}\right){r}=\frac{\mathrm{1}}{\mathrm{2}}\left[{ab}+{c}\left({a}+{c}−{b}\right)\right]\mathrm{sin}\:\mathrm{2}\theta \\ $$$$\& \\ $$$$\:{AB}^{\mathrm{2}} =\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\mathrm{cos}\:\mathrm{2}\theta \\ $$$$\:\:=\:{c}^{\mathrm{2}} +\left({a}+{c}−{b}\right)^{\mathrm{2}} +\mathrm{2}{c}\left({a}+{c}−{b}\right)\mathrm{cos}\:\mathrm{2}\theta \\ $$$$\Rightarrow\:\:\mathrm{cos}\:\mathrm{2}\theta=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} −\left({a}+{c}−{b}\right)^{\mathrm{2}} }{\mathrm{2}\left[{ab}+{c}\left({a}+{c}−{b}\right)\right]} \\ $$$$\:{r}_{{max}} =\:\frac{\left[{ab}+{c}\left({a}+{c}−{b}\right)\right]\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}\left({a}+{c}\right)} \\ $$$$\:{r}_{{max}} =\frac{\left[{ab}+{c}\left({a}+{c}−{b}\right)\right]}{\mathrm{2}\left({a}+{c}\right)}\sqrt{\mathrm{1}−\left\{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} −\left({a}+{c}−{b}\right)^{\mathrm{2}} }{\mathrm{2}\left[{ab}+{c}\left({a}+{c}−{b}\right)\right]}\right\}^{\mathrm{2}} }\:. \\ $$$$ \\ $$
Commented by ajfour last updated on 16/Oct/19
$${say}\:{if}\:{a}={b}={c}={d} \\ $$$$\:{r}_{{max}} =\frac{{a}}{\mathrm{2}}\:\centerdot \\ $$