Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 71508 by Cmr 237 last updated on 16/Oct/19

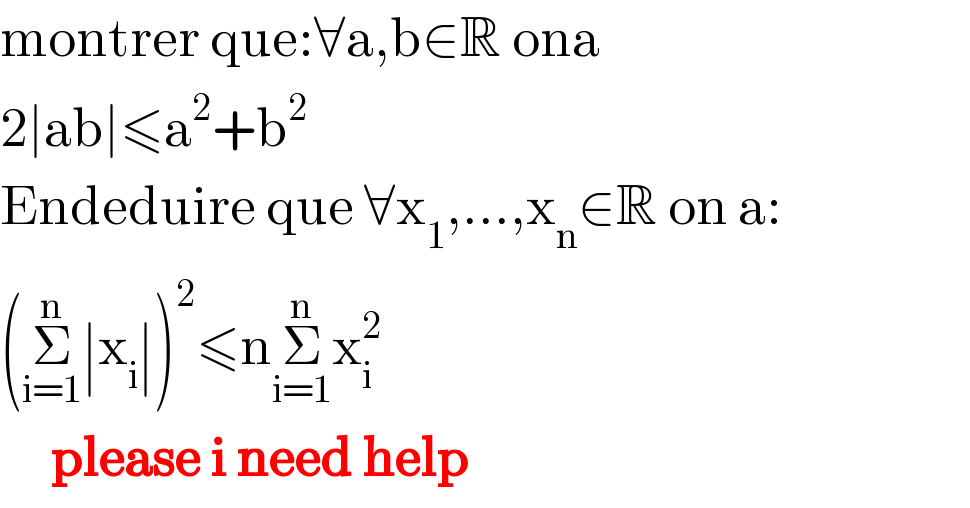
montrer que:∀a,b∈R ona 2∣ab∣≤a^2 +b^2 Endeduire que ∀x_1 ,...,x_n ∈R on a: (Σ_(i=1) ^n ∣x_i ∣)^2 ≤nΣ_(i=1) ^n x_i ^2 please i need help

$$\mathrm{montrer}\:\mathrm{que}:\forall\mathrm{a},\mathrm{b}\in\mathbb{R}\:\mathrm{ona} \\ $$$$\mathrm{2}\mid\mathrm{ab}\mid\leqslant\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \\ $$$$\mathrm{Endeduire}\:\mathrm{que}\:\forall\mathrm{x}_{\mathrm{1}} ,...,\mathrm{x}_{\mathrm{n}} \in\mathbb{R}\:\mathrm{on}\:\mathrm{a}: \\ $$$$\left(\underset{\mathrm{i}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mid\mathrm{x}_{\mathrm{i}} \mid\right)^{\mathrm{2}} \leqslant\mathrm{n}\underset{\mathrm{i}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{x}_{\mathrm{i}} ^{\mathrm{2}} \\ $$$$\:\:\:\:\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{i}}\:\boldsymbol{\mathrm{need}}\:\boldsymbol{\mathrm{help}} \\ $$

Commented by Cmr 237 last updated on 16/Oct/19

please can you prove it?

$$\mathrm{please}\:\mathrm{can}\:\mathrm{you}\:\mathrm{prove}\:\mathrm{it}? \\ $$

Commented by Prithwish sen last updated on 16/Oct/19

let k= ((x_1 +x_2 +.......x_n )/n) .....(i) now (x_1 /k),(x_2 /k),........(x_n /k) all are positive and not all of them equal to 1 [(x_i /k)]^2 −1≥0 equality holds only (x_i /k) = 1 (i∈N) now [(x_1 /k)]^2 +[(x_2 /k)]^2 +.....[(x_n /k)]^2 −n ≥ 2[(x_1 /k)+(x_2 /k)+.....+(x_n /k)−n] (from given condition) or, ((x_1 ^2 +x_2 ^2 +.... +x_n ^2 )/k^2 ) −n ≥ 2(n−n) from (i) or ((x_1 ^2 +x_2 ^2 +.......+x_n ^2 )/n) ≥ k^2 ⇒ x_1 ^2 +x_2 ^2 +......+x_n ^2 ≥ n(((x_1 +x_2 +.....+x_n )/n))^2 ⇒n𝚺_1 ^n (x_i )^2 ≥ (𝚺_1 ^n x_i )^2 Hence proved.

$$\boldsymbol{\mathrm{let}} \\ $$$$\boldsymbol{\mathrm{k}}=\:\frac{\boldsymbol{\mathrm{x}}_{\mathrm{1}} +\boldsymbol{\mathrm{x}}_{\mathrm{2}} +.......\boldsymbol{\mathrm{x}}_{\boldsymbol{\mathrm{n}}} }{\boldsymbol{\mathrm{n}}}\:.....\left(\boldsymbol{\mathrm{i}}\right) \\ $$$$\mathrm{now}\:\frac{\mathrm{x}_{\mathrm{1}} }{\mathrm{k}},\frac{\mathrm{x}_{\mathrm{2}} }{\mathrm{k}},........\frac{\mathrm{x}_{\mathrm{n}} }{\mathrm{k}}\:\mathrm{all}\:\mathrm{are}\:\mathrm{positive}\:\mathrm{and}\:\mathrm{not}\:\mathrm{all} \\ $$$$\mathrm{of}\:\mathrm{them}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{1} \\ $$$$\left[\frac{\boldsymbol{\mathrm{x}}_{\boldsymbol{\mathrm{i}}} }{\boldsymbol{\mathrm{k}}}\right]^{\mathrm{2}} −\mathrm{1}\geqslant\mathrm{0}\:\:\mathrm{equality}\:\mathrm{holds}\:\mathrm{only}\:\frac{\mathrm{x}_{\mathrm{i}} }{\mathrm{k}}\:=\:\mathrm{1}\:\:\left(\mathrm{i}\in\mathbb{N}\right)\: \\ $$$$\mathrm{now}\:\left[\frac{\mathrm{x}_{\mathrm{1}} }{\mathrm{k}}\right]^{\mathrm{2}} +\left[\frac{\mathrm{x}_{\mathrm{2}} }{\mathrm{k}}\right]^{\mathrm{2}} +.....\left[\frac{\mathrm{x}_{\mathrm{n}} }{\mathrm{k}}\right]^{\mathrm{2}} −\mathrm{n}\:\geqslant\:\mathrm{2}\left[\frac{\mathrm{x}_{\mathrm{1}} }{\mathrm{k}}+\frac{\mathrm{x}_{\mathrm{2}} }{\mathrm{k}}+.....+\frac{\mathrm{x}_{\mathrm{n}} }{\mathrm{k}}−\mathrm{n}\right]\:\:\left(\boldsymbol{\mathrm{from}}\:\boldsymbol{\mathrm{given}}\:\boldsymbol{\mathrm{condition}}\right) \\ $$$$\mathrm{or},\:\frac{\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{x}_{\mathrm{2}} ^{\mathrm{2}} +....\:+\mathrm{x}_{\mathrm{n}} ^{\mathrm{2}} }{\mathrm{k}^{\mathrm{2}} }\:−\mathrm{n}\:\geqslant\:\mathrm{2}\left(\mathrm{n}−\mathrm{n}\right)\:\:\boldsymbol{\mathrm{from}}\:\left(\boldsymbol{\mathrm{i}}\right) \\ $$$$\boldsymbol{\mathrm{or}}\:\frac{\boldsymbol{\mathrm{x}}_{\mathrm{1}} ^{\mathrm{2}} +\boldsymbol{\mathrm{x}}_{\mathrm{2}} ^{\mathrm{2}} +.......+\boldsymbol{\mathrm{x}}_{\boldsymbol{\mathrm{n}}} ^{\mathrm{2}} }{\boldsymbol{\mathrm{n}}}\:\geqslant\:\boldsymbol{\mathrm{k}}^{\mathrm{2}} \\ $$$$\Rightarrow\:\boldsymbol{\mathrm{x}}_{\mathrm{1}} ^{\mathrm{2}} +\boldsymbol{\mathrm{x}}_{\mathrm{2}} ^{\mathrm{2}} +......+\boldsymbol{\mathrm{x}}_{\boldsymbol{\mathrm{n}}} ^{\mathrm{2}} \:\geqslant\:\mathrm{n}\left(\frac{\mathrm{x}_{\mathrm{1}} +\mathrm{x}_{\mathrm{2}} +.....+\mathrm{x}_{\mathrm{n}} }{\mathrm{n}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\boldsymbol{\mathrm{n}}\underset{\mathrm{1}} {\overset{\boldsymbol{\mathrm{n}}} {\boldsymbol{\sum}}}\left(\boldsymbol{\mathrm{x}}_{\boldsymbol{\mathrm{i}}} \right)^{\mathrm{2}} \geqslant\:\left(\underset{\mathrm{1}} {\overset{\boldsymbol{\mathrm{n}}} {\boldsymbol{\sum}}\mathrm{x}}_{\boldsymbol{\mathrm{i}}} \:\right)^{\mathrm{2}} \:\:\boldsymbol{\mathrm{Hence}}\:\boldsymbol{\mathrm{proved}}. \\ $$

Answered by turbo msup by abdo last updated on 17/Oct/19

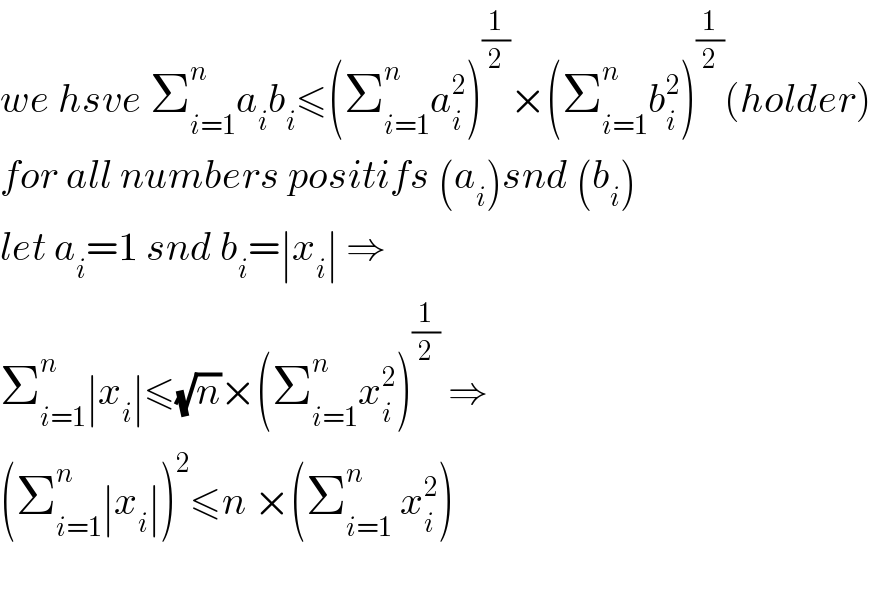
we hsve Σ_(i=1) ^n a_i b_i ≤(Σ_(i=1) ^n a_i ^2 )^(1/2) ×(Σ_(i=1) ^n b_i ^2 )^(1/2) (holder) for all numbers positifs (a_i )snd (b_i ) let a_i =1 snd b_i =∣x_i ∣ ⇒ Σ_(i=1) ^n ∣x_i ∣≤(√n)×(Σ_(i=1) ^n x_i ^2 )^(1/2) ⇒ (Σ_(i=1) ^n ∣x_i ∣)^2 ≤n ×(Σ_(i=1) ^n x_i ^2 )

$${we}\:{hsve}\:\sum_{{i}=\mathrm{1}} ^{{n}} {a}_{{i}} {b}_{{i}} \leqslant\left(\sum_{{i}=\mathrm{1}} ^{{n}} {a}_{{i}} ^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} ×\left(\sum_{{i}=\mathrm{1}} ^{{n}} {b}_{{i}} ^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \left({holder}\right) \\ $$$${for}\:{all}\:{numbers}\:{positifs}\:\left({a}_{{i}} \right){snd}\:\left({b}_{{i}} \right) \\ $$$${let}\:{a}_{{i}} =\mathrm{1}\:{snd}\:{b}_{{i}} =\mid{x}_{{i}} \mid\:\Rightarrow \\ $$$$\sum_{{i}=\mathrm{1}} ^{{n}} \mid{x}_{{i}} \mid\leqslant\sqrt{{n}}×\left(\sum_{{i}=\mathrm{1}} ^{{n}} {x}_{{i}} ^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:\Rightarrow \\ $$$$\left(\sum_{{i}=\mathrm{1}} ^{{n}} \mid{x}_{{i}} \mid\right)^{\mathrm{2}} \leqslant{n}\:×\left(\sum_{{i}=\mathrm{1}} ^{{n}} \:{x}_{{i}} ^{\mathrm{2}} \right) \\ $$$$ \\ $$

Commented by Prithwish sen last updated on 17/Oct/19

Thank you sir.

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by mathmax by abdo last updated on 18/Oct/19

you are welcome.

$${you}\:{are}\:{welcome}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com