Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 7161 by Tawakalitu. last updated on 14/Aug/16

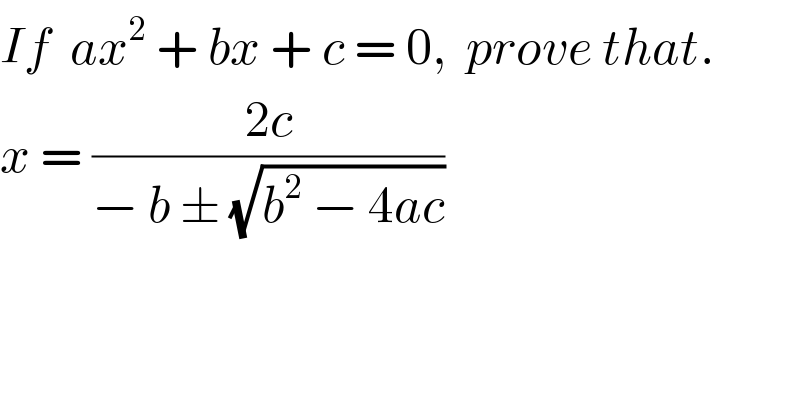
If ax^2 + bx + c = 0, prove that. x = ((2c)/(− b ± (√(b^2 − 4ac))))

$${If}\:\:{ax}^{\mathrm{2}} \:+\:{bx}\:+\:{c}\:=\:\mathrm{0},\:\:{prove}\:{that}. \\ $$$${x}\:=\:\frac{\mathrm{2}{c}}{−\:{b}\:\pm\:\sqrt{{b}^{\mathrm{2}} \:−\:\mathrm{4}{ac}}}\: \\ $$

Commented by sou1618 last updated on 14/Aug/16

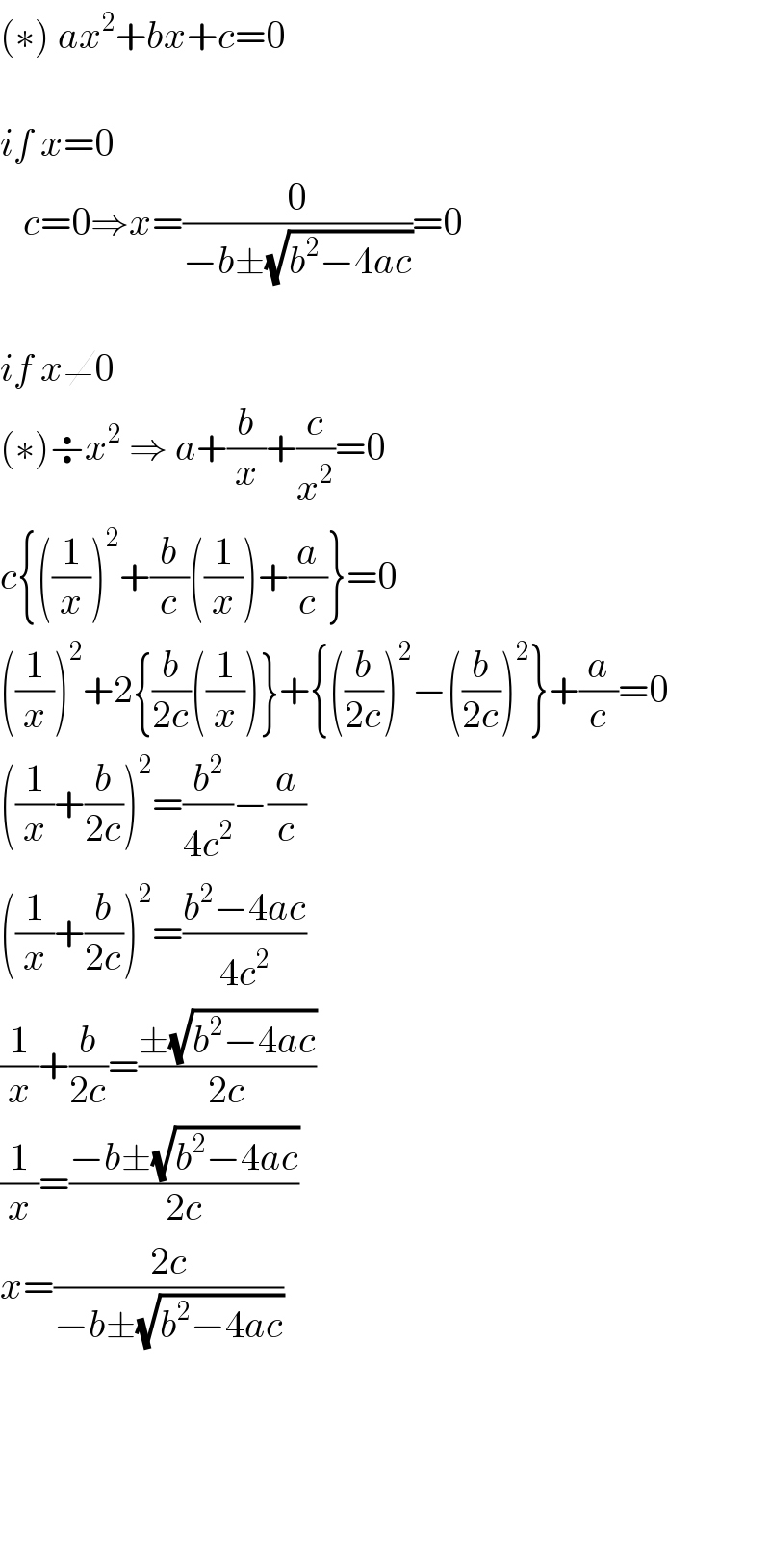
(∗) ax^2 +bx+c=0 if x=0 c=0⇒x=(0/(−b±(√(b^2 −4ac))))=0 if x≠0 (∗)÷x^2 ⇒ a+(b/x)+(c/x^2 )=0 c{((1/x))^2 +(b/c)((1/x))+(a/c)}=0 ((1/x))^2 +2{(b/(2c))((1/x))}+{((b/(2c)))^2 −((b/(2c)))^2 }+(a/c)=0 ((1/x)+(b/(2c)))^2 =(b^2 /(4c^2 ))−(a/c) ((1/x)+(b/(2c)))^2 =((b^2 −4ac)/(4c^2 )) (1/x)+(b/(2c))=((±(√(b^2 −4ac)))/(2c)) (1/x)=((−b±(√(b^2 −4ac)))/(2c)) x=((2c)/(−b±(√(b^2 −4ac))))

$$\left(\ast\right)\:{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$$ \\ $$$${if}\:{x}=\mathrm{0} \\ $$$$\:\:\:{c}=\mathrm{0}\Rightarrow{x}=\frac{\mathrm{0}}{−{b}\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}=\mathrm{0} \\ $$$$ \\ $$$${if}\:{x}\neq\mathrm{0} \\ $$$$\left(\ast\right)\boldsymbol{\div}{x}^{\mathrm{2}} \:\Rightarrow\:{a}+\frac{{b}}{{x}}+\frac{{c}}{{x}^{\mathrm{2}} }=\mathrm{0} \\ $$$${c}\left\{\left(\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\frac{{b}}{{c}}\left(\frac{\mathrm{1}}{{x}}\right)+\frac{{a}}{{c}}\right\}=\mathrm{0} \\ $$$$\left(\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{2}\left\{\frac{{b}}{\mathrm{2}{c}}\left(\frac{\mathrm{1}}{{x}}\right)\right\}+\left\{\left(\frac{{b}}{\mathrm{2}{c}}\right)^{\mathrm{2}} −\left(\frac{{b}}{\mathrm{2}{c}}\right)^{\mathrm{2}} \right\}+\frac{{a}}{{c}}=\mathrm{0} \\ $$$$\left(\frac{\mathrm{1}}{{x}}+\frac{{b}}{\mathrm{2}{c}}\right)^{\mathrm{2}} =\frac{{b}^{\mathrm{2}} }{\mathrm{4}{c}^{\mathrm{2}} }−\frac{{a}}{{c}} \\ $$$$\left(\frac{\mathrm{1}}{{x}}+\frac{{b}}{\mathrm{2}{c}}\right)^{\mathrm{2}} =\frac{{b}^{\mathrm{2}} −\mathrm{4}{ac}}{\mathrm{4}{c}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{{b}}{\mathrm{2}{c}}=\frac{\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{\mathrm{2}{c}} \\ $$$$\frac{\mathrm{1}}{{x}}=\frac{−{b}\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{\mathrm{2}{c}} \\ $$$${x}=\frac{\mathrm{2}{c}}{−{b}\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by aftab ahmad last updated on 14/Aug/16

Nice approach sir.

$$\boldsymbol{{N}}{ice}\:{approach}\:{sir}.\: \\ $$

Commented by Tawakalitu. last updated on 14/Aug/16

Thanks so much sir. i really appreciate.

$${Thanks}\:{so}\:{much}\:{sir}.\:{i}\:{really}\:{appreciate}. \\ $$

Answered by Yozzia last updated on 14/Aug/16

ax^2 +bx+c=0 (a≠0) ⇒x=((−b±(√(b^2 −4ac)))/(2a)) x=(((−b±(√(b^2 −4ac)))(−b∓(√(b^2 −4ac))))/(2a(−b∓(√(b^2 −4ac))))) x=((b^2 −b^2 +4ac)/(2a(−b∓(√(b^2 −4ac))))) x=((4ac)/(2a(−b∓(√(b^2 −4ac)))))=((2c)/(−b∓(√(b^2 −4ac)))) This is equivalent to x=((2c)/(−b±(√(b^2 −4ac)))).

$${ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0}\:\:\:\left({a}\neq\mathrm{0}\right) \\ $$$$\Rightarrow{x}=\frac{−{b}\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}{\mathrm{2}{a}} \\ $$$${x}=\frac{\left(−{b}\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}\right)\left(−{b}\mp\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}\right)}{\mathrm{2}{a}\left(−{b}\mp\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}\right)} \\ $$$${x}=\frac{{b}^{\mathrm{2}} −{b}^{\mathrm{2}} +\mathrm{4}{ac}}{\mathrm{2}{a}\left(−{b}\mp\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}\right)} \\ $$$${x}=\frac{\mathrm{4}{ac}}{\mathrm{2}{a}\left(−{b}\mp\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}\right)}=\frac{\mathrm{2}{c}}{−{b}\mp\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}} \\ $$$${This}\:{is}\:{equivalent}\:{to}\: \\ $$$${x}=\frac{\mathrm{2}{c}}{−{b}\pm\sqrt{{b}^{\mathrm{2}} −\mathrm{4}{ac}}}. \\ $$$$ \\ $$$$ \\ $$

Commented by Tawakalitu. last updated on 14/Aug/16

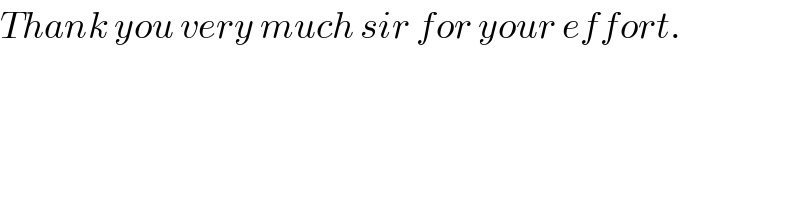
Thank you very much sir for your effort.

$${Thank}\:{you}\:{very}\:{much}\:{sir}\:{for}\:{your}\:{effort}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com