
Question and Answers Forum
Question Number 71739 by Tony Lin last updated on 19/Oct/19
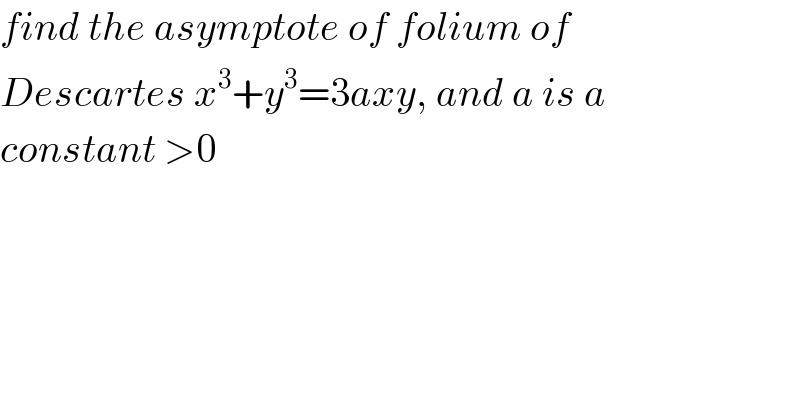
Answered by Tony Lin last updated on 19/Oct/19
![let y=tx ⇒x^3 +(tx)^3 =3atx^2 { ((x=((3at)/(1+t^3 )))),((y=((3at^2 )/(1+t^3 )))) :} x→±∞⇒t→−1 let the asymptote L: mx+b lim_(t→−1) (y/x)=−1=m lim_(t→−1) [y−(−x)] =lim_(x→−1) ((3at(t+1))/((t+1)(t^2 −t+1))) =−a =b therefore asymptote L:−x−a](Q71760.png)
Answered by MJS last updated on 19/Oct/19

Commented byMJS last updated on 19/Oct/19

| ||
Question and Answers Forum | ||
Question Number 71739 by Tony Lin last updated on 19/Oct/19 | ||
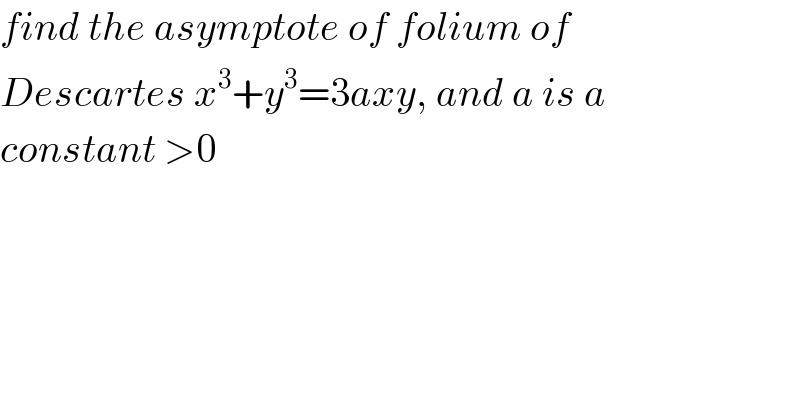 | ||
Answered by Tony Lin last updated on 19/Oct/19 | ||
![let y=tx ⇒x^3 +(tx)^3 =3atx^2 { ((x=((3at)/(1+t^3 )))),((y=((3at^2 )/(1+t^3 )))) :} x→±∞⇒t→−1 let the asymptote L: mx+b lim_(t→−1) (y/x)=−1=m lim_(t→−1) [y−(−x)] =lim_(x→−1) ((3at(t+1))/((t+1)(t^2 −t+1))) =−a =b therefore asymptote L:−x−a](Q71760.png) | ||
| ||
Answered by MJS last updated on 19/Oct/19 | ||
 | ||
| ||
Commented byMJS last updated on 19/Oct/19 | ||
 | ||