Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 71814 by Aman Arya last updated on 20/Oct/19

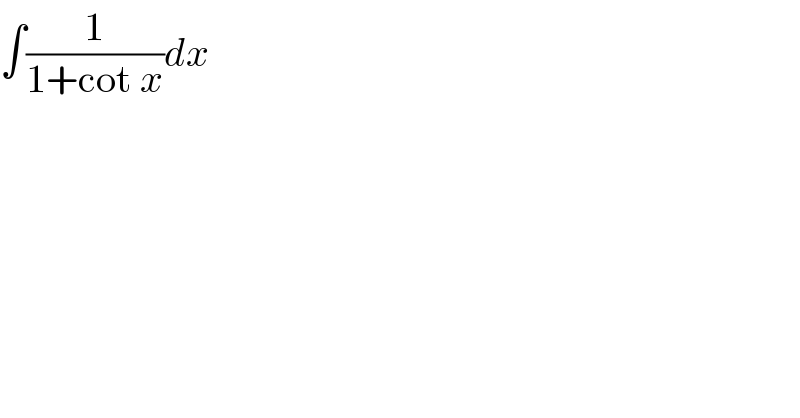
∫(1/(1+cot x))dx

$$\int\frac{\mathrm{1}}{\mathrm{1}+\mathrm{cot}\:{x}}{dx} \\ $$

Commented by mathmax by abdo last updated on 20/Oct/19

let I=∫ (dx/(1+cotanx)) ⇒I=∫ (dx/(1+((cosx)/(sinx)))) =∫((sinx)/(sinx +cosx))dx changement tan((x/2))=t give I=∫ (((2t)/(1+t^2 ))/(((2t)/(1+t^2 ))+((1−t^2 )/(1+t^2 ))))((2dt)/(1+t^2 )) I=∫ ((2t)/((1+t^2 )^2 {((2t)/(1+t^2 ))+((1−t^2 )/(1+t^2 ))}))dt =∫ ((2t)/((1+t^2 )(−t^2 +2t+1)))dt =−2∫(t/((t^2 +1)(t^2 −2t−1)))dt let decompose F(t)=(t/((t^2 +1)(t^2 −2t−1))) t^2 −2t−1=0→Δ^′ =1+1=2 ⇒t_1 =1+(√2) and t_2 =1−(√2) F(t)=(t/((t−t_1 )(t−t_2 )(t^2 +1))) =(a/(t−t_1 )) +(b/(t−t_2 )) +((ct +d)/(t^2 +1)) a=lim_(t→t_1 ) (t−t_1 )F(t)=(t_1 /((t_1 −t_2 )(t_1 ^2 +1))) =((1+(√2))/(2(√2)(3+2(√2)+1))) =((2+(√2))/(4(4+2(√2)))) =((2+(√2))/(8(2+(√2)))) =(1/8) b=(t_2 /((t_2 −t_1 )(t_2 ^2 +1))) =((1−(√2))/((−2(√2))(3−2(√2)+1))) =((−1+(√2))/(2(√2)(4−2(√2)))) =((−(√2)+2)/(8(2−(√2)))) =(1/8) lim_(t→+∞) tF(t)=0=a+b+c ⇒c=−a−b =−(1/4) ⇒ F(t)=(1/(8(t−t_1 ))) +(1/(8(t−t_2 ))) +((−(1/4)t+d)/(t^2 +1)) F(0)=0 =−(1/(8t_1 ))−(1/(8t_2 )) +d ⇒d=(1/8)((1/t_1 )+(1/t_2 ))=(1/8)(((t_1 +t_2 )/(t_1 t_2 ))) =(1/8)(2/(−1)) =−(1/4) ⇒F(t)=(1/(8(t−t_1 ))) +(1/(8(t−t_2 )))−(1/4) ((t+1)/(t^2 +1)) ⇒ I =−(1/4)∫ (dt/(t−t_1 ))−(1/4)∫ (dt/(t−t_2 )) +(1/2)∫ ((t+1)/(t^2 +1))dt =−(1/4)ln∣t−t_1 ∣−(1/4)ln∣t−t_2 ∣+(1/4)ln(t^2 +1) +(1/2)arctant +c =−(1/4)ln∣tan((x/2))−1−(√2)∣−(1/4)ln∣tan((x/2))−1+(√2)∣ +(1/4)ln(1+tan^2 ((x/2))) +(x/4) +c .

$${let}\:{I}=\int\:\frac{{dx}}{\mathrm{1}+{cotanx}}\:\Rightarrow{I}=\int\:\frac{{dx}}{\mathrm{1}+\frac{{cosx}}{{sinx}}}\:=\int\frac{{sinx}}{{sinx}\:+{cosx}}{dx} \\ $$$${changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give}\:{I}=\int\:\:\frac{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${I}=\int\:\:\:\:\frac{\mathrm{2}{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} \left\{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right\}}{dt}\:=\int\:\frac{\mathrm{2}{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(−{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}\right)}{dt} \\ $$$$=−\mathrm{2}\int\frac{{t}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)}{dt}\:{let}\:{decompose}\:{F}\left({t}\right)=\frac{{t}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}\right)} \\ $$$${t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}=\mathrm{0}\rightarrow\Delta^{'} =\mathrm{1}+\mathrm{1}=\mathrm{2}\:\Rightarrow{t}_{\mathrm{1}} =\mathrm{1}+\sqrt{\mathrm{2}}\:{and}\:{t}_{\mathrm{2}} =\mathrm{1}−\sqrt{\mathrm{2}} \\ $$$${F}\left({t}\right)=\frac{{t}}{\left({t}−{t}_{\mathrm{1}} \right)\left({t}−{t}_{\mathrm{2}} \right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}\:=\frac{{a}}{{t}−{t}_{\mathrm{1}} }\:+\frac{{b}}{{t}−{t}_{\mathrm{2}} }\:+\frac{{ct}\:+{d}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}={lim}_{{t}\rightarrow{t}_{\mathrm{1}} } \:\:\left({t}−{t}_{\mathrm{1}} \right){F}\left({t}\right)=\frac{{t}_{\mathrm{1}} }{\left({t}_{\mathrm{1}} −{t}_{\mathrm{2}} \right)\left({t}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{\mathrm{2}}\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{4}\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{2}}\right)}\:=\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{8}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)}\:=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$${b}=\frac{{t}_{\mathrm{2}} }{\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)\left({t}_{\mathrm{2}} ^{\mathrm{2}} +\mathrm{1}\right)}\:=\frac{\mathrm{1}−\sqrt{\mathrm{2}}}{\left(−\mathrm{2}\sqrt{\mathrm{2}}\right)\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{1}\right)}\:=\frac{−\mathrm{1}+\sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{\mathrm{2}}\left(\mathrm{4}−\mathrm{2}\sqrt{\mathrm{2}}\right)} \\ $$$$=\frac{−\sqrt{\mathrm{2}}+\mathrm{2}}{\mathrm{8}\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)}\:=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$${lim}_{{t}\rightarrow+\infty} {tF}\left({t}\right)=\mathrm{0}={a}+{b}+{c}\:\Rightarrow{c}=−{a}−{b}\:=−\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$${F}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{8}\left({t}−{t}_{\mathrm{1}} \right)}\:+\frac{\mathrm{1}}{\mathrm{8}\left({t}−{t}_{\mathrm{2}} \right)}\:+\frac{−\frac{\mathrm{1}}{\mathrm{4}}{t}+{d}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)=\mathrm{0}\:=−\frac{\mathrm{1}}{\mathrm{8}{t}_{\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{8}{t}_{\mathrm{2}} }\:+{d}\:\Rightarrow{d}=\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{1}}{{t}_{\mathrm{1}} }+\frac{\mathrm{1}}{{t}_{\mathrm{2}} }\right)=\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{{t}_{\mathrm{1}} +{t}_{\mathrm{2}} }{{t}_{\mathrm{1}} {t}_{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\frac{\mathrm{2}}{−\mathrm{1}}\:=−\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow{F}\left({t}\right)=\frac{\mathrm{1}}{\mathrm{8}\left({t}−{t}_{\mathrm{1}} \right)}\:+\frac{\mathrm{1}}{\mathrm{8}\left({t}−{t}_{\mathrm{2}} \right)}−\frac{\mathrm{1}}{\mathrm{4}}\:\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${I}\:=−\frac{\mathrm{1}}{\mathrm{4}}\int\:\:\frac{{dt}}{{t}−{t}_{\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{{dt}}{{t}−{t}_{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid{t}−{t}_{\mathrm{1}} \mid−\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid{t}−{t}_{\mathrm{2}} \mid+\frac{\mathrm{1}}{\mathrm{4}}{ln}\left({t}^{\mathrm{2}} +\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}{arctant}\:+{c} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid{tan}\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{1}−\sqrt{\mathrm{2}}\mid−\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid{tan}\left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{1}+\sqrt{\mathrm{2}}\mid \\ $$$$+\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)\:+\frac{{x}}{\mathrm{4}}\:+{c}\:. \\ $$

Commented by petrochengula last updated on 21/Oct/19

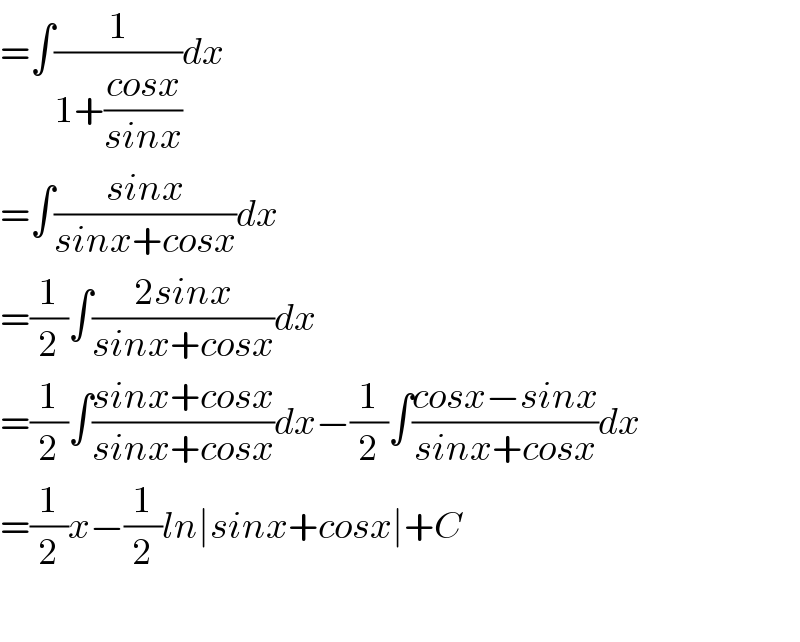
=∫(1/(1+((cosx)/(sinx))))dx =∫((sinx)/(sinx+cosx))dx =(1/2)∫((2sinx)/(sinx+cosx))dx =(1/2)∫((sinx+cosx)/(sinx+cosx))dx−(1/2)∫((cosx−sinx)/(sinx+cosx))dx =(1/2)x−(1/2)ln∣sinx+cosx∣+C

$$=\int\frac{\mathrm{1}}{\mathrm{1}+\frac{{cosx}}{{sinx}}}{dx} \\ $$$$=\int\frac{{sinx}}{{sinx}+{cosx}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}{sinx}}{{sinx}+{cosx}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{sinx}+{cosx}}{{sinx}+{cosx}}{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{cosx}−{sinx}}{{sinx}+{cosx}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{x}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid{sinx}+{cosx}\mid+{C} \\ $$$$ \\ $$

Answered by $@ty@m123 last updated on 20/Oct/19

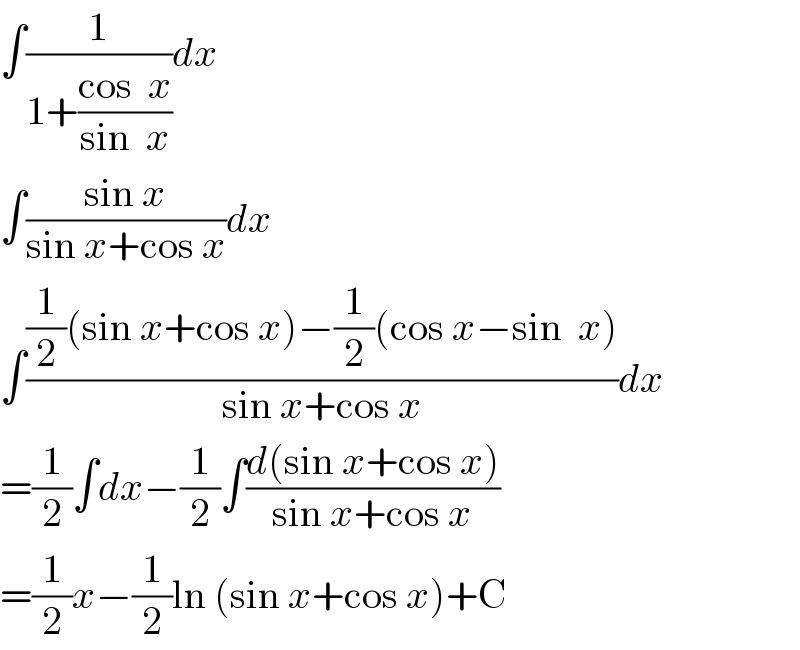
∫(1/(1+((cos x)/(sin x))))dx ∫((sin x)/(sin x+cos x))dx ∫(((1/2)(sin x+cos x)−(1/2)(cos x−sin x))/(sin x+cos x))dx =(1/2)∫dx−(1/2)∫((d(sin x+cos x))/(sin x+cos x)) =(1/2)x−(1/2)ln (sin x+cos x)+C

$$\int\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{cos}\:\:{x}}{\mathrm{sin}\:\:{x}}}{dx} \\ $$$$\int\frac{\mathrm{sin}\:{x}}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{dx} \\ $$$$\int\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{cos}\:{x}−\mathrm{sin}\:\:{x}\right)}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)}{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)+\mathrm{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com