Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 72020 by mathmax by abdo last updated on 23/Oct/19

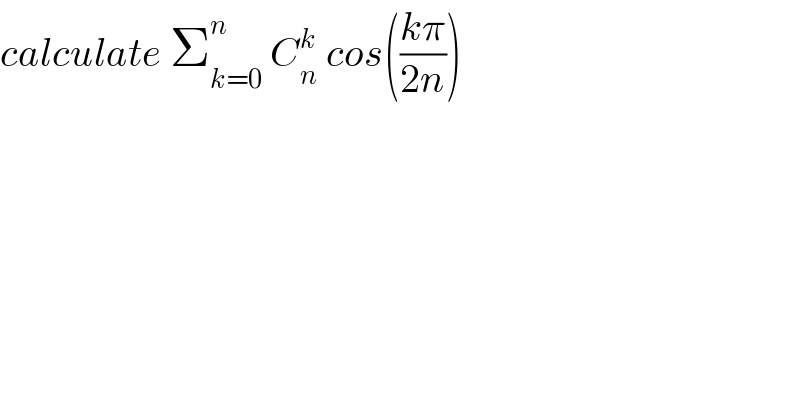
calculate Σ_(k=0) ^n C_n ^k cos(((kπ)/(2n)))

$${calculate}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{cos}\left(\frac{{k}\pi}{\mathrm{2}{n}}\right) \\ $$

Commented by mathmax by abdo last updated on 24/Oct/19

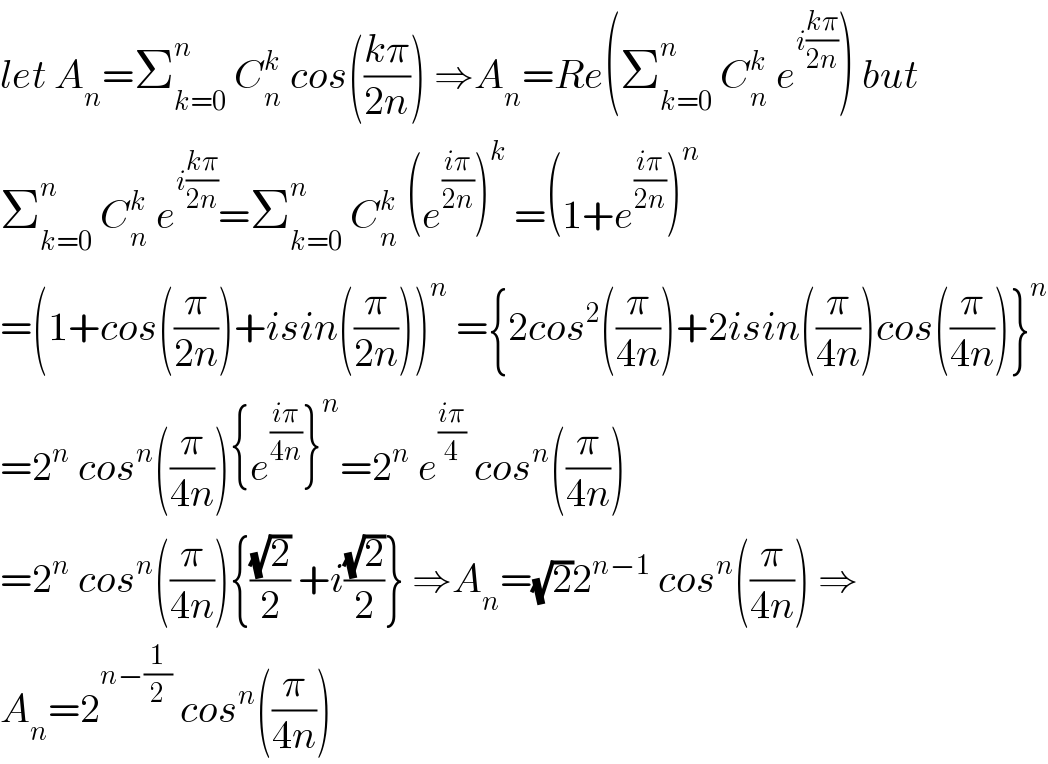
let A_n =Σ_(k=0) ^n C_n ^k cos(((kπ)/(2n))) ⇒A_n =Re(Σ_(k=0) ^n C_n ^k e^(i((kπ)/(2n))) ) but Σ_(k=0) ^n C_n ^k e^(i((kπ)/(2n))) =Σ_(k=0) ^n C_n ^k (e^((iπ)/(2n)) )^k =(1+e^((iπ)/(2n)) )^n =(1+cos((π/(2n)))+isin((π/(2n))))^n ={2cos^2 ((π/(4n)))+2isin((π/(4n)))cos((π/(4n)))}^n =2^n cos^n ((π/(4n))){e^((iπ)/(4n)) }^n =2^n e^((iπ)/4) cos^n ((π/(4n))) =2^n cos^n ((π/(4n))){((√2)/2) +i((√2)/2)} ⇒A_n =(√2)2^(n−1) cos^n ((π/(4n))) ⇒ A_n =2^(n−(1/2)) cos^n ((π/(4n)))

$${let}\:{A}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{cos}\left(\frac{{k}\pi}{\mathrm{2}{n}}\right)\:\Rightarrow{A}_{{n}} ={Re}\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{e}^{{i}\frac{{k}\pi}{\mathrm{2}{n}}} \right)\:{but} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:{e}^{{i}\frac{{k}\pi}{\mathrm{2}{n}}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\left({e}^{\frac{{i}\pi}{\mathrm{2}{n}}} \right)^{{k}} \:=\left(\mathrm{1}+{e}^{\frac{{i}\pi}{\mathrm{2}{n}}} \right)^{{n}} \\ $$$$=\left(\mathrm{1}+{cos}\left(\frac{\pi}{\mathrm{2}{n}}\right)+{isin}\left(\frac{\pi}{\mathrm{2}{n}}\right)\right)^{{n}} \:=\left\{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}{n}}\right)+\mathrm{2}{isin}\left(\frac{\pi}{\mathrm{4}{n}}\right){cos}\left(\frac{\pi}{\mathrm{4}{n}}\right)\right\}^{{n}} \\ $$$$=\mathrm{2}^{{n}} \:{cos}^{{n}} \left(\frac{\pi}{\mathrm{4}{n}}\right)\left\{{e}^{\frac{{i}\pi}{\mathrm{4}{n}}} \right\}^{{n}} =\mathrm{2}^{{n}} \:{e}^{\frac{{i}\pi}{\mathrm{4}}} \:{cos}^{{n}} \left(\frac{\pi}{\mathrm{4}{n}}\right) \\ $$$$=\mathrm{2}^{{n}} \:{cos}^{{n}} \left(\frac{\pi}{\mathrm{4}{n}}\right)\left\{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:+{i}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right\}\:\Rightarrow{A}_{{n}} =\sqrt{\mathrm{2}}\mathrm{2}^{{n}−\mathrm{1}} \:{cos}^{{n}} \left(\frac{\pi}{\mathrm{4}{n}}\right)\:\Rightarrow \\ $$$${A}_{{n}} =\mathrm{2}^{{n}−\frac{\mathrm{1}}{\mathrm{2}}} \:{cos}^{{n}} \left(\frac{\pi}{\mathrm{4}{n}}\right) \\ $$

Answered by mind is power last updated on 23/Oct/19

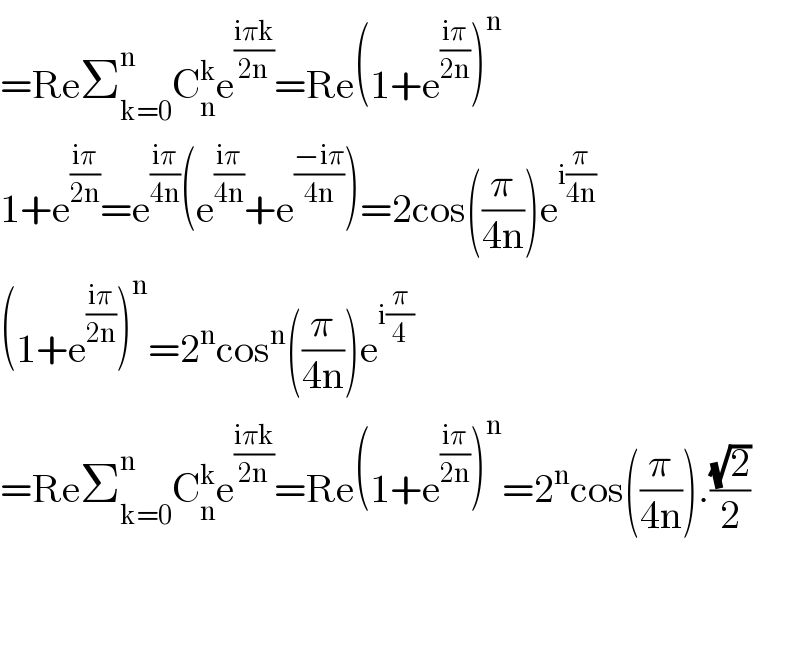
=ReΣ_(k=0) ^n C_n ^k e^((iπk)/(2n)) =Re(1+e^((iπ)/(2n)) )^n 1+e^((iπ)/(2n)) =e^((iπ)/(4n)) (e^((iπ)/(4n)) +e^((−iπ)/(4n)) )=2cos((π/(4n)))e^(i(π/(4n))) (1+e^((iπ)/(2n)) )^n =2^n cos^n ((π/(4n)))e^(i(π/4)) =ReΣ_(k=0) ^n C_n ^k e^((iπk)/(2n)) =Re(1+e^((iπ)/(2n)) )^n =2^n cos((π/(4n))).((√2)/2)

$$=\mathrm{Re}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \mathrm{e}^{\frac{\mathrm{i}\pi\mathrm{k}}{\mathrm{2n}}} =\mathrm{Re}\left(\mathrm{1}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{2n}}} \right)^{\mathrm{n}} \\ $$$$\mathrm{1}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{2n}}} =\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4n}}} \left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{4n}}} +\mathrm{e}^{\frac{−\mathrm{i}\pi}{\mathrm{4n}}} \right)=\mathrm{2cos}\left(\frac{\pi}{\mathrm{4n}}\right)\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{4n}}} \\ $$$$\left(\mathrm{1}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{2n}}} \right)^{\mathrm{n}} =\mathrm{2}^{\mathrm{n}} \mathrm{cos}^{\mathrm{n}} \left(\frac{\pi}{\mathrm{4n}}\right)\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{4}}} \\ $$$$=\mathrm{Re}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \mathrm{e}^{\frac{\mathrm{i}\pi\mathrm{k}}{\mathrm{2n}}} =\mathrm{Re}\left(\mathrm{1}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{2n}}} \right)^{\mathrm{n}} =\mathrm{2}^{\mathrm{n}} \mathrm{cos}\left(\frac{\pi}{\mathrm{4n}}\right).\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com