Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 72026 by mathmax by abdo last updated on 23/Oct/19

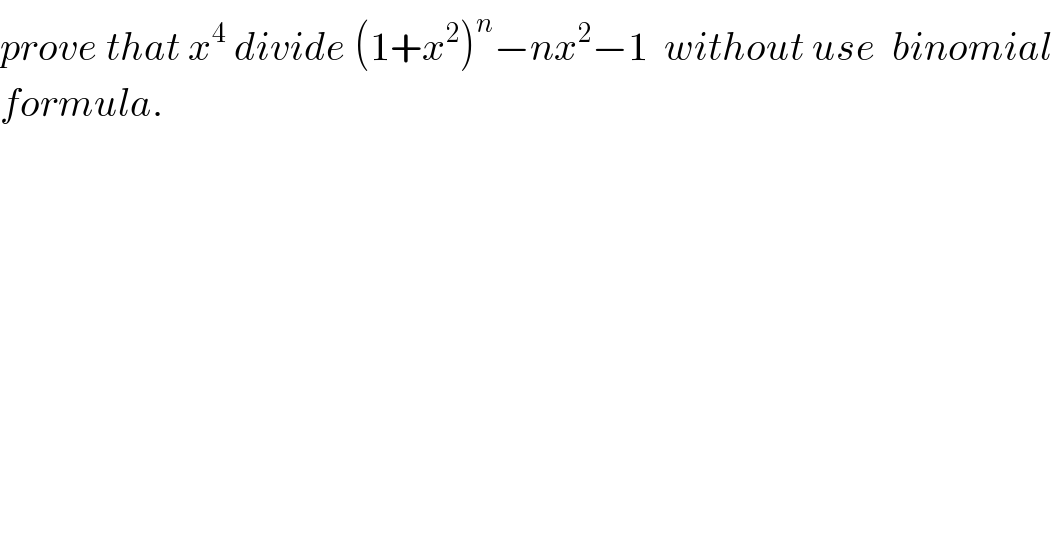
prove that x^4 divide (1+x^2 )^n −nx^2 −1 without use binomial formula.

$${prove}\:{that}\:{x}^{\mathrm{4}} \:{divide}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{{n}} −{nx}^{\mathrm{2}} −\mathrm{1}\:\:{without}\:{use}\:\:{binomial} \\ $$$${formula}. \\ $$

Commented by mathmax by abdo last updated on 24/Oct/19

let P_n (x)=(1+x^2 )^n −nx^2 −1 let prove that x^4 divide P_n (x) by recurrence n=0 ⇒P_n (0)=1−1=0 and x^4 divide 0 let suppose x^4 divide P_n (x) ⇒ ∃ Q ∈R[x] /P_n (x)=x^4 Q(x) we have P_(n+1) (x)=(1+x^2 )^(n+1) −(n+1)x^2 −1 =(1+x^2 )(1+x^2 )^n −(n+1)x^2 −1 =(1+x^2 )(P_n (x)+nx^2 +1)−(n+1)x^2 −1 =(1+x^2 )P_n (x)+nx^2 (1+x^2 )+1+x^2 −nx^2 −x^2 −1 =(1+x^2 )P_n (x)+nx^4 =(1+x^2 )(x^4 Q(x)) +nx^4 =x^4 { (1+x^2 )Q(x) +n} ⇒x^4 divide P_(n+1) (x) so the result is proved.

$${let}\:{P}_{{n}} \left({x}\right)=\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{{n}} −{nx}^{\mathrm{2}} −\mathrm{1}\:{let}\:{prove}\:{that}\:{x}^{\mathrm{4}} \:{divide}\:{P}_{{n}} \left({x}\right) \\ $$$${by}\:{recurrence}\:\:{n}=\mathrm{0}\:\Rightarrow{P}_{{n}} \left(\mathrm{0}\right)=\mathrm{1}−\mathrm{1}=\mathrm{0}\:\:{and}\:{x}^{\mathrm{4}} \:{divide}\:\mathrm{0} \\ $$$${let}\:{suppose}\:{x}^{\mathrm{4}} \:{divide}\:{P}_{{n}} \left({x}\right)\:\Rightarrow\:\exists\:{Q}\:\in{R}\left[{x}\right]\:/{P}_{{n}} \left({x}\right)={x}^{\mathrm{4}} {Q}\left({x}\right) \\ $$$${we}\:{have}\:{P}_{{n}+\mathrm{1}} \left({x}\right)=\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{{n}+\mathrm{1}} −\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} −\mathrm{1} \\ $$$$=\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{{n}} −\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} −\mathrm{1} \\ $$$$=\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left({P}_{{n}} \left({x}\right)+{nx}^{\mathrm{2}} \:+\mathrm{1}\right)−\left({n}+\mathrm{1}\right){x}^{\mathrm{2}} −\mathrm{1} \\ $$$$=\left(\mathrm{1}+{x}^{\mathrm{2}} \right){P}_{{n}} \left({x}\right)+{nx}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)+\mathrm{1}+{x}^{\mathrm{2}} −{nx}^{\mathrm{2}} −{x}^{\mathrm{2}} −\mathrm{1} \\ $$$$=\left(\mathrm{1}+{x}^{\mathrm{2}} \right){P}_{{n}} \left({x}\right)+{nx}^{\mathrm{4}} \:\:=\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left({x}^{\mathrm{4}} {Q}\left({x}\right)\right)\:+{nx}^{\mathrm{4}} \\ $$$$={x}^{\mathrm{4}} \left\{\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right){Q}\left({x}\right)\:+{n}\right\}\:\Rightarrow{x}^{\mathrm{4}} \:{divide}\:{P}_{{n}+\mathrm{1}} \left({x}\right)\:{so}\:{the}\:{result}\:{is} \\ $$$${proved}. \\ $$

Answered by mind is power last updated on 23/Oct/19

(1+x^2 )^n −nx^2 −1 for n=0 ,n=1,n=2 juste evaluate for n≥2 p(x)=(1+x^2 )^n −nx^2 −1 p(0)=0 p′(x)=2xn(1+x^2 )^(n−1) −2nx p′(0)=0 p′′(x)=2n(1+x^2 )^(n−1) +4x^2 n(n−1)(1+x^2 )^(n−2) −2n p′′(0)=2n−2n=0 p′′′(x)=4nx(n−1)(1+x^2 )^(n−2) +8xn(n−1)(1+x^2 )^(n−2) +8x^3 n(n−1)(n−2)(1+x^2 )^(n−3) p′′′(0)=0 taylor formula p(x)=Σ_(k=1) ^(2n) p^((k)) (0).(x^k /(k!))=((x^4 p^((4)) (0))/(4!))+.... =x^4 (.Q(x)) Q(x)=Σ_(k=4) ^(2n) ((p^((k)) x^(k−4) )/(k!)) ⇒X^4 ∣(1+x^2 )^n −nx^2 −1

$$\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}} −\mathrm{nx}^{\mathrm{2}} −\mathrm{1} \\ $$$$\mathrm{for}\:\mathrm{n}=\mathrm{0}\:,\mathrm{n}=\mathrm{1},\mathrm{n}=\mathrm{2}\:\mathrm{juste}\:\mathrm{evaluate} \\ $$$$\mathrm{for}\:\mathrm{n}\geqslant\mathrm{2} \\ $$$$\mathrm{p}\left(\mathrm{x}\right)=\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}} −\mathrm{nx}^{\mathrm{2}} −\mathrm{1} \\ $$$$\mathrm{p}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{p}'\left(\mathrm{x}\right)=\mathrm{2xn}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}−\mathrm{1}} −\mathrm{2nx} \\ $$$$\mathrm{p}'\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{p}''\left(\mathrm{x}\right)=\mathrm{2n}\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}−\mathrm{1}} +\mathrm{4x}^{\mathrm{2}} \mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}−\mathrm{2}} −\mathrm{2n} \\ $$$$\mathrm{p}''\left(\mathrm{0}\right)=\mathrm{2n}−\mathrm{2n}=\mathrm{0} \\ $$$$\mathrm{p}'''\left(\mathrm{x}\right)=\mathrm{4nx}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}−\mathrm{2}} +\mathrm{8xn}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}−\mathrm{2}} +\mathrm{8x}^{\mathrm{3}} \mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}−\mathrm{3}} \\ $$$$\mathrm{p}'''\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\mathrm{taylor}\:\mathrm{formula} \\ $$$$\mathrm{p}\left(\mathrm{x}\right)=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{2n}} {\sum}}\mathrm{p}^{\left(\mathrm{k}\right)} \left(\mathrm{0}\right).\frac{\mathrm{x}^{\mathrm{k}} }{\mathrm{k}!}=\frac{\mathrm{x}^{\mathrm{4}} \mathrm{p}^{\left(\mathrm{4}\right)} \left(\mathrm{0}\right)}{\mathrm{4}!}+.... \\ $$$$=\mathrm{x}^{\mathrm{4}} \left(.\mathrm{Q}\left(\mathrm{x}\right)\right) \\ $$$$\mathrm{Q}\left(\mathrm{x}\right)=\underset{\mathrm{k}=\mathrm{4}} {\overset{\mathrm{2n}} {\sum}}\frac{\mathrm{p}^{\left(\mathrm{k}\right)} \mathrm{x}^{\mathrm{k}−\mathrm{4}} }{\mathrm{k}!} \\ $$$$\Rightarrow\mathrm{X}^{\mathrm{4}} \mid\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}} −\mathrm{nx}^{\mathrm{2}} −\mathrm{1} \\ $$

Commented by mathmax by abdo last updated on 24/Oct/19

thanks sir.

$${thanks}\:{sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com