
Question and Answers Forum
Question Number 72046 by aliesam last updated on 23/Oct/19
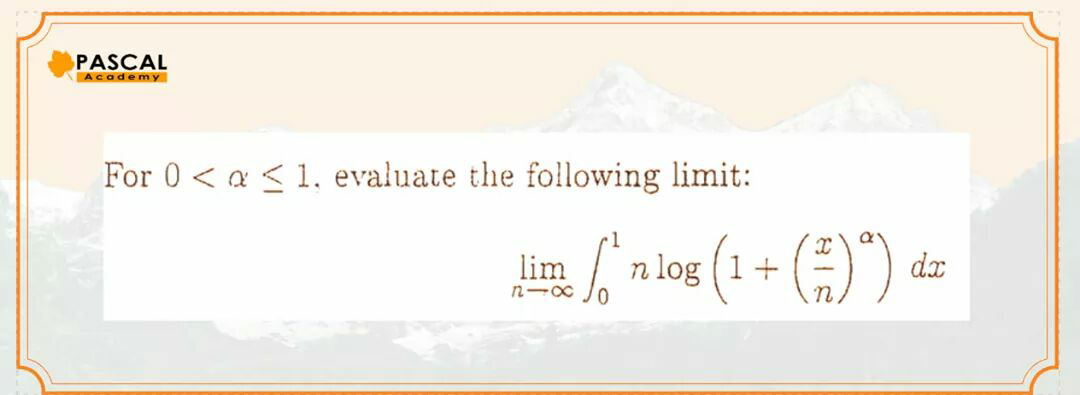
Commented by mathmax by abdo last updated on 26/Oct/19
![let U_n =∫_0 ^1 nln(1+((x/n))^α )dx ⇒U_n =_((x/n)=t) ∫_0 ^(1/n) nln(1+t^α )ndt =n^2 ∫_0 ^(1/n) ln(1+t^α )dt but 0<t<(1/n) and n→+∞ ln(1+t^α )∼t^α ⇒ U_n ∼n^2 ∫_0 ^(1/n) t^α dt =n^2 [(1/(α+1))t^(α+1) ]_0 ^(1/n) =(n^2 /(α+1))((1/n))^(α+1) =(1/((α+1)n^(α+1−2) )) =(1/((α+1)n^(α−1) )) =(n^(1−α) /((α+1))) →+∞ because 1−α>0 another way U_n =∫_R nln(1+((x/n))^α ) χ_([0,1]) (x)dx=∫_(R ) f_n (x)dx we have f_n (x)∼n((x/n))^α =((nx^n )/n^n ) =(x^α /n^(α−1) ) =n^(1−α) x^α but 1−α>0 ⇒ f_n (x)→+∞ (n→+∞) ⇒lim_(n→+∞) U_n =+∞](Q72263.png)
Commented by mathmax by abdo last updated on 26/Oct/19
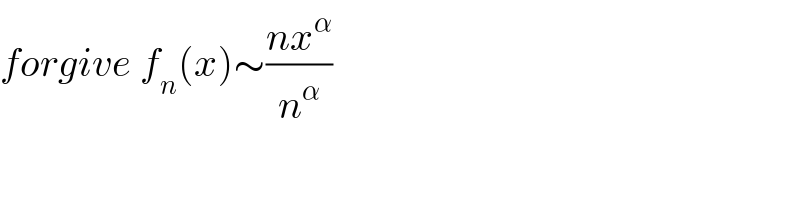
| ||
Question and Answers Forum | ||
Question Number 72046 by aliesam last updated on 23/Oct/19 | ||
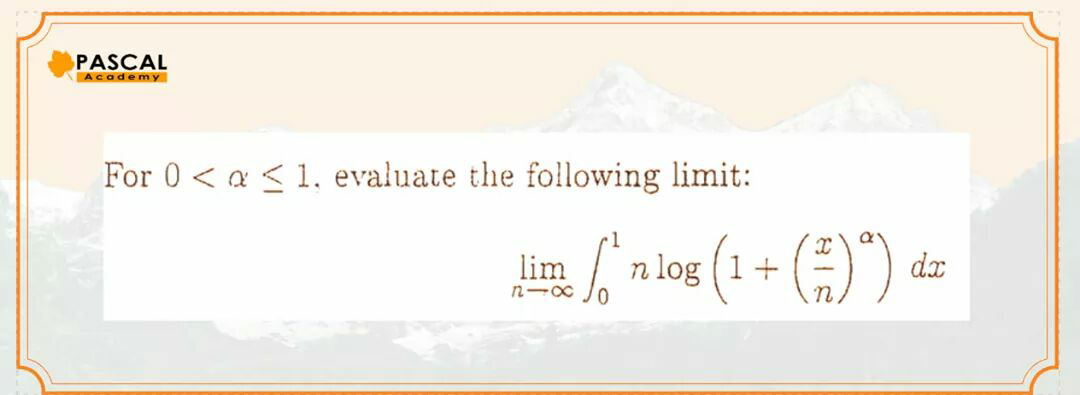 | ||
Commented by mathmax by abdo last updated on 26/Oct/19 | ||
![let U_n =∫_0 ^1 nln(1+((x/n))^α )dx ⇒U_n =_((x/n)=t) ∫_0 ^(1/n) nln(1+t^α )ndt =n^2 ∫_0 ^(1/n) ln(1+t^α )dt but 0<t<(1/n) and n→+∞ ln(1+t^α )∼t^α ⇒ U_n ∼n^2 ∫_0 ^(1/n) t^α dt =n^2 [(1/(α+1))t^(α+1) ]_0 ^(1/n) =(n^2 /(α+1))((1/n))^(α+1) =(1/((α+1)n^(α+1−2) )) =(1/((α+1)n^(α−1) )) =(n^(1−α) /((α+1))) →+∞ because 1−α>0 another way U_n =∫_R nln(1+((x/n))^α ) χ_([0,1]) (x)dx=∫_(R ) f_n (x)dx we have f_n (x)∼n((x/n))^α =((nx^n )/n^n ) =(x^α /n^(α−1) ) =n^(1−α) x^α but 1−α>0 ⇒ f_n (x)→+∞ (n→+∞) ⇒lim_(n→+∞) U_n =+∞](Q72263.png) | ||
Commented by mathmax by abdo last updated on 26/Oct/19 | ||
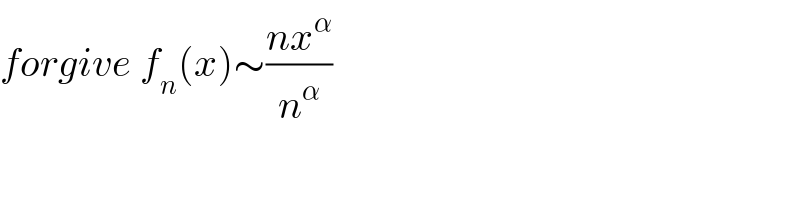 | ||