
Question Number 7207 by Tawakalitu. last updated on 16/Aug/16
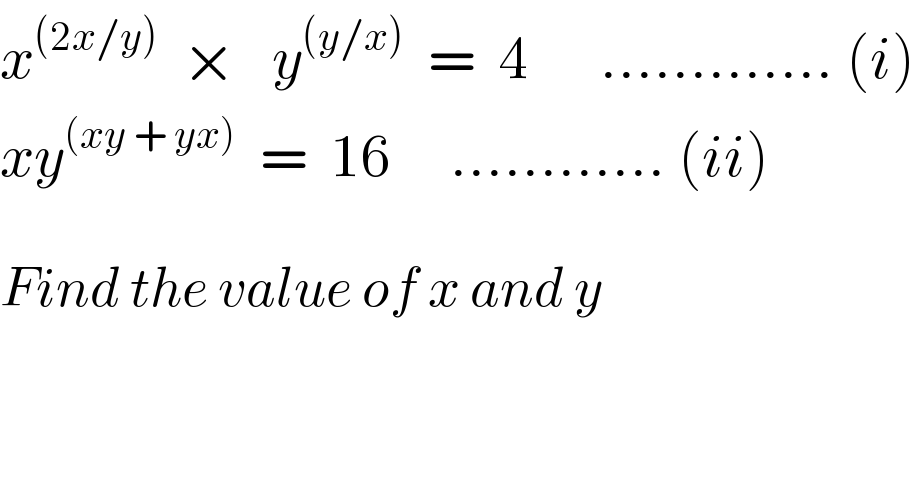
$${x}^{\left(\mathrm{2}{x}/{y}\right)} \:\:×\:\:\:{y}^{\left({y}/{x}\right)} \:\:=\:\:\mathrm{4}\:\:\:\:\:\:.............\:\left({i}\right) \\ $$$${xy}^{\left({xy}\:+\:{yx}\right)} \:\:=\:\:\mathrm{16}\:\:\:\:\:............\:\left({ii}\right) \\ $$$$ \\ $$$${Find}\:{the}\:{value}\:{of}\:{x}\:{and}\:{y} \\ $$
Commented by Yozzia last updated on 16/Aug/16
![ln{x^(2x/y) y^(y/x) }=ln4 ((2x)/y)lnx+(y/x)lny=ln4......(1) ln{xy^((xy+yx)) }=2ln4 lnx+(xy+yx)lny=2ln4 lnx+2xylny=2ln4............(2) Let u=lnx, v=lny⇒x=e^u , y=e^v ⇒(1): 2e^(u−v) u+e^(v−u) v=ln4 (2): u+2e^(u+v) v=2ln4 From (2): ve^v =(1/2){2ln4−u}e^(2ln4−u) ×e^(−2ln4) ve^v =(1/(32)){2ln4−u}e^(2ln4−u) 32ve^v ={ln16−u}e^(ln16−u) ⇒ln16−u=W(32ve^v ) u=ln16−W(32ve^v ) In (1): 2e^(2u) u+e^(2v) v=e^(u+v) ln4 2e^(2ln16−2W(32ve^v )) +ve^(2v) =e^(ln16−W(32ve^v )+v) ln4 2e^(ln256) e^(−2W(32ve^v )) +ve^(2v) =e^(ln16) e^(−W(32ve^v )) e^v ln4 512e^(−2W(32ve^v )) +ve^(2v) =(16ln4)e^v e^(−W(32ve^v )) ((512e^(−2v) {W(32ve^v )}^2 )/(1024v^2 ))+ve^(2v) =((16ln4)/(32v))×e^(−v) W(32ve^v ) (({W(32ve^v )}^2 )/(2v^2 ))+ve^(4v) =((ln4)/(2v))×e^v W(32ve^v ) {W(32ve^v )}^2 +2v^3 e^(4v) =ve^v W(32ve^v )ln4 {W(32ve^v )}^2 −2(ve^v ln2)W(32ve^v )+v^2 e^(2v) ln^2 2=v^2 e^(2v) ln^2 2−2v^3 e^(4v) [W(32ve^v )−ve^v ln2]^2 =v^2 e^(2v) (ln^2 2−2ve^(2v) ) ⇒W(32ve^v )−ve^v ln2=±ve^v (√(ln^2 2−2ve^(2v) )) W(32ve^v )=ve^v (ln2±(√(ln^2 2−2ve^(2v) )))](Q7208.png)
$${ln}\left\{{x}^{\mathrm{2}{x}/{y}} {y}^{{y}/{x}} \right\}={ln}\mathrm{4} \\ $$$$\frac{\mathrm{2}{x}}{{y}}{lnx}+\frac{{y}}{{x}}{lny}={ln}\mathrm{4}......\left(\mathrm{1}\right) \\ $$$${ln}\left\{{xy}^{\left({xy}+{yx}\right)} \right\}=\mathrm{2}{ln}\mathrm{4} \\ $$$${lnx}+\left({xy}+{yx}\right){lny}=\mathrm{2}{ln}\mathrm{4} \\ $$$${lnx}+\mathrm{2}{xylny}=\mathrm{2}{ln}\mathrm{4}............\left(\mathrm{2}\right) \\ $$$${Let}\:{u}={lnx},\:{v}={lny}\Rightarrow{x}={e}^{{u}} ,\:{y}={e}^{{v}} \\ $$$$\Rightarrow\left(\mathrm{1}\right):\:\mathrm{2}{e}^{{u}−{v}} {u}+{e}^{{v}−{u}} {v}={ln}\mathrm{4} \\ $$$$\left(\mathrm{2}\right):\:{u}+\mathrm{2}{e}^{{u}+{v}} {v}=\mathrm{2}{ln}\mathrm{4} \\ $$$${From}\:\left(\mathrm{2}\right):\:{ve}^{{v}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{2}{ln}\mathrm{4}−{u}\right\}{e}^{\mathrm{2}{ln}\mathrm{4}−{u}} ×{e}^{−\mathrm{2}{ln}\mathrm{4}} \\ $$$${ve}^{{v}} =\frac{\mathrm{1}}{\mathrm{32}}\left\{\mathrm{2}{ln}\mathrm{4}−{u}\right\}{e}^{\mathrm{2}{ln}\mathrm{4}−{u}} \\ $$$$\mathrm{32}{ve}^{{v}} =\left\{{ln}\mathrm{16}−{u}\right\}{e}^{{ln}\mathrm{16}−{u}} \\ $$$$\Rightarrow{ln}\mathrm{16}−{u}={W}\left(\mathrm{32}{ve}^{{v}} \right) \\ $$$${u}={ln}\mathrm{16}−{W}\left(\mathrm{32}{ve}^{{v}} \right) \\ $$$${In}\:\left(\mathrm{1}\right):\:\mathrm{2}{e}^{\mathrm{2}{u}} {u}+{e}^{\mathrm{2}{v}} {v}={e}^{{u}+{v}} {ln}\mathrm{4} \\ $$$$\mathrm{2}{e}^{\mathrm{2}{ln}\mathrm{16}−\mathrm{2}{W}\left(\mathrm{32}{ve}^{{v}} \right)} +{ve}^{\mathrm{2}{v}} ={e}^{{ln}\mathrm{16}−{W}\left(\mathrm{32}{ve}^{{v}} \right)+{v}} {ln}\mathrm{4} \\ $$$$\mathrm{2}{e}^{{ln}\mathrm{256}} {e}^{−\mathrm{2}{W}\left(\mathrm{32}{ve}^{{v}} \right)} +{ve}^{\mathrm{2}{v}} ={e}^{{ln}\mathrm{16}} {e}^{−{W}\left(\mathrm{32}{ve}^{{v}} \right)} {e}^{{v}} {ln}\mathrm{4} \\ $$$$\mathrm{512}{e}^{−\mathrm{2}{W}\left(\mathrm{32}{ve}^{{v}} \right)} +{ve}^{\mathrm{2}{v}} =\left(\mathrm{16}{ln}\mathrm{4}\right){e}^{{v}} {e}^{−{W}\left(\mathrm{32}{ve}^{{v}} \right)} \\ $$$$\frac{\mathrm{512}{e}^{−\mathrm{2}{v}} \left\{{W}\left(\mathrm{32}{ve}^{{v}} \right)\right\}^{\mathrm{2}} }{\mathrm{1024}{v}^{\mathrm{2}} }+{ve}^{\mathrm{2}{v}} =\frac{\mathrm{16}{ln}\mathrm{4}}{\mathrm{32}{v}}×{e}^{−{v}} {W}\left(\mathrm{32}{ve}^{{v}} \right) \\ $$$$\frac{\left\{{W}\left(\mathrm{32}{ve}^{{v}} \right)\right\}^{\mathrm{2}} }{\mathrm{2}{v}^{\mathrm{2}} }+{ve}^{\mathrm{4}{v}} =\frac{{ln}\mathrm{4}}{\mathrm{2}{v}}×{e}^{{v}} {W}\left(\mathrm{32}{ve}^{{v}} \right) \\ $$$$\left\{{W}\left(\mathrm{32}{ve}^{{v}} \right)\right\}^{\mathrm{2}} +\mathrm{2}{v}^{\mathrm{3}} {e}^{\mathrm{4}{v}} ={ve}^{{v}} {W}\left(\mathrm{32}{ve}^{{v}} \right){ln}\mathrm{4} \\ $$$$\left\{{W}\left(\mathrm{32}{ve}^{{v}} \right)\right\}^{\mathrm{2}} −\mathrm{2}\left({ve}^{{v}} {ln}\mathrm{2}\right){W}\left(\mathrm{32}{ve}^{{v}} \right)+{v}^{\mathrm{2}} {e}^{\mathrm{2}{v}} {ln}^{\mathrm{2}} \mathrm{2}={v}^{\mathrm{2}} {e}^{\mathrm{2}{v}} {ln}^{\mathrm{2}} \mathrm{2}−\mathrm{2}{v}^{\mathrm{3}} {e}^{\mathrm{4}{v}} \\ $$$$\left[{W}\left(\mathrm{32}{ve}^{{v}} \right)−{ve}^{{v}} {ln}\mathrm{2}\right]^{\mathrm{2}} ={v}^{\mathrm{2}} {e}^{\mathrm{2}{v}} \left({ln}^{\mathrm{2}} \mathrm{2}−\mathrm{2}{ve}^{\mathrm{2}{v}} \right) \\ $$$$\Rightarrow{W}\left(\mathrm{32}{ve}^{{v}} \right)−{ve}^{{v}} {ln}\mathrm{2}=\pm{ve}^{{v}} \sqrt{{ln}^{\mathrm{2}} \mathrm{2}−\mathrm{2}{ve}^{\mathrm{2}{v}} } \\ $$$${W}\left(\mathrm{32}{ve}^{{v}} \right)={ve}^{{v}} \left({ln}\mathrm{2}\pm\sqrt{{ln}^{\mathrm{2}} \mathrm{2}−\mathrm{2}{ve}^{\mathrm{2}{v}} }\right) \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 16/Aug/16
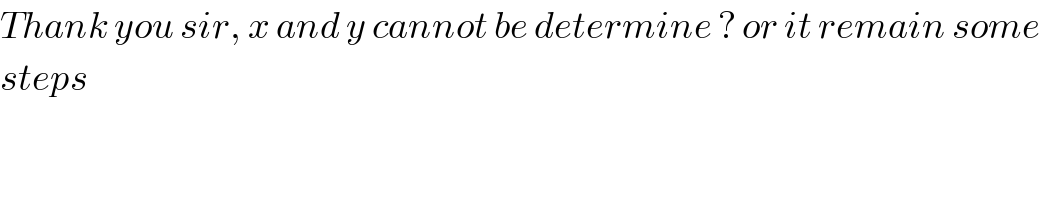
$${Thank}\:{you}\:{sir},\:{x}\:{and}\:{y}\:{cannot}\:{be}\:{determine}\:?\:{or}\:{it}\:{remain}\:{some} \\ $$$${steps} \\ $$
Commented by Yozzia last updated on 16/Aug/16
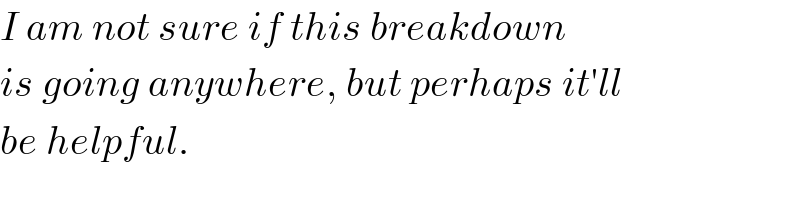
$${I}\:{am}\:{not}\:{sure}\:{if}\:{this}\:{breakdown} \\ $$$${is}\:{going}\:{anywhere},\:{but}\:{perhaps}\:{it}'{ll} \\ $$$${be}\:{helpful}. \\ $$
Commented by Tawakalitu. last updated on 16/Aug/16

$${Thank}\:{you}\:{sir} \\ $$
