Question and Answers Forum
Question Number 72408 by ajfour last updated on 28/Oct/19
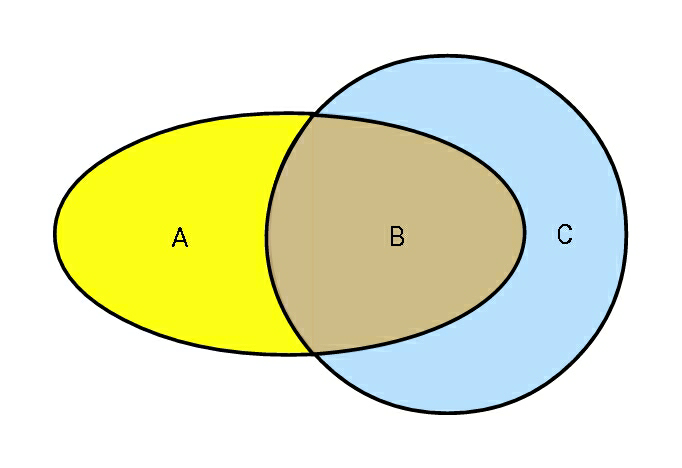
Commented by ajfour last updated on 28/Oct/19

Answered by mr W last updated on 28/Oct/19
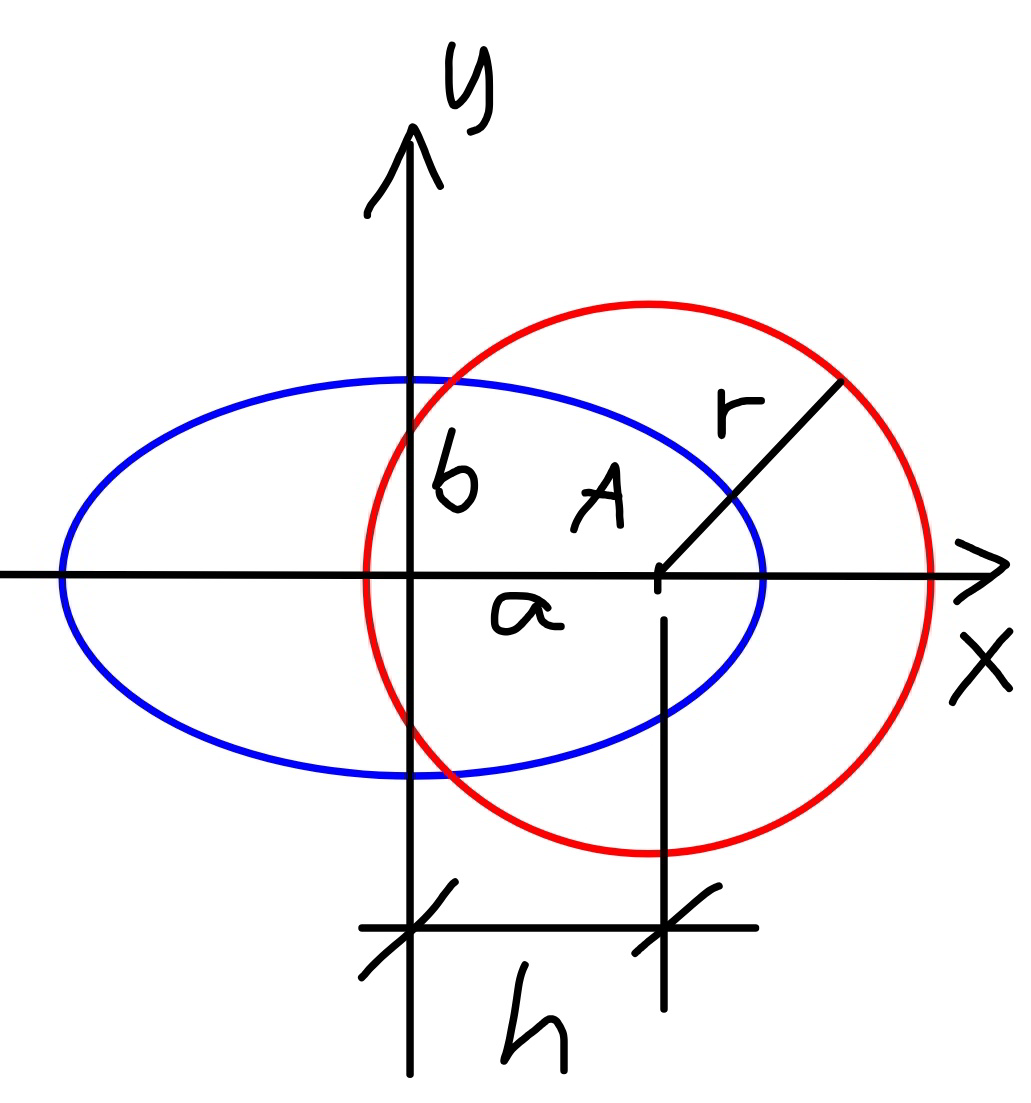
Commented by mr W last updated on 29/Oct/19
![eqn. of circle: (x−h)^2 +y^2 =r^2 eqn. of ellipse: (x^2 /a^2 )+(y^2 /b^2 )=1 (x^2 /a^2 )+((r^2 −(x−h)^2 )/b^2 )=1 b^2 x^2 +a^2 r^2 −a^2 (x^2 −2hx+h^2 )=a^2 b^2 (a^2 −b^2 )x^2 −2a^2 hx+a^2 (b^2 +h^2 −r^2 )=0 x=((a^2 h−a(√(a^2 h^2 −(a^2 −b^2 )(b^2 +h^2 −r^2 ))))/(a^2 −b^2 )) x=((a^2 h−a(√((a^2 −b^2 )(r^2 −b^2 )+h^2 b^2 )))/(a^2 −b^2 ))=k area of circle=area of ellipse πr^2 =πab ⇒r^2 =ab with λ=(b/a), η=(h/a) (k/a)=κ=((η−(√(λ(1−λ)(1−λ^2 )+λ^2 η^2 )))/(1−λ^2 )) 2∫_(h−r) ^k (√(r^2 −(x−h)^2 ))dx+2∫_k ^a b(√(1−(x^2 /a^2 )))dx=((πab)/2) ∫_(h−(√λ)a) ^k (√(λ−((x/a)−(h/a))^2 ))d((x/a))+λ∫_k ^a (√(1−(x^2 /a^2 )))d((x/a))=((πλ)/4) ∫_(η−(√λ)) ^κ (√(λ−(ξ−η)^2 ))dξ+λ∫_κ ^1 (√(1−ξ^2 ))dξ=((πλ)/4) (1/2)[λ sin^(−1) ((ξ−η)/(√λ))+(ξ−η)(√(λ−(ξ−η)^2 ))]_(η−(√λ)) ^κ +(λ/2)[sin^(−1) ξ+ξ(√(1−ξ^2 ))]_κ ^1 =((πλ)/4) ⇒ sin^(−1) ((κ−η)/(√λ))+((κ−η)/(√λ))(√(1−(((κ−η)/(√λ)))^2 ))+(π/2)=sin^(−1) κ+κ(√(1−κ^2 )) this is an eqn. for η in terms of λ. examples: λ=0.5 ⇒ η=0.6432 λ=0.75 ⇒ η=0.7441 λ=2 ⇒ η=0.9096](Q72423.png)
Commented by ajfour last updated on 28/Oct/19
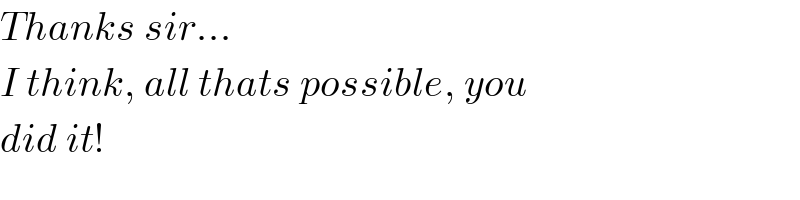
Commented by mr W last updated on 28/Oct/19
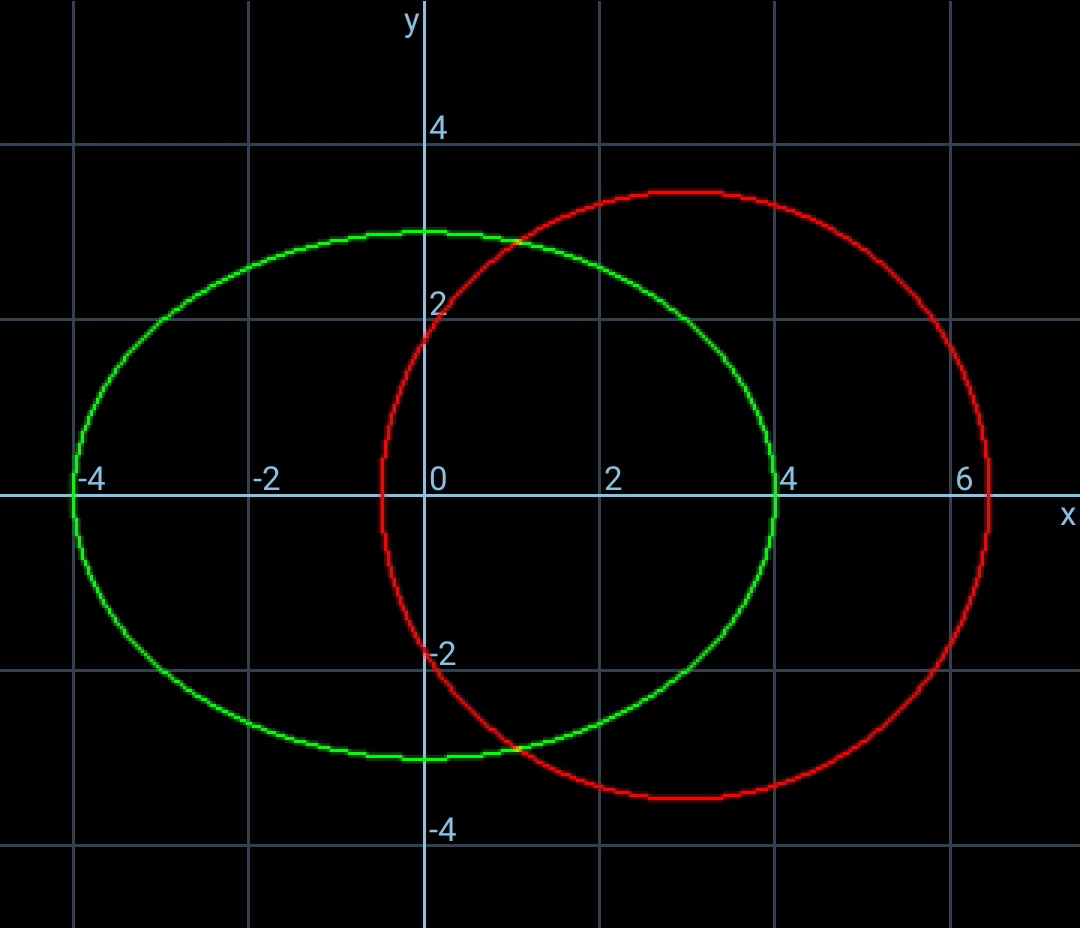
Commented by mr W last updated on 29/Oct/19
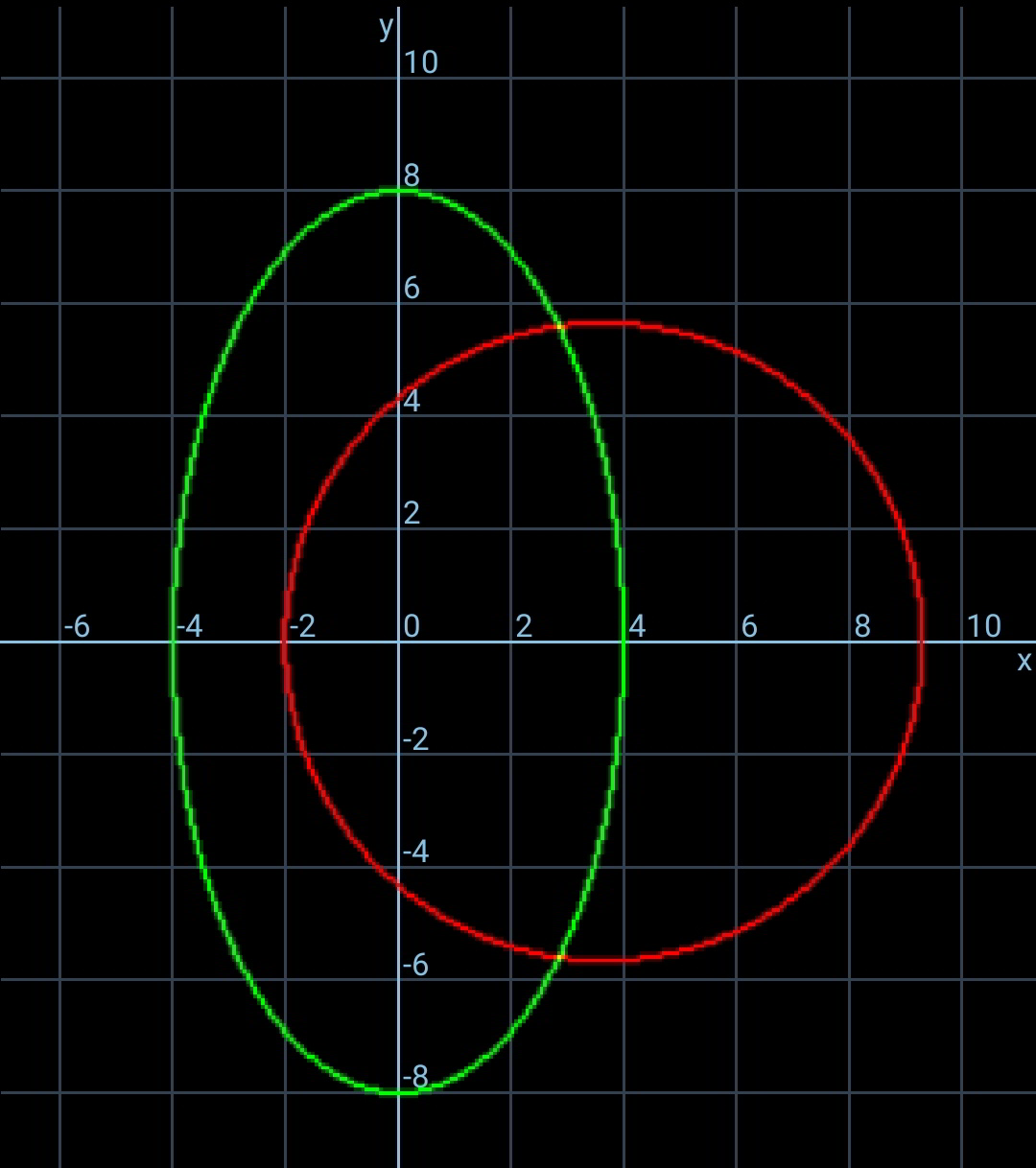
Commented by ajfour last updated on 29/Oct/19
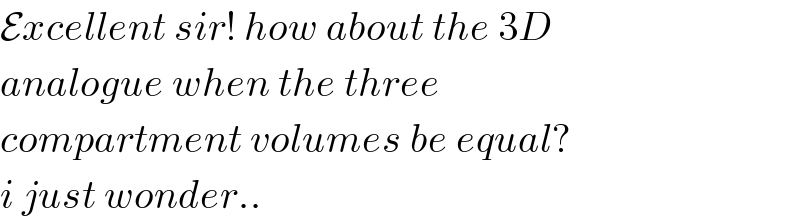
Commented by ajfour last updated on 29/Oct/19