
Question and Answers Forum
Question Number 72488 by aliesam last updated on 29/Oct/19
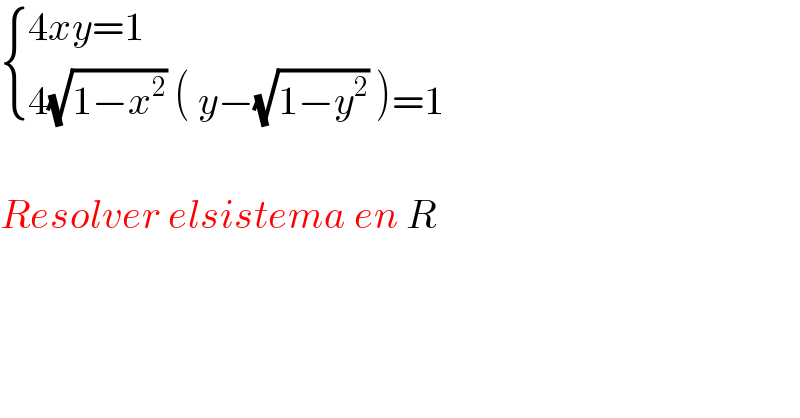
Answered by behi83417@gmail.com last updated on 30/Oct/19
![x=cost,y=cosr ⇒ { ((4sint(cosr−sinr)=1)),((4cost.cosr=1)) :} ⇒(1/((cosr−sinr)^2 ))+(1/(cos^2 r))=4⇒ ⇒cos^2 r+(cosr−sinr)^2 =4cos^2 r.(cosr−sinr)^2 ((1+cos2r)/2)+1−sin2r=2(1+cos2r)(1−sin2r) ⇒1+cos2r+2−2sin2r= 4(1−sin2r+cos2r−sin2rcos2r) ⇒3+cos2r−2sin2r= 4−4sin2r+4cos2r−4sin2rcos2r ⇒3cos2r−2sin2r−4sin2rcos2r+1=0 [let:c=cos2r,s=sin2r]⇒ 3c−2s−4sc+1=0 9c^2 +4s^2 −12sc=16s^2 c^2 −8sc+1 9c^2 +4s^2 −16s^2 c^2 =4sc+1 5c^2 −16c^2 (1−c^2 )+3=4sc ⇒16c^4 −11c^2 +3=4sc ⇒256c^8 +121c^4 +9−352c^6 +96c^4 −66c^2 = =16c^2 −16c^4 ⇒256c^8 −352c^6 +233c^4 −82c^2 +9=0 ⇒c=±0.42,±0.76 ⇒cos2r=±0.42,±0.76 ⇒ { ((cos2r=0.42⇒y=cosr=0.843)),((⇒x=(1/(4y))=(1/(4×0.843))=0.211)) :} ⇒ { ((cos2r=−0.42⇒y=cosr=0.54)),((x=(1/(4y))=(1/(4×0.211))=0.053)) :} ⇒ { ((cos2r=0.76⇒y=cosr=0.938)),((x=(1/(4y))=(1/(4×0.938))=0.235)) :} ⇒ { ((cos2r=−0.76⇒y=cosr=0.346)),((x=(1/(4y))=(1/(4×0.346))=0.087)) :}](Q72510.png)
Commented by aliesam last updated on 29/Oct/19

Answered by MJS last updated on 29/Oct/19

| ||
Question and Answers Forum | ||
Question Number 72488 by aliesam last updated on 29/Oct/19 | ||
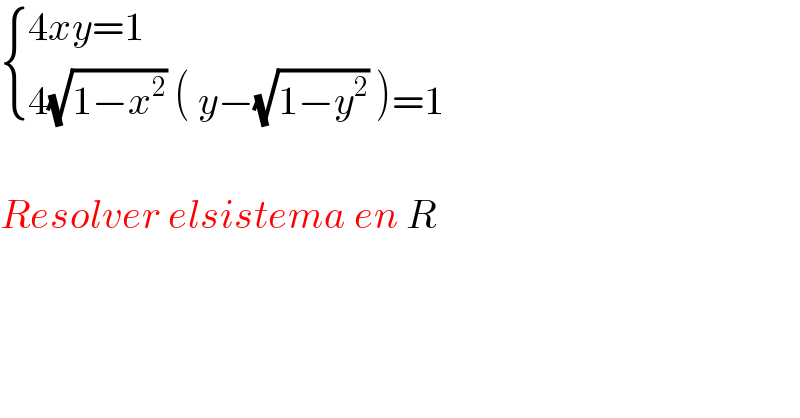 | ||
Answered by behi83417@gmail.com last updated on 30/Oct/19 | ||
![x=cost,y=cosr ⇒ { ((4sint(cosr−sinr)=1)),((4cost.cosr=1)) :} ⇒(1/((cosr−sinr)^2 ))+(1/(cos^2 r))=4⇒ ⇒cos^2 r+(cosr−sinr)^2 =4cos^2 r.(cosr−sinr)^2 ((1+cos2r)/2)+1−sin2r=2(1+cos2r)(1−sin2r) ⇒1+cos2r+2−2sin2r= 4(1−sin2r+cos2r−sin2rcos2r) ⇒3+cos2r−2sin2r= 4−4sin2r+4cos2r−4sin2rcos2r ⇒3cos2r−2sin2r−4sin2rcos2r+1=0 [let:c=cos2r,s=sin2r]⇒ 3c−2s−4sc+1=0 9c^2 +4s^2 −12sc=16s^2 c^2 −8sc+1 9c^2 +4s^2 −16s^2 c^2 =4sc+1 5c^2 −16c^2 (1−c^2 )+3=4sc ⇒16c^4 −11c^2 +3=4sc ⇒256c^8 +121c^4 +9−352c^6 +96c^4 −66c^2 = =16c^2 −16c^4 ⇒256c^8 −352c^6 +233c^4 −82c^2 +9=0 ⇒c=±0.42,±0.76 ⇒cos2r=±0.42,±0.76 ⇒ { ((cos2r=0.42⇒y=cosr=0.843)),((⇒x=(1/(4y))=(1/(4×0.843))=0.211)) :} ⇒ { ((cos2r=−0.42⇒y=cosr=0.54)),((x=(1/(4y))=(1/(4×0.211))=0.053)) :} ⇒ { ((cos2r=0.76⇒y=cosr=0.938)),((x=(1/(4y))=(1/(4×0.938))=0.235)) :} ⇒ { ((cos2r=−0.76⇒y=cosr=0.346)),((x=(1/(4y))=(1/(4×0.346))=0.087)) :}](Q72510.png) | ||
| ||
Commented by aliesam last updated on 29/Oct/19 | ||
 | ||
Answered by MJS last updated on 29/Oct/19 | ||
 | ||
| ||