Question Number 7249 by Rasheed Soomro last updated on 19/Aug/16
$${w},{x},{y},{z}\:{are}\:{digits}\:{in}\:{respective}\:{base}\:{system}\:{and} \\ $$$${a},{b}\:{are}\:{bases}. \\ $$$${Find}\:{out}\:{an}\:{example}/{examples}\:{which}\:{satisfy} \\ $$$${the}\:{following} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{wxyz}_{{a}} +{wxyz}_{{b}} ={wxyz}_{{a}+{b}} \: \\ $$
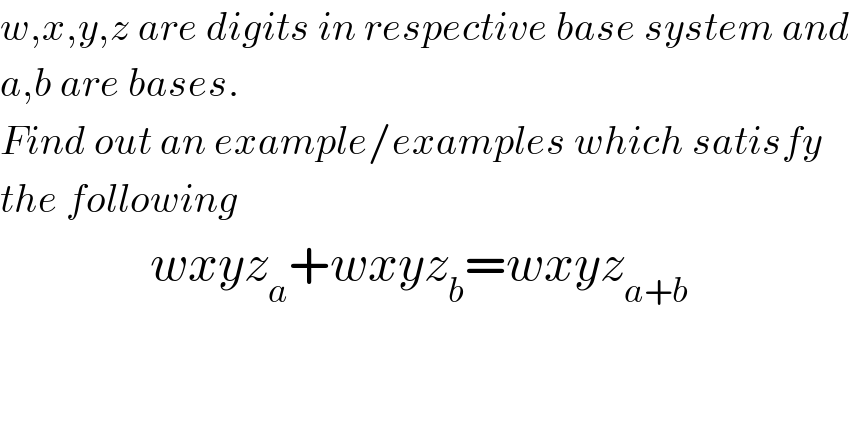
Commented by Yozzia last updated on 19/Aug/16
$$\mathrm{2}^{\mathrm{1}} +\mathrm{2}^{\mathrm{1}} =\left(\mathrm{2}+\mathrm{2}\right)^{\mathrm{1}} =\mathrm{4}^{\mathrm{1}} \\ $$$$\left\{\mathrm{1}×\mathrm{2}+\mathrm{0}×\mathrm{2}^{\mathrm{0}} \right\}+\left\{\mathrm{1}×\mathrm{2}+\mathrm{0}×\mathrm{2}^{\mathrm{0}} \right\}=\mathrm{1}×\mathrm{4}+\mathrm{0}×\mathrm{4}^{\mathrm{0}} \\ $$$${or}\:\left(\mathrm{10}\right)_{\mathrm{2}} +\left(\mathrm{10}\right)_{\mathrm{2}} =\left(\mathrm{10}\right)_{\mathrm{4}} \\ $$
Commented by Rasheed Soomro last updated on 19/Aug/16
$${Four}\:{digit}\:{number}\:{is}\:{required}. \\ $$
Commented by Yozzia last updated on 19/Aug/16
![wxyz_a +wxyz_b =wxyz_(a+b) (∗) Suppose wxyz is an integer identical on both sides of (∗) e.g 1234_a +1234_b =1234_(a+b) for some given a,b∈N. [wa^3 +xa^2 +ya+z]+[wb^3 +xb^2 +yb+z]=w(a+b)^3 +x(a+b)^2 +y(a+b)+z w{a^3 +b^3 −(a+b)^3 }+x{a^2 +b^2 −(a+b)^2 }+y(a+b−a−b)+2z−z=0 w{−3a^2 b−3ab^2 }+x{−2ab}+z=0 w{3a^2 b+3ab^2 }+2xab−z=0 The form of the above equation is independent of the value of y∈N. z=ab(2x+3w(a+b)) w,x∈Z^≥ , a,b∈N−{1} and ab∣z. If x>0 or w>0 then 2x+3w(a+b)>1⇒z>ab>a and z>b. However, 0≤z≤min(a−1,b−1)<min(a,b) for z in wxyz_a and wxyz_b , a contradiction. Hence, we must have x=w=0 ⇒ z=0. ∴ we get 00y0_a +00y0_b =00y0_(a+b) or y0_a +y0_b =y0_(a+b) or ya+yb=y(a+b) for any y∈N ,0≤y<a,y<b when a and b are known bases. No four digit integer wxyz satisfies wxyz_a +wxyz_b =wxyz_(a+b) .](Q7257.png)
$${wxyz}_{{a}} +{wxyz}_{{b}} ={wxyz}_{{a}+{b}} \:\:\:\:\left(\ast\right) \\ $$$${Suppose}\:{wxyz}\:{is}\:{an}\:{integer}\:{identical}\:{on}\:{both}\:{sides}\:{of}\:\left(\ast\right) \\ $$$${e}.{g}\:\:\mathrm{1234}_{{a}} +\mathrm{1234}_{{b}} =\mathrm{1234}_{{a}+{b}} \: \\ $$$${for}\:{some}\:{given}\:{a},{b}\in\mathbb{N}. \\ $$$$\left[{wa}^{\mathrm{3}} +{xa}^{\mathrm{2}} +{ya}+{z}\right]+\left[{wb}^{\mathrm{3}} +{xb}^{\mathrm{2}} +{yb}+{z}\right]={w}\left({a}+{b}\right)^{\mathrm{3}} +{x}\left({a}+{b}\right)^{\mathrm{2}} +{y}\left({a}+{b}\right)+{z} \\ $$$${w}\left\{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} −\left({a}+{b}\right)^{\mathrm{3}} \right\}+{x}\left\{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\left({a}+{b}\right)^{\mathrm{2}} \right\}+{y}\left({a}+{b}−{a}−{b}\right)+\mathrm{2}{z}−{z}=\mathrm{0} \\ $$$${w}\left\{−\mathrm{3}{a}^{\mathrm{2}} {b}−\mathrm{3}{ab}^{\mathrm{2}} \right\}+{x}\left\{−\mathrm{2}{ab}\right\}+{z}=\mathrm{0} \\ $$$${w}\left\{\mathrm{3}{a}^{\mathrm{2}} {b}+\mathrm{3}{ab}^{\mathrm{2}} \right\}+\mathrm{2}{xab}−{z}=\mathrm{0}\:\: \\ $$$${The}\:{form}\:{of}\:{the}\:{above}\:{equation}\:{is}\: \\ $$$${independent}\:{of}\:{the}\:{value}\:{of}\:{y}\in\mathbb{N}. \\ $$$${z}={ab}\left(\mathrm{2}{x}+\mathrm{3}{w}\left({a}+{b}\right)\right) \\ $$$${w},{x}\in\mathbb{Z}^{\geqslant} ,\:{a},{b}\in\mathbb{N}−\left\{\mathrm{1}\right\}\:{and}\:{ab}\mid{z}.\:{If}\:{x}>\mathrm{0}\:{or}\:{w}>\mathrm{0} \\ $$$${then}\:\mathrm{2}{x}+\mathrm{3}{w}\left({a}+{b}\right)>\mathrm{1}\Rightarrow{z}>{ab}>{a}\:{and}\:{z}>{b}. \\ $$$${However},\:\mathrm{0}\leqslant{z}\leqslant{min}\left({a}−\mathrm{1},{b}−\mathrm{1}\right)<{min}\left({a},{b}\right) \\ $$$${for}\:{z}\:{in}\:{wxyz}_{{a}} \:{and}\:{wxyz}_{{b}} ,\:{a}\:{contradiction}. \\ $$$${Hence},\:{we}\:{must}\:{have}\:{x}={w}=\mathrm{0}\:\Rightarrow\:{z}=\mathrm{0}. \\ $$$$\therefore\:{we}\:{get}\:\mathrm{00}{y}\mathrm{0}_{{a}} +\mathrm{00}{y}\mathrm{0}_{{b}} =\mathrm{00}{y}\mathrm{0}_{{a}+{b}} \:\:{or}\:{y}\mathrm{0}_{{a}} +{y}\mathrm{0}_{{b}} ={y}\mathrm{0}_{{a}+{b}} \\ $$$${or}\:{ya}+{yb}={y}\left({a}+{b}\right)\:{for}\:{any}\:{y}\in\mathbb{N}\:,\mathrm{0}\leqslant{y}<{a},{y}<{b} \\ $$$${when}\:{a}\:{and}\:{b}\:{are}\:{known}\:{bases}. \\ $$$${No}\:{four}\:{digit}\:{integer}\:{wxyz}\:{satisfies} \\ $$$${wxyz}_{{a}} +{wxyz}_{{b}} ={wxyz}_{{a}+{b}} . \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 20/Aug/16
$$\mathcal{V}.\:\mathcal{N}{ic}\mathcal{E}! \\ $$$${What}\:{is}\:{meant}\:{by}\::\:\:\:\:\:{w},{x}\in\mathbb{Z}^{\geqslant} \:\:\:? \\ $$
Commented by Yozzia last updated on 20/Aug/16
$$\mathbb{Z}^{\geqslant} =\left\{\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},...\right\} \\ $$$${w},{x}\in\mathbb{Z}^{\geqslant} \equiv{x},{w}\:{are}\:{non}−{negative}\:{integers}. \\ $$
Commented by Rasheed Soomro last updated on 20/Aug/16
$$\mathcal{T}{h}\alpha{nk}\mathcal{S}! \\ $$
Commented by Yozzia last updated on 20/Aug/16
![Let q be a number of digit length n≥3, and c,b∈[N−{1}]. Write k_m for the number k corresponding to base m≥2. Suppose that q_c +q_b =q_(c+b) . Then, no q exists satisfying this equation for n≥3. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− PROOF: Looking at the equation q_c +q_b =q_(c+b) , q has a digit representation of the form q=a_0 ^ a_1 ^ a_2 ^ a_3 ^ ...a_(n−1) ^ where 0≤a_i ≤min(c−1,b−1) for i=1 , 2 , ... , n−1, and 1≤a_0 ≤min(c−1,b−1). Therefore q_c =Σ_(i=0) ^(n−1) a_i c^(n−1−i) , q_b =Σ_(i=1) ^(n−1) a_i b^(n−1−i) and q_(c+b) =Σ_(i=0) ^(n−1) a_i (b+c)^(n−1−i) . Σ_(i=0) ^(n−1) a_i c^(n−1−i) +Σ_(i=0) ^(n−1) a_i b^(n−1−i) =Σ_(i=0) ^(n−1) a_i (b+c)^(n−1−i) Σ_(i=0) ^(n−1) {a_i c^(n−1−i) +a_i b^(n−1−i) −a_i (b+c)^(n−1−i) }=0 Σ_(i=0) ^(n−1) [a_i {c^(n−1−i) +b^(n−1−i) −(b+c)^(n−1−i) }]=0 Σ_(i=0) ^(n−3) [a_i {c^(n−1−i) +b^(n−1−i) −(b+c)^(n−1−i) }]+a_(n−2) {c^(n−1−n+2) +b^(n−1−n+2) −(b+c)^(n−1−n+2) }+a_(n−1) {c^(n−1−n+1) +b^(n−1−n+1) −(b+c)^(n−1−n+1) }=0 Σ_(i=0) ^(n−3) [a_i {c^(n−1−i) +b^(n−1−i) −(b+c)^(n−1−i) }]+a_(n−2) {c+b−(b+c)}+a_(n−1) {1+1−1}=0 Σ_(i=0) ^(n−3) [a_i {c^(n−1−i) +b^(n−1−i) −(b+c)^(n−1−i) }]+a_(n−1) =0 a_(n−1) =Σ_(i=0) ^(n−3) [a_i {(b+c)^(n−1−i) −c^(n−1−i) −b^(n−1−i) }] According to the Binomial Theorem, (b+c)^(n−1−i) =Σ_(k=0) ^(n−1−i) (((n−1−i)),(k) ) b^(n−1−i−k) c^k or (b+c)^(n−1−i) =b^(n−1−i) +c^(n−1−i) +Σ_(k=1) ^(n−2−i) (((n−1−i)),(k) ) b^(n−1−i−k) c^k . ∴ (b+c)^(n−1−i) −b^(n−1−i) −c^(n−1−i) =Σ_(k=1) ^(n−2−i) (((n−1−i)),(k) ) b^(n−1−i−k) c^k . a_(n−1) =Σ_(i=0) ^(n−3) [a_i {Σ_(k=1) ^(n−2−i) (((n−1−i)),(k) ) b^(n−1−i−k) c^k }] a_(n−1) =a_0 {Σ_(k=1) ^(n−2) (((n−1)),(k) ) b^(n−1−k) c^k }+a_1 {Σ_(k=1) ^(n−3) (((n−2)),(k) ) b^(n−2−k) c^k } +a_2 {Σ_(k=1) ^(n−4) (((n−3)),(k) ) b^(n−3−k) c^k }+...+a_(n−4) {Σ_(k=1) ^2 ((3),(k) ) b^(3−k) c^k }+a_(n−3) {Σ_(k=1) ^1 ((2),(k) ) b^(2−k) c^k } Observe that the form of the above equation is indepedent of a_(n−2) ; so a_(n−2) is a free variable such that 0≤a_(n−2) ≤min(c−1,b−1). −−−−−−−−−−−−−−−−−−−−−−−−−−−−− Proposition: For any n≥3, bc divides Σ_(k=1) ^(n−2) (((n−1)),(k) ) b^(n−1−k) c^k . Proof (induction): Base case n=3: Σ_(k=1) ^(3−2) (((3−1)),(k) ) b^(3−1−k) c^k = ((2),(1) ) bc ⇒bc divides Σ_(k=1) ^(n−2) (((n−1)),(k) ) b^(n−1−k) c^k for n=3. Inductive step: Suppose bc divides Σ_(k=1) ^(j−2) (((j−1)),(k) ) b^(j−1−k) c^k for n=j. i.e Σ_(k=1) ^(j−2) (((j−1)),(k) ) b^(j−1−k) c^k =rbc for some r∈N. For n=j+1, we have that Σ_(k=1) ^(j−1) ((j),(k) ) b^(j−k) c^k =Σ_(k=1) ^(j−1) { (((j−1)),(k) ) + (((j−1)),((k−1)) )}b^(j−k) c^k](Q7277.png)
$${Let}\:{q}\:{be}\:{a}\:{number}\:{of}\:{digit}\:{length}\:{n}\geqslant\mathrm{3}, \\ $$$${and}\:{c},{b}\in\left[\mathbb{N}−\left\{\mathrm{1}\right\}\right].\:{Write}\:{k}_{{m}} \:{for}\:{the} \\ $$$${number}\:{k}\:{corresponding}\:{to}\:{base}\:{m}\geqslant\mathrm{2}. \\ $$$${Suppose}\:{that}\:{q}_{{c}} +{q}_{{b}} ={q}_{{c}+{b}} .\: \\ $$$${Then},\:{no}\:{q}\:{exists}\:{satisfying}\:{this}\:{equation} \\ $$$${for}\:{n}\geqslant\mathrm{3}. \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${PROOF}: \\ $$$${Looking}\:{at}\:{the}\:{equation}\:{q}_{{c}} +{q}_{{b}} ={q}_{{c}+{b}} , \\ $$$${q}\:{has}\:{a}\:{digit}\:{representation}\:{of}\:{the}\:{form} \\ $$$${q}=\bar {{a}}_{\mathrm{0}} \bar {{a}}_{\mathrm{1}} \bar {{a}}_{\mathrm{2}} \bar {{a}}_{\mathrm{3}} ...\bar {{a}}_{{n}−\mathrm{1}} \:{where}\:\mathrm{0}\leqslant{a}_{{i}} \leqslant{min}\left({c}−\mathrm{1},{b}−\mathrm{1}\right) \\ $$$${for}\:{i}=\mathrm{1}\:,\:\mathrm{2}\:,\:...\:,\:{n}−\mathrm{1},\:{and}\:\mathrm{1}\leqslant{a}_{\mathrm{0}} \leqslant{min}\left({c}−\mathrm{1},{b}−\mathrm{1}\right). \\ $$$${Therefore}\:{q}_{{c}} =\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{a}_{{i}} {c}^{{n}−\mathrm{1}−{i}} \:,\:{q}_{{b}} =\underset{{i}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}{a}_{{i}} {b}^{{n}−\mathrm{1}−{i}} \\ $$$${and}\:{q}_{{c}+{b}} =\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{a}_{{i}} \left({b}+{c}\right)^{{n}−\mathrm{1}−{i}} .\: \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{a}_{{i}} {c}^{{n}−\mathrm{1}−{i}} +\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{a}_{{i}} {b}^{{n}−\mathrm{1}−{i}} =\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{a}_{{i}} \left({b}+{c}\right)^{{n}−\mathrm{1}−{i}} \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\left\{{a}_{{i}} {c}^{{n}−\mathrm{1}−{i}} +{a}_{{i}} {b}^{{n}−\mathrm{1}−{i}} −{a}_{{i}} \left({b}+{c}\right)^{{n}−\mathrm{1}−{i}} \right\}=\mathrm{0} \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\left[{a}_{{i}} \left\{{c}^{{n}−\mathrm{1}−{i}} +{b}^{{n}−\mathrm{1}−{i}} −\left({b}+{c}\right)^{{n}−\mathrm{1}−{i}} \right\}\right]=\mathrm{0} \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{3}} {\sum}}\left[{a}_{{i}} \left\{{c}^{{n}−\mathrm{1}−{i}} +{b}^{{n}−\mathrm{1}−{i}} −\left({b}+{c}\right)^{{n}−\mathrm{1}−{i}} \right\}\right]+{a}_{{n}−\mathrm{2}} \left\{{c}^{{n}−\mathrm{1}−{n}+\mathrm{2}} +{b}^{{n}−\mathrm{1}−{n}+\mathrm{2}} −\left({b}+{c}\right)^{{n}−\mathrm{1}−{n}+\mathrm{2}} \right\}+{a}_{{n}−\mathrm{1}} \left\{{c}^{{n}−\mathrm{1}−{n}+\mathrm{1}} +{b}^{{n}−\mathrm{1}−{n}+\mathrm{1}} −\left({b}+{c}\right)^{{n}−\mathrm{1}−{n}+\mathrm{1}} \right\}=\mathrm{0} \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{3}} {\sum}}\left[{a}_{{i}} \left\{{c}^{{n}−\mathrm{1}−{i}} +{b}^{{n}−\mathrm{1}−{i}} −\left({b}+{c}\right)^{{n}−\mathrm{1}−{i}} \right\}\right]+{a}_{{n}−\mathrm{2}} \left\{{c}+{b}−\left({b}+{c}\right)\right\}+{a}_{{n}−\mathrm{1}} \left\{\mathrm{1}+\mathrm{1}−\mathrm{1}\right\}=\mathrm{0} \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{3}} {\sum}}\left[{a}_{{i}} \left\{{c}^{{n}−\mathrm{1}−{i}} +{b}^{{n}−\mathrm{1}−{i}} −\left({b}+{c}\right)^{{n}−\mathrm{1}−{i}} \right\}\right]+{a}_{{n}−\mathrm{1}} =\mathrm{0} \\ $$$${a}_{{n}−\mathrm{1}} =\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{3}} {\sum}}\left[{a}_{{i}} \left\{\left({b}+{c}\right)^{{n}−\mathrm{1}−{i}} −{c}^{{n}−\mathrm{1}−{i}} −{b}^{{n}−\mathrm{1}−{i}} \right\}\right] \\ $$$$ \\ $$$${According}\:{to}\:{the}\:{Binomial}\:{Theorem}, \\ $$$$\left({b}+{c}\right)^{{n}−\mathrm{1}−{i}} =\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}−{i}} {\sum}}\begin{pmatrix}{{n}−\mathrm{1}−{i}}\\{{k}}\end{pmatrix}\:{b}^{{n}−\mathrm{1}−{i}−{k}} {c}^{{k}} \\ $$$${or}\:\left({b}+{c}\right)^{{n}−\mathrm{1}−{i}} ={b}^{{n}−\mathrm{1}−{i}} +{c}^{{n}−\mathrm{1}−{i}} +\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{2}−{i}} {\sum}}\begin{pmatrix}{{n}−\mathrm{1}−{i}}\\{{k}}\end{pmatrix}\:{b}^{{n}−\mathrm{1}−{i}−{k}} {c}^{{k}} . \\ $$$$\therefore\:\left({b}+{c}\right)^{{n}−\mathrm{1}−{i}} −{b}^{{n}−\mathrm{1}−{i}} −{c}^{{n}−\mathrm{1}−{i}} =\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{2}−{i}} {\sum}}\begin{pmatrix}{{n}−\mathrm{1}−{i}}\\{{k}}\end{pmatrix}\:{b}^{{n}−\mathrm{1}−{i}−{k}} {c}^{{k}} . \\ $$$${a}_{{n}−\mathrm{1}} =\underset{{i}=\mathrm{0}} {\overset{{n}−\mathrm{3}} {\sum}}\left[{a}_{{i}} \left\{\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{2}−{i}} {\sum}}\begin{pmatrix}{{n}−\mathrm{1}−{i}}\\{{k}}\end{pmatrix}\:{b}^{{n}−\mathrm{1}−{i}−{k}} {c}^{{k}} \right\}\right]\: \\ $$$${a}_{{n}−\mathrm{1}} ={a}_{\mathrm{0}} \left\{\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{2}} {\sum}}\begin{pmatrix}{{n}−\mathrm{1}}\\{{k}}\end{pmatrix}\:{b}^{{n}−\mathrm{1}−{k}} {c}^{{k}} \right\}+{a}_{\mathrm{1}} \left\{\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{3}} {\sum}}\begin{pmatrix}{{n}−\mathrm{2}}\\{{k}}\end{pmatrix}\:{b}^{{n}−\mathrm{2}−{k}} {c}^{{k}} \right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{a}_{\mathrm{2}} \left\{\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{4}} {\sum}}\begin{pmatrix}{{n}−\mathrm{3}}\\{{k}}\end{pmatrix}\:{b}^{{n}−\mathrm{3}−{k}} {c}^{{k}} \right\}+...+{a}_{{n}−\mathrm{4}} \left\{\underset{{k}=\mathrm{1}} {\overset{\mathrm{2}} {\sum}}\begin{pmatrix}{\mathrm{3}}\\{{k}}\end{pmatrix}\:{b}^{\mathrm{3}−{k}} {c}^{{k}} \right\}+{a}_{{n}−\mathrm{3}} \left\{\underset{{k}=\mathrm{1}} {\overset{\mathrm{1}} {\sum}}\begin{pmatrix}{\mathrm{2}}\\{{k}}\end{pmatrix}\:{b}^{\mathrm{2}−{k}} {c}^{{k}} \right\} \\ $$$${Observe}\:{that}\:{the}\:{form}\:{of}\:{the}\:{above}\:{equation} \\ $$$${is}\:{indepedent}\:{of}\:{a}_{{n}−\mathrm{2}} ;\:{so}\:{a}_{{n}−\mathrm{2}} \:{is}\:{a}\:{free} \\ $$$${variable}\:{such}\:{that}\:\mathrm{0}\leqslant{a}_{{n}−\mathrm{2}} \leqslant{min}\left({c}−\mathrm{1},{b}−\mathrm{1}\right). \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$$\boldsymbol{{Proposition}}:\:{For}\:{any}\:{n}\geqslant\mathrm{3},\:{bc}\:{divides}\:\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{2}} {\sum}}\begin{pmatrix}{{n}−\mathrm{1}}\\{{k}}\end{pmatrix}\:{b}^{{n}−\mathrm{1}−{k}} {c}^{{k}} . \\ $$$$\mathrm{Proof}\:\left(\mathrm{induction}\right):\:{Base}\:{case}\:{n}=\mathrm{3}:\:\underset{{k}=\mathrm{1}} {\overset{\mathrm{3}−\mathrm{2}} {\sum}}\begin{pmatrix}{\mathrm{3}−\mathrm{1}}\\{{k}}\end{pmatrix}\:{b}^{\mathrm{3}−\mathrm{1}−{k}} {c}^{{k}} =\begin{pmatrix}{\mathrm{2}}\\{\mathrm{1}}\end{pmatrix}\:{bc} \\ $$$$\Rightarrow{bc}\:{divides}\:\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{2}} {\sum}}\begin{pmatrix}{{n}−\mathrm{1}}\\{{k}}\end{pmatrix}\:{b}^{{n}−\mathrm{1}−{k}} {c}^{{k}} \:{for}\:{n}=\mathrm{3}. \\ $$$$ \\ $$$${Inductive}\:{step}:\:{Suppose}\:{bc}\:{divides}\:\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{2}} {\sum}}\begin{pmatrix}{{j}−\mathrm{1}}\\{{k}}\end{pmatrix}\:{b}^{{j}−\mathrm{1}−{k}} {c}^{{k}} \:{for}\:{n}={j}. \\ $$$${i}.{e}\:\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{2}} {\sum}}\begin{pmatrix}{{j}−\mathrm{1}}\\{{k}}\end{pmatrix}\:{b}^{{j}−\mathrm{1}−{k}} {c}^{{k}} ={rbc}\:{for}\:{some}\:{r}\in\mathbb{N}. \\ $$$${For}\:{n}={j}+\mathrm{1},\:{we}\:{have}\:{that}\:\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{1}} {\sum}}\begin{pmatrix}{{j}}\\{{k}}\end{pmatrix}\:{b}^{{j}−{k}} {c}^{{k}} =\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{1}} {\sum}}\left\{\begin{pmatrix}{{j}−\mathrm{1}}\\{{k}}\end{pmatrix}\:+\begin{pmatrix}{{j}−\mathrm{1}}\\{{k}−\mathrm{1}}\end{pmatrix}\right\}{b}^{{j}−{k}} {c}^{{k}} \\ $$
Commented by Yozzia last updated on 20/Aug/16
$${Let}\:{t}\left({n}\right)=\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{2}} {\sum}}\begin{pmatrix}{{n}−\mathrm{1}}\\{{k}}\end{pmatrix}\:{b}^{{n}−\mathrm{1}−{k}} {c}^{{k}} ,\:{n}\geqslant\mathrm{3}. \\ $$$${Since}\:{bc}\:{divides}\:{t}\left({n}\right)\:{for}\:{n}\geqslant\mathrm{3},{then} \\ $$$${bc}\:{divides}\:{a}_{{n}−\mathrm{1}} \:{since}\:{a}_{{n}−\mathrm{1}} ={a}_{\mathrm{0}} {t}\left({n}\right)+{a}_{\mathrm{1}} {t}\left({n}−\mathrm{1}\right)+{a}_{\mathrm{2}} {t}\left({n}−\mathrm{2}\right)+{a}_{\mathrm{3}} {t}\left({n}−\mathrm{3}\right)+...+{a}_{{n}−\mathrm{3}} {t}\left(\mathrm{3}\right). \\ $$$${Now},\:{b}>\mathrm{1},\:{c}>\mathrm{1}\:{and}\:{all}\:{a}_{{i}} \:\:\left({i}=\mathrm{0},\mathrm{1},\mathrm{2},...\right) \\ $$$${are}\:{non}−{negative}\:{integers},\:{where}\:{min}\left({a}_{\mathrm{0}} \right)=\mathrm{1}. \\ $$$$\therefore{a}_{{n}−\mathrm{1}} ={bcla}_{\mathrm{0}} +...\:\left({l}\in\mathbb{N}\right).\:{But},\:{if}\:{min}\left({a}_{\mathrm{0}} \right)=\mathrm{1}\Rightarrow{a}_{{n}−\mathrm{1}} >{b}\:{and}\:{a}_{{n}−\mathrm{1}} >{c}, \\ $$$${while}\:\mathrm{0}\leqslant{a}_{{n}−\mathrm{1}} \leqslant{min}\left({c}−\mathrm{1},{b}−\mathrm{1}\right)<{min}\left({c},{b}\right). \\ $$$${This}\:{contradiction}\:{indicates}\:{that}\:{q} \\ $$$${cannot}\:{be}\:{a}\:{number}\:{having}\:{digit}\:{length} \\ $$$${n}\geqslant\mathrm{3},\:{and}\:{q}_{{c}} +{q}_{{b}} ={q}_{{b}+{c}} .\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\://// \\ $$
Commented by Yozzia last updated on 20/Aug/16
$$\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{1}} {\sum}}\begin{pmatrix}{{j}}\\{{k}}\end{pmatrix}\:{b}^{{j}−{k}} {c}^{{k}} ={b}\left\{\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{2}} {\sum}}\begin{pmatrix}{{j}−\mathrm{1}}\\{{k}}\end{pmatrix}\:{b}^{{j}−\mathrm{1}−{k}} {c}^{{k}} +\begin{pmatrix}{{j}−\mathrm{1}}\\{{j}−\mathrm{1}}\end{pmatrix}\:{b}^{\mathrm{0}} {c}\right\}+\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{1}} {\sum}}\begin{pmatrix}{{j}−\mathrm{1}}\\{{k}−\mathrm{1}}\end{pmatrix}\:{b}^{{j}−{k}} {c}^{{k}} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{1}} {\sum}}\begin{pmatrix}{{j}}\\{{k}}\end{pmatrix}\:{b}^{{j}−{k}} {c}^{{k}} ={b}×{rbc}+{bc}+\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{1}} {\sum}}\begin{pmatrix}{{j}−\mathrm{1}}\\{{k}−\mathrm{1}}\end{pmatrix}\:{b}^{{j}−{k}} {c}^{{k}} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{1}} {\sum}}\begin{pmatrix}{{j}}\\{{k}}\end{pmatrix}\:{b}^{{j}−{k}} {c}^{{k}} ={bc}\left({br}+\mathrm{1}\right)+\left\{\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{2}} {\sum}}\begin{pmatrix}{{j}−\mathrm{1}}\\{{k}−\mathrm{1}}\end{pmatrix}\:{b}^{{j}−{k}} {c}^{{k}} +\begin{pmatrix}{{j}−\mathrm{1}}\\{{j}−\mathrm{2}}\end{pmatrix}\:{b}^{{j}−{j}+\mathrm{1}} {c}^{{j}−\mathrm{1}} \right\} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{1}} {\sum}}\begin{pmatrix}{{j}}\\{{k}}\end{pmatrix}\:{b}^{{j}−{k}} {c}^{{k}} ={bc}\left({br}+\mathrm{1}\right)+\left({j}−\mathrm{1}\right){bc}^{{j}−\mathrm{1}} +\left\{\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{2}} {\sum}}\begin{pmatrix}{{j}−\mathrm{1}}\\{{k}−\mathrm{1}}\end{pmatrix}\:{b}^{{j}−{k}} {c}^{{k}} \right\} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{1}} {\sum}}\begin{pmatrix}{{j}}\\{{k}}\end{pmatrix}\:{b}^{{j}−{k}} {c}^{{k}} ={bc}\left({br}+\mathrm{1}\right)+\left({j}−\mathrm{1}\right){bc}^{{j}−\mathrm{1}} +{b}^{{j}−\mathrm{1}} {c}+\left\{{c}\begin{pmatrix}{{j}−\mathrm{1}}\\{\mathrm{1}}\end{pmatrix}\:{b}^{{j}−\mathrm{2}} {c}+{c}\begin{pmatrix}{{j}−\mathrm{1}}\\{\mathrm{2}}\end{pmatrix}\:{b}^{{j}−\mathrm{3}} {c}^{\mathrm{2}} +...+{c}\begin{pmatrix}{{j}−\mathrm{1}}\\{{j}−\mathrm{3}}\end{pmatrix}\:{b}^{\mathrm{2}} {c}^{{j}−\mathrm{3}} +\begin{pmatrix}{{j}−\mathrm{1}}\\{{j}−\mathrm{2}}\end{pmatrix}\:{bc}^{{j}−\mathrm{2}} −\begin{pmatrix}{{j}−\mathrm{1}}\\{{j}−\mathrm{2}}\end{pmatrix}\:{bc}^{{j}−\mathrm{2}} \right\} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{1}} {\sum}}\begin{pmatrix}{{j}}\\{{k}}\end{pmatrix}\:{b}^{{j}−{k}} {c}^{{k}} ={bc}\left({br}+\mathrm{1}\right)+\left({j}−\mathrm{1}\right){bc}^{{j}−\mathrm{1}} +{b}^{{j}−\mathrm{1}} {c}+{c}\left\{\begin{pmatrix}{{j}−\mathrm{1}}\\{\mathrm{1}}\end{pmatrix}\:{b}^{{j}−\mathrm{2}} {c}+\begin{pmatrix}{{j}−\mathrm{1}}\\{\mathrm{2}}\end{pmatrix}\:{b}^{{j}−\mathrm{3}} {c}^{\mathrm{2}} +...+\begin{pmatrix}{{j}−\mathrm{1}}\\{{j}−\mathrm{3}}\end{pmatrix}\:{b}^{\mathrm{2}} {c}^{{j}−\mathrm{3}} +\begin{pmatrix}{{j}−\mathrm{1}}\\{{j}−\mathrm{2}}\end{pmatrix}\:{bc}^{{j}−\mathrm{2}} \right\}−\begin{pmatrix}{{j}−\mathrm{1}}\\{{j}−\mathrm{2}}\end{pmatrix}\:{bc}^{{j}−\mathrm{1}} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{1}} {\sum}}\begin{pmatrix}{{j}}\\{{k}}\end{pmatrix}\:{b}^{{j}−{k}} {c}^{{k}} ={bc}\left({br}+\mathrm{1}\right)+\left({j}−\mathrm{1}\right){bc}^{{j}−\mathrm{1}} +{b}^{{j}−\mathrm{1}} {c}+{c}\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{2}} {\sum}}\begin{pmatrix}{{j}−\mathrm{1}}\\{{k}}\end{pmatrix}\:{b}^{{j}−\mathrm{1}−{k}} {c}^{{k}} −\left({j}−\mathrm{1}\right)\:{bc}^{{j}−\mathrm{1}} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{1}} {\sum}}\begin{pmatrix}{{j}}\\{{k}}\end{pmatrix}\:{b}^{{j}−{k}} {c}^{{k}} ={bc}\left({br}+\mathrm{1}+{cr}\right)+{b}^{{j}−\mathrm{1}} {c} \\ $$$${Since}\:{j}\geqslant\mathrm{3}\Rightarrow\:{j}−\mathrm{1}>\mathrm{1}\:\Rightarrow{bc}\:{divides}\:{b}^{{j}−\mathrm{1}} {c}. \\ $$$${Therefore},\:{bc}\:{divides}\:\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{1}} {\sum}}\begin{pmatrix}{{j}}\\{{k}}\end{pmatrix}\:{b}^{{j}−{k}} {c}^{{k}} ,\:{if}\:{bc}\:{divides}\:\underset{{k}=\mathrm{1}} {\overset{{j}−\mathrm{2}} {\sum}}\begin{pmatrix}{{j}−\mathrm{1}}\\{{k}}\end{pmatrix}\:{b}^{{j}−\mathrm{1}−{k}} {c}^{{k}} . \\ $$$${Hence},\:{by}\:{P}.{M}.{I},\:{the}\:{proposition}\:{is}\:{true}. \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$
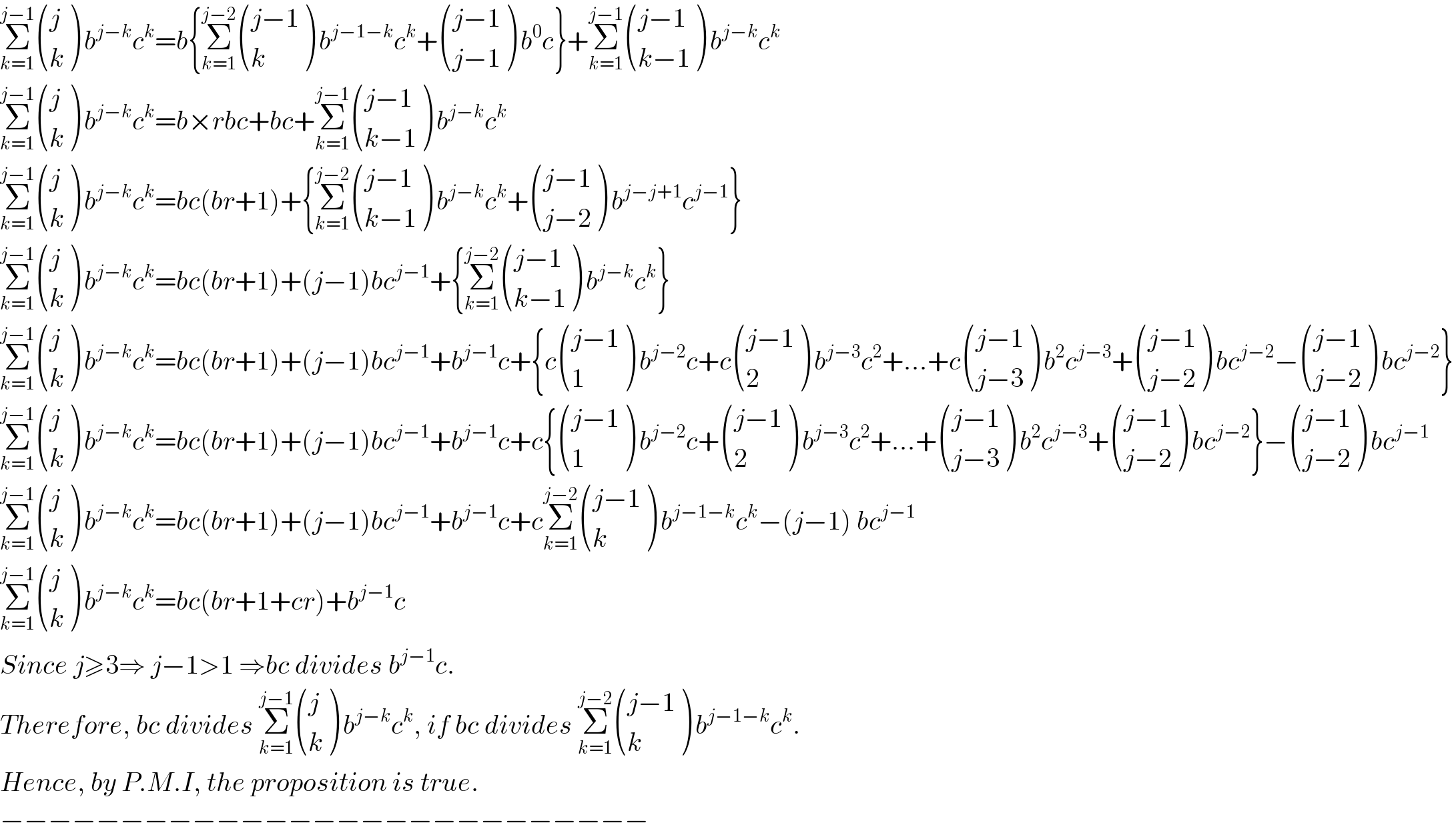
Commented by Rasheed Soomro last updated on 20/Aug/16
$${Wow}!\:{What}\:{a}\:{depth}\:{you}\:{have}\:{in}\:{mathematics}! \\ $$$${Good}\:{wishes}\:{for}\:{you}\:{and}\:{your}\:{future}! \\ $$
Commented by Yozzia last updated on 20/Aug/16
$${Thanks}\:{for}\:{your}\:{kind}\:{words}!\: \\ $$