Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 72492 by petrochengula last updated on 29/Oct/19

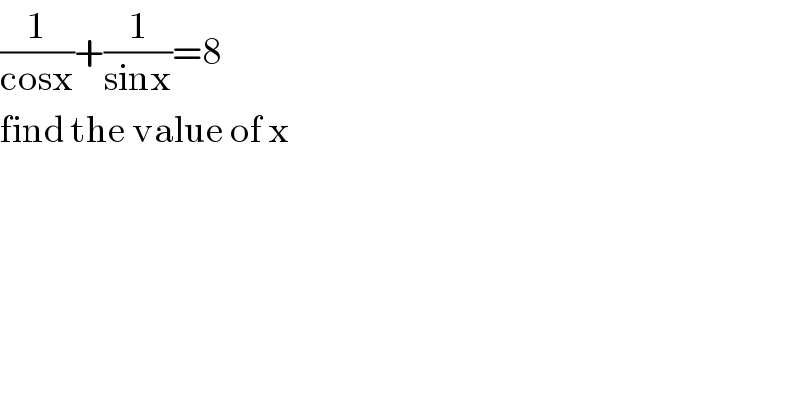
(1/(cosx))+(1/(sinx))=8 find the value of x

$$\frac{\mathrm{1}}{\mathrm{cosx}}+\frac{\mathrm{1}}{\mathrm{sinx}}=\mathrm{8} \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x} \\ $$

Commented by petrochengula last updated on 29/Oct/19

help please

$$\mathrm{help}\:\mathrm{please} \\ $$

Answered by behi83417@gmail.com last updated on 29/Oct/19

sinx+cosx=8sinx.cosx (sinx+cosx)^2 =(8sinx.cosx)^2 1+2sinx.cosx=64sin^2 xcos^2 x [let:sinxcosx=y] 65y^2 =y^2 +2y+1=(y+1)^2 ⇒(√(65))y=±(2y+1)⇒ { ((y=(1/((√(65))−2)))),((y=((−1)/((√(65))+2)))) :} 1)sinx.cosx=(1/((√(65))−2))⇒sin2x=(2/((√(65))−2)) ⇒x=kπ±(1/2)sin^(−1) [(2/((√(65))−2))] (k∈z) 2)sinx.cosx=((−1)/((√(65))+2))⇒sin2x=((−2)/((√(65))+2)) ⇒x=lπ±(1/2)sin^(−1) [((−2)/((√(65))+2))] (l∈z)

$$\mathrm{sinx}+\mathrm{cosx}=\mathrm{8sinx}.\mathrm{cosx} \\ $$$$\left(\mathrm{sinx}+\mathrm{cosx}\right)^{\mathrm{2}} =\left(\mathrm{8sinx}.\mathrm{cosx}\right)^{\mathrm{2}} \\ $$$$\mathrm{1}+\mathrm{2sinx}.\mathrm{cosx}=\mathrm{64sin}^{\mathrm{2}} \mathrm{xcos}^{\mathrm{2}} \mathrm{x}\:\:\:\left[\mathrm{let}:\mathrm{sinxcosx}=\mathrm{y}\right] \\ $$$$\mathrm{65y}^{\mathrm{2}} =\mathrm{y}^{\mathrm{2}} +\mathrm{2y}+\mathrm{1}=\left(\mathrm{y}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\sqrt{\mathrm{65}}\mathrm{y}=\pm\left(\mathrm{2y}+\mathrm{1}\right)\Rightarrow\begin{cases}{\mathrm{y}=\frac{\mathrm{1}}{\sqrt{\mathrm{65}}−\mathrm{2}}}\\{\mathrm{y}=\frac{−\mathrm{1}}{\sqrt{\mathrm{65}}+\mathrm{2}}}\end{cases} \\ $$$$\left.\mathrm{1}\right)\mathrm{sinx}.\mathrm{cosx}=\frac{\mathrm{1}}{\sqrt{\mathrm{65}}−\mathrm{2}}\Rightarrow\mathrm{sin2x}=\frac{\mathrm{2}}{\sqrt{\mathrm{65}}−\mathrm{2}} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{k}\pi\pm\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left[\frac{\mathrm{2}}{\sqrt{\mathrm{65}}−\mathrm{2}}\right]\:\:\left(\mathrm{k}\in\mathrm{z}\right) \\ $$$$\left.\mathrm{2}\right)\mathrm{sinx}.\mathrm{cosx}=\frac{−\mathrm{1}}{\sqrt{\mathrm{65}}+\mathrm{2}}\Rightarrow\mathrm{sin2x}=\frac{−\mathrm{2}}{\sqrt{\mathrm{65}}+\mathrm{2}} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{l}\pi\pm\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}^{−\mathrm{1}} \left[\frac{−\mathrm{2}}{\sqrt{\mathrm{65}}+\mathrm{2}}\right]\:\:\:\:\left(\mathrm{l}\in\mathrm{z}\right) \\ $$

Commented by petrochengula last updated on 29/Oct/19

thanks

$$\mathrm{thanks} \\ $$

Answered by Tanmay chaudhury last updated on 29/Oct/19

sinx+cosx=4(2sinxcosx) (√(1+sin2x)) =4sin2x 1+a=16a^2 →16a^2 −a−1=0 a=((1±(√(1−4.16.(−1))))/(2×16))=((1±(√(65)))/(32)) (√(65)) ≈8.06 a=((9.06)/(32)),((−7.06)/(32)) a≈0.28,−0.22 sin2x=0.28=sin(0.284) [note angle in radian 2x=0.284→x=0.142 took help of calculator

$${sinx}+{cosx}=\mathrm{4}\left(\mathrm{2}{sinxcosx}\right) \\ $$$$\sqrt{\mathrm{1}+{sin}\mathrm{2}{x}}\:=\mathrm{4}{sin}\mathrm{2}{x} \\ $$$$\mathrm{1}+{a}=\mathrm{16}{a}^{\mathrm{2}} \rightarrow\mathrm{16}{a}^{\mathrm{2}} −{a}−\mathrm{1}=\mathrm{0} \\ $$$${a}=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}−\mathrm{4}.\mathrm{16}.\left(−\mathrm{1}\right)}}{\mathrm{2}×\mathrm{16}}=\frac{\mathrm{1}\pm\sqrt{\mathrm{65}}}{\mathrm{32}} \\ $$$$\sqrt{\mathrm{65}}\:\approx\mathrm{8}.\mathrm{06}\: \\ $$$${a}=\frac{\mathrm{9}.\mathrm{06}}{\mathrm{32}},\frac{−\mathrm{7}.\mathrm{06}}{\mathrm{32}} \\ $$$${a}\approx\mathrm{0}.\mathrm{28},−\mathrm{0}.\mathrm{22} \\ $$$${sin}\mathrm{2}{x}=\mathrm{0}.\mathrm{28}={sin}\left(\mathrm{0}.\mathrm{284}\right)\:\:\:\left[{note}\:{angle}\:{in}\:{radian}\right. \\ $$$$\mathrm{2}{x}=\mathrm{0}.\mathrm{284}\rightarrow{x}=\mathrm{0}.\mathrm{142} \\ $$$${took}\:{help}\:{of}\:{calculator} \\ $$

Commented by petrochengula last updated on 29/Oct/19

thanks

$$\mathrm{thanks} \\ $$

Commented by Tanmay chaudhury last updated on 29/Oct/19

most welcome...

$${most}\:{welcome}... \\ $$

Answered by MJS last updated on 29/Oct/19

x=2arctan t ⇒ cos x =((1−t^2 )/(1+t^2 )); sin x =((2t)/(1+t^2 )) ((1+t^2 )/(1−t^2 ))+((1+t^2 )/(2t))=8 transforming ⇒ t^4 −18t^3 +14t−1=0 we can exactly solve this (t^2 −(9+(√(65)))t−(8+(√(65))))(t^2 −(9−(√(65)))t−(8r−(√(65))))=0 t_(1, 2) =((9+(√(65)))/2)±((√(178+22(√(65))))/2) t_(3, 4) =((9−(√(65)))/2)±((√(178−22(√(65))))/2) x_i =2πn+2arctan t with n∈Z ⇒ x_1 ≈−1.45953+2πn x_2 ≈3.03033+2πn x_3 ≈.143562+2πn x_4 ≈1.42723+2πn

$${x}=\mathrm{2arctan}\:{t}\:\Rightarrow\:\mathrm{cos}\:{x}\:=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} };\:\mathrm{sin}\:{x}\:=\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{1}−{t}^{\mathrm{2}} }+\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{2}{t}}=\mathrm{8} \\ $$$$\mathrm{transforming}\:\Rightarrow \\ $$$${t}^{\mathrm{4}} −\mathrm{18}{t}^{\mathrm{3}} +\mathrm{14}{t}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{exactly}\:\mathrm{solve}\:\mathrm{this} \\ $$$$\left({t}^{\mathrm{2}} −\left(\mathrm{9}+\sqrt{\mathrm{65}}\right){t}−\left(\mathrm{8}+\sqrt{\mathrm{65}}\right)\right)\left({t}^{\mathrm{2}} −\left(\mathrm{9}−\sqrt{\mathrm{65}}\right){t}−\left(\mathrm{8}{r}−\sqrt{\mathrm{65}}\right)\right)=\mathrm{0} \\ $$$${t}_{\mathrm{1},\:\mathrm{2}} =\frac{\mathrm{9}+\sqrt{\mathrm{65}}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{178}+\mathrm{22}\sqrt{\mathrm{65}}}}{\mathrm{2}} \\ $$$${t}_{\mathrm{3},\:\mathrm{4}} =\frac{\mathrm{9}−\sqrt{\mathrm{65}}}{\mathrm{2}}\pm\frac{\sqrt{\mathrm{178}−\mathrm{22}\sqrt{\mathrm{65}}}}{\mathrm{2}} \\ $$$${x}_{{i}} =\mathrm{2}\pi{n}+\mathrm{2arctan}\:{t}\:\mathrm{with}\:{n}\in\mathbb{Z} \\ $$$$\Rightarrow \\ $$$${x}_{\mathrm{1}} \approx−\mathrm{1}.\mathrm{45953}+\mathrm{2}\pi{n} \\ $$$${x}_{\mathrm{2}} \approx\mathrm{3}.\mathrm{03033}+\mathrm{2}\pi{n} \\ $$$${x}_{\mathrm{3}} \approx.\mathrm{143562}+\mathrm{2}\pi{n} \\ $$$${x}_{\mathrm{4}} \approx\mathrm{1}.\mathrm{42723}+\mathrm{2}\pi{n} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com