
Question and Answers Forum
Question Number 72497 by Shamim last updated on 29/Oct/19
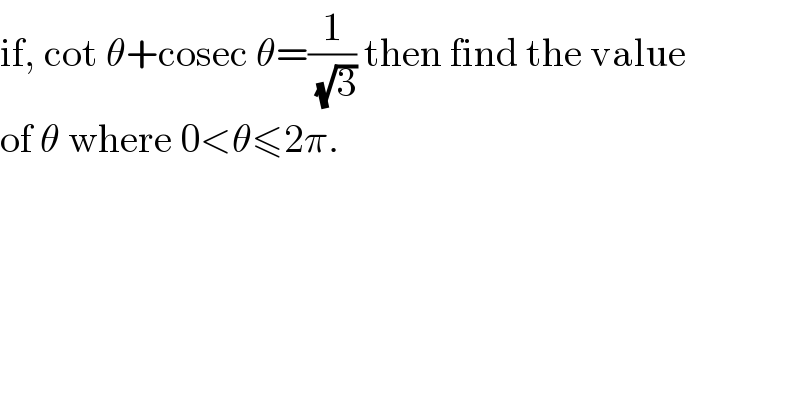
Answered by behi83417@gmail.com last updated on 29/Oct/19
![((cosθ)/(sinθ))+(1/(sinθ))=(1/(√3))⇒((1+cosθ)/(sinθ))=(1/(√3))⇒ ((2cos^2 (θ/2))/(2sin(θ/2)cos(θ/2)))=(1/(√3))⇒ { ((1.cos(θ/2)=0)),((2.cot(θ/2)=(1/(√3)))) :} 1) cos(θ/2)=0⇒(θ/2)=±(π/2)+kπ⇒θ=kπ±π [for:k=0,1⇒θ=0^• [not ok],π,2π] 2)cot(θ/2)=(1/(√3))=cot(π/3)⇒(θ/2)=(π/3)+lπ ⇒[θ=((2π)/3)+2lπ,for:l=0,1⇒θ=((2π)/3),((5π)/3)]](Q72504.png)
Answered by Tanmay chaudhury last updated on 29/Oct/19

Answered by MJS last updated on 29/Oct/19
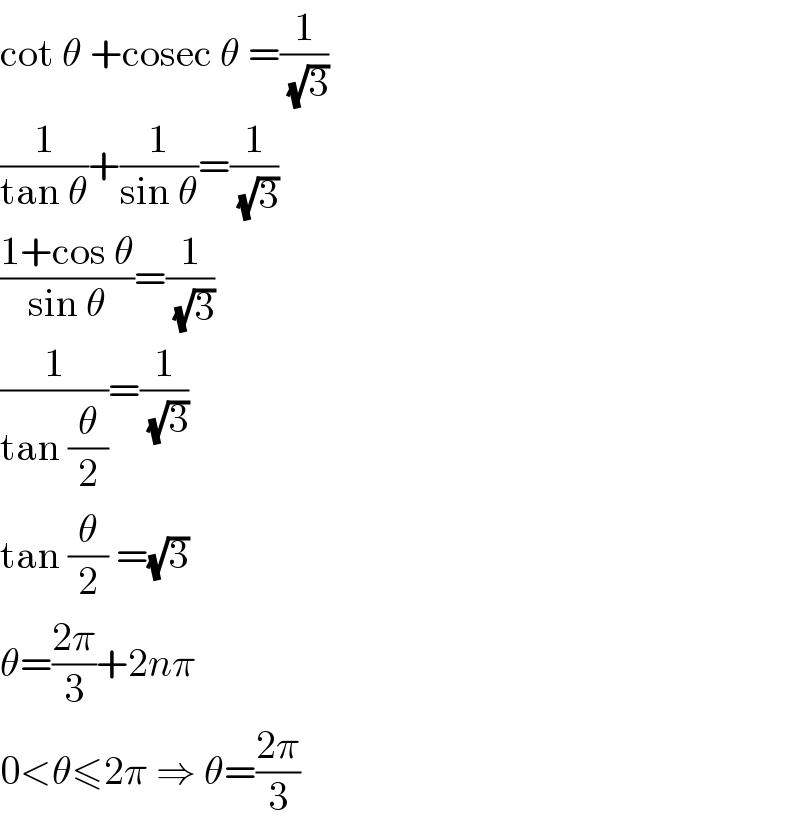
| ||
Question and Answers Forum | ||
Question Number 72497 by Shamim last updated on 29/Oct/19 | ||
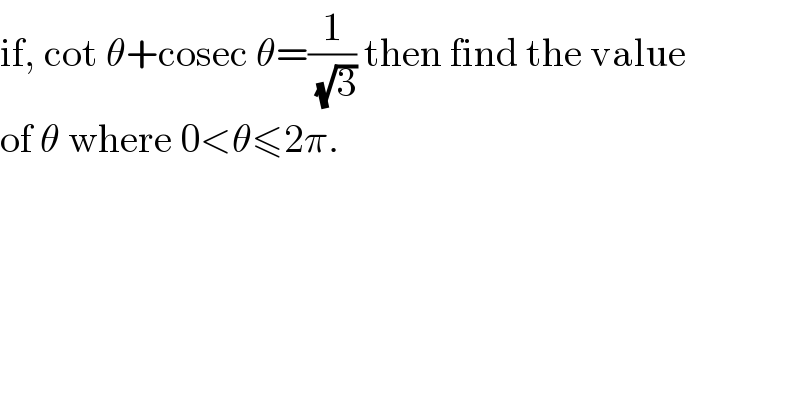 | ||
Answered by behi83417@gmail.com last updated on 29/Oct/19 | ||
![((cosθ)/(sinθ))+(1/(sinθ))=(1/(√3))⇒((1+cosθ)/(sinθ))=(1/(√3))⇒ ((2cos^2 (θ/2))/(2sin(θ/2)cos(θ/2)))=(1/(√3))⇒ { ((1.cos(θ/2)=0)),((2.cot(θ/2)=(1/(√3)))) :} 1) cos(θ/2)=0⇒(θ/2)=±(π/2)+kπ⇒θ=kπ±π [for:k=0,1⇒θ=0^• [not ok],π,2π] 2)cot(θ/2)=(1/(√3))=cot(π/3)⇒(θ/2)=(π/3)+lπ ⇒[θ=((2π)/3)+2lπ,for:l=0,1⇒θ=((2π)/3),((5π)/3)]](Q72504.png) | ||
| ||
Answered by Tanmay chaudhury last updated on 29/Oct/19 | ||
 | ||
| ||
Answered by MJS last updated on 29/Oct/19 | ||
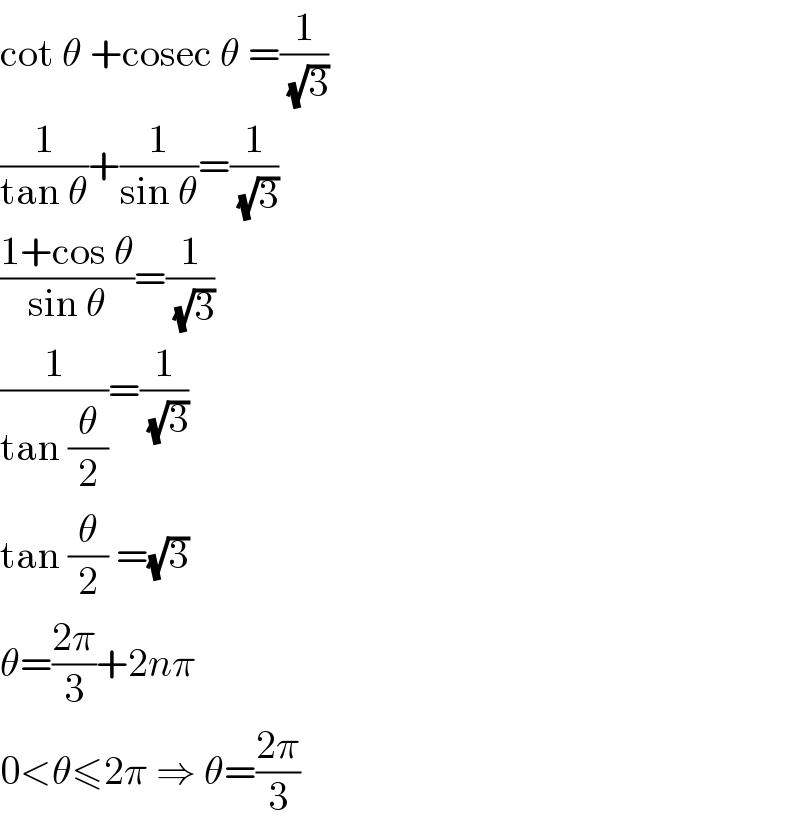 | ||
| ||