
Question Number 7263 by Tawakalitu. last updated on 19/Aug/16

Commented by Rasheed Soomro last updated on 20/Aug/16

$${I}\:{have}\:{answered}\:{your}\:{question}#\mathrm{6852} \\ $$$${which}\:{is}\:{very}\:{resembling}\:{to}\:{this}\:{question}. \\ $$$${Please}\:{see}\:{if}\:{you}\:{have}\:{not}\:{seen}\:{yet}. \\ $$
Commented by Rasheed Soomro last updated on 20/Aug/16
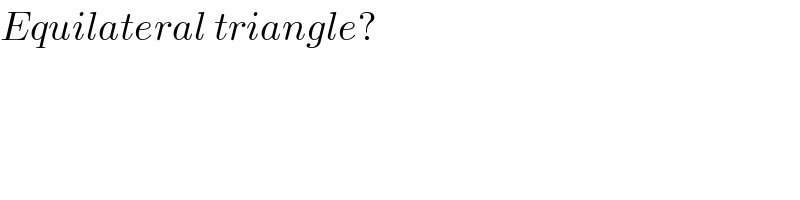
$${Equilateral}\:{triangle}? \\ $$
Answered by Rasheed Soomro last updated on 23/Aug/16

$${Angles}\:{in}\:{terms}\:{of}\:{a},{b},{x}\:{and}\:\:{y}. \\ $$$$\left({For}\:{diagram}\:{see}\:{the}\:{comment}\:{below}\right) \\ $$$${Assumed}\:{that}\:{the}\:{given}\:{triangle}\:{is}\:{equilateral}. \\ $$$$\mathcal{I}-\mathcal{E}\:\:{AB}={BC}={AC}\Rightarrow\angle{A}=\angle{B}=\angle{C}=\mathrm{60}° \\ $$$${a}+{c}=\angle{A}=\mathrm{60}\Rightarrow\:{c}=\mathrm{60}−{a} \\ $$$${b}+{d}=\angle{B}=\mathrm{60}\Rightarrow\:{d}=\mathrm{60}−{b} \\ $$$${In}\:\bigtriangleup{ABF}:{a}+{b}+\angle\mathrm{1}=\mathrm{180}\Rightarrow\angle\mathrm{1}=\mathrm{180}−{a}−{b} \\ $$$$\left({Other}\:\angle\mathrm{1}\:{is}\:{vertical}\:{angle}\:{of}\:{this}.\right) \\ $$$$\angle\mathrm{1}+\angle\mathrm{2}=\mathrm{180}\Rightarrow\angle\mathrm{2}=\mathrm{180}−\angle\mathrm{1}={a}+{b} \\ $$$${In}\:\bigtriangleup{AFB}:{c}+\angle\mathrm{2}+\angle\mathrm{3}=\mathrm{180}\Rightarrow\angle\mathrm{3}=\mathrm{180}−\angle\mathrm{2}−{c} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{180}−{a}−{b}−\mathrm{60}+{a}\:=\mathrm{120}−{b} \\ $$$${In}\:\bigtriangleup{BFE}:{d}+\angle\mathrm{2}+\angle\mathrm{4}=\mathrm{180}\Rightarrow\angle\mathrm{4}=\mathrm{180}−\angle\mathrm{2}−{d} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{180}−{a}−{b}−\mathrm{60}+{b}\:=\mathrm{120}−{a} \\ $$$$\angle\mathrm{3}+{x}+\angle\mathrm{5}=\mathrm{180}:\angle\mathrm{5}=\mathrm{180}−\angle\mathrm{3}−{x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{180}−\mathrm{120}+{b}−{x}=\mathrm{60}+{b}−{x} \\ $$$${In}\:\bigtriangleup{DEF}:{x}+{y}+\angle\mathrm{1}=\mathrm{180}\Rightarrow{y}=\mathrm{180}−{x}−\angle\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{180}−{x}−\mathrm{180}+{a}+{b}={a}+{b}−{x} \\ $$$$\angle\mathrm{4}+{y}+\angle\mathrm{6}=\mathrm{180}:\angle\mathrm{6}=\mathrm{180}−\angle\mathrm{4}−{y} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{180}−\mathrm{120}+{a}−{a}−{b}+{x}=\mathrm{60}−{b}+{x} \\ $$$$\mathcal{D}{etermining}\:{x}\:{and}\:\:{y} \\ $$$${In}\:\bigtriangleup{AEC},\:{according}\:{to}\:{sine}\:{law}: \\ $$$$\left({Let}\:{AB}={BC}={AC}=\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{CE}}{\mathrm{sin}\:{c}}=\frac{{AC}}{\mathrm{sin}\left({y}+\angle\mathrm{6}\right)\:} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{{CE}}{\mathrm{sin}\left(\mathrm{60}−{a}\right)\:}=\frac{\mathrm{1}}{\mathrm{sin}\left({a}+{b}−{x}+\mathrm{60}−{b}+{x}\right)\:}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{{CE}}{\mathrm{sin}\left(\mathrm{60}−{a}\right)\:}=\frac{\mathrm{1}}{\mathrm{sin}\left({a}+\mathrm{60}\right)\:} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{CE}=\frac{\mathrm{sin}\left(\mathrm{60}−{a}\right)}{\mathrm{sin}\left(\mathrm{60}+{a}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{sin}\:\mathrm{60}\:\mathrm{cos}\:{a}−\mathrm{cos}\:\mathrm{60}\:\mathrm{sin}\:{a}}{\mathrm{sin}\:\mathrm{60}\:\mathrm{cos}\:{a}+\mathrm{cos}\:\mathrm{60}\:\mathrm{sin}\:{a}} \\ $$$${In}\:\bigtriangleup{BDC},\:{by}\:{sine}\:{law}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\frac{{CD}}{\mathrm{sin}\:{d}}=\frac{{BC}}{\mathrm{sin}\left({x}+\angle\mathrm{5}\right)\:} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\frac{{CD}}{\mathrm{sin}\left(\mathrm{60}−{b}\right)\:}=\frac{\mathrm{1}}{\mathrm{sin}\left({x}+\mathrm{60}+{b}−{x}\right)\:} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{CD}=\frac{\mathrm{sin}\left(\mathrm{60}−{b}\right)}{\mathrm{sin}\left(\mathrm{60}+{b}\right)\:} \\ $$$${In}\:\bigtriangleup{CDE},{by}\:{sine}\:{law} \\ $$$$\:\:\:\:\:\:\:\frac{{CD}}{\mathrm{sin}\:\angle\mathrm{6}}=\frac{{CE}}{\mathrm{sin}\:\angle\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\frac{{CD}}{{CE}}=\frac{\mathrm{sin}\:\angle\mathrm{6}}{\mathrm{sin}\:\angle\mathrm{5}} \\ $$$$\:\:\:\:\frac{\mathrm{sin}\left(\mathrm{60}−{b}\right)}{\mathrm{sin}\left(\mathrm{60}+{b}\right)\:}/\frac{\mathrm{sin}\left(\mathrm{60}−{a}\right)}{\mathrm{sin}\left(\mathrm{60}+{a}\right)}=\frac{\mathrm{sin}\left(\mathrm{60}−{b}+{x}\right)}{\mathrm{sin}\left(\mathrm{60}+{b}−{x}\right)} \\ $$$$\frac{\mathrm{sin}\left(\mathrm{60}−{b}\right)\:\mathrm{sin}\left(\mathrm{60}+{a}\right)}{\mathrm{sin}\left(\mathrm{60}+{b}\right)\:\mathrm{sin}\left(\mathrm{60}−{a}\right)}=\frac{\mathrm{sin}\left(\mathrm{60}−{b}+{x}\right)}{\mathrm{sin}\left(\mathrm{60}+{b}−{x}\right)}=\frac{\mathrm{sin}\left(\mathrm{60}−\left({b}−{x}\right)\right)\:}{\mathrm{sin}\left(\mathrm{60}+\left({b}−{x}\right)\:\right.} \\ $$$$\frac{\mathrm{sin}\left(\mathrm{60}−{b}\right)\:\mathrm{sin}\left(\mathrm{60}+{a}\right)\left(\overset{{Let}} {={A}}\right)}{\mathrm{sin}\left(\mathrm{60}+{b}\right)\:\mathrm{sin}\left(\mathrm{60}−{a}\right)\left(\overset{{Let}} {={B}}\right)}=\frac{\mathrm{sin}\:\mathrm{60}\:\mathrm{cos}\left({b}−{x}\right)−\mathrm{cos}\:\mathrm{60}\:\mathrm{sin}\left({b}−{x}\right)\:\:}{\mathrm{sin}\:\mathrm{60}\:\mathrm{cos}\left({b}−{x}\right)+\mathrm{cos}\:\mathrm{60}\:\mathrm{sin}\left({b}−{x}\right)} \\ $$$$\:\:\:\:\frac{{A}}{{B}}=\frac{\mathrm{sin}\:\mathrm{60}\:\mathrm{cos}\left({b}−{x}\right)−\mathrm{cos}\:\mathrm{60}\:\mathrm{sin}\left({b}−{x}\right)}{\mathrm{sin}\:\mathrm{60}\:\mathrm{cos}\left({b}−{x}\right)+\mathrm{cos}\:\mathrm{60}\:\mathrm{sin}\left({b}−{x}\right)} \\ $$$${Continu}\:{to}\:{my}\:{comment}\:{below}. \\ $$
Commented by Rasheed Soomro last updated on 20/Aug/16

Commented by Tawakalitu. last updated on 21/Aug/16

$${Wow},\:{thank}\:{you}\:{for}\:{your}\:{help} \\ $$
Commented by Tawakalitu. last updated on 21/Aug/16
$${looking}\:{forward}\:{for}\:{the}\:{remaining}\:{solution}. \\ $$
Commented by Tawakalitu. last updated on 21/Aug/16
$${i}\:{really}\:{appreciate}\:{your}\:{effort} \\ $$
Commented by Tawakalitu. last updated on 21/Aug/16

$${God}\:{bless}\:{you} \\ $$
Commented by Tawakalitu. last updated on 21/Aug/16

$${Am}\:{with}\:{you}\:{sir} \\ $$
Commented by Tawakalitu. last updated on 21/Aug/16
$${Thanks}\:{so}\:{much}\:{sir}. \\ $$
Commented by Rasheed Soomro last updated on 22/Aug/16
![Continue from answer (A/B)=((sin 60 cos(b−x)−cos 60 sin(b−x))/(sin 60 cos(b−x)+cos 60 sin(b−x))) (A/B)=((1−((cos 60 sin(b−x))/(sin 60 cos(b−x))))/(1+((cos 60 sin(b−x))/(sin 60 cos(b−x))))) A+Acot 60 tan(b−x)=B−Bcot 60 tan(b−x) Acot 60 tan(b−x)+Bcot 60 tan(b−x)=B−A cot 60 tan(b−x)[A+B]=B−A cot 60 tan(b−x)=((B−A)/(B+A)) tan(b−x)=((B−A)/((B+A)cot 60)) b−x=tan^(−1) (((B−A)/((B+A)cot 60))) x=b−tan^(−1) (((B−A)/((B+A)×((√3)/3)))) x=b−tan^(−1) (((3(B−A))/((√3)(B+A)))) In △DEF, y+x+∠1=180 y=180−x−∠1 y=180−(b−tan^(−1) (((B−A)/((B+A)cot 60))))−(180−a−b) y=180−b+tan^(−1) (((B−A)/((B+A)cot 60)))−180+a+b) y=a+tan^(−1) (((B−A)/((B+A)×((√3)/3)))) y=a+tan^(−1) (((3(B−A))/((√3)(B+A)))) x=b−tan^(−1) (((3(B−A))/((√3)(B+A)))) Where A=sin(60−b) sin(60+a) B=sin(60+b) sin(60−a) Answer completed.](Q7292.png)
$${Continue}\:{from}\:{answer} \\ $$$$\frac{{A}}{{B}}=\frac{\mathrm{sin}\:\mathrm{60}\:\mathrm{cos}\left({b}−{x}\right)−\mathrm{cos}\:\mathrm{60}\:\mathrm{sin}\left({b}−{x}\right)}{\mathrm{sin}\:\mathrm{60}\:\mathrm{cos}\left({b}−{x}\right)+\mathrm{cos}\:\mathrm{60}\:\mathrm{sin}\left({b}−{x}\right)} \\ $$$$\frac{{A}}{{B}}=\frac{\mathrm{1}−\frac{\mathrm{cos}\:\mathrm{60}\:\mathrm{sin}\left({b}−{x}\right)}{\mathrm{sin}\:\mathrm{60}\:\mathrm{cos}\left({b}−{x}\right)}}{\mathrm{1}+\frac{\mathrm{cos}\:\mathrm{60}\:\mathrm{sin}\left({b}−{x}\right)}{\mathrm{sin}\:\mathrm{60}\:\mathrm{cos}\left({b}−{x}\right)}} \\ $$$${A}+{A}\mathrm{cot}\:\mathrm{60}\:\mathrm{tan}\left({b}−{x}\right)={B}−{B}\mathrm{cot}\:\mathrm{60}\:\mathrm{tan}\left({b}−{x}\right) \\ $$$${A}\mathrm{cot}\:\mathrm{60}\:\mathrm{tan}\left({b}−{x}\right)+{B}\mathrm{cot}\:\mathrm{60}\:\mathrm{tan}\left({b}−{x}\right)={B}−{A} \\ $$$$\mathrm{cot}\:\mathrm{60}\:\mathrm{tan}\left({b}−{x}\right)\left[{A}+{B}\right]={B}−{A} \\ $$$$\mathrm{cot}\:\mathrm{60}\:\mathrm{tan}\left({b}−{x}\right)=\frac{{B}−{A}}{{B}+{A}} \\ $$$$\mathrm{tan}\left({b}−{x}\right)=\frac{{B}−{A}}{\left({B}+{A}\right)\mathrm{cot}\:\mathrm{60}} \\ $$$${b}−{x}=\mathrm{tan}^{−\mathrm{1}} \left(\frac{{B}−{A}}{\left({B}+{A}\right)\mathrm{cot}\:\mathrm{60}}\right) \\ $$$${x}={b}−\mathrm{tan}^{−\mathrm{1}} \left(\frac{{B}−{A}}{\left({B}+{A}\right)×\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}}\right) \\ $$$${x}={b}−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}\left({B}−{A}\right)}{\sqrt{\mathrm{3}}\left({B}+{A}\right)}\right) \\ $$$${In}\:\bigtriangleup{DEF}, \\ $$$$\:\:\:\:\:\:\:{y}+{x}+\angle\mathrm{1}=\mathrm{180} \\ $$$$\:\:\:\:\:\:{y}=\mathrm{180}−{x}−\angle\mathrm{1} \\ $$$$\:\:\:\:\:{y}=\mathrm{180}−\left({b}−\mathrm{tan}^{−\mathrm{1}} \left(\frac{{B}−{A}}{\left({B}+{A}\right)\mathrm{cot}\:\mathrm{60}}\right)\right)−\left(\mathrm{180}−{a}−{b}\right) \\ $$$$\left.\:\:\:\:\:{y}=\mathrm{180}−{b}+\mathrm{tan}^{−\mathrm{1}} \left(\frac{{B}−{A}}{\left({B}+{A}\right)\mathrm{cot}\:\mathrm{60}}\right)−\mathrm{180}+{a}+{b}\right) \\ $$$$ \\ $$$$\:\:\:\:\:\:\:{y}={a}+\mathrm{tan}^{−\mathrm{1}} \left(\frac{{B}−{A}}{\left({B}+{A}\right)×\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}}\right) \\ $$$$\:\:\:\:\:\:\:{y}={a}+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}\left({B}−{A}\right)}{\sqrt{\mathrm{3}}\left({B}+{A}\right)}\right) \\ $$$$\:\:\:\:\:\:\:{x}={b}−\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{3}\left({B}−{A}\right)}{\sqrt{\mathrm{3}}\left({B}+{A}\right)}\right) \\ $$$$ \\ $$$${Where}\:\:{A}=\mathrm{sin}\left(\mathrm{60}−{b}\right)\:\mathrm{sin}\left(\mathrm{60}+{a}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{B}=\mathrm{sin}\left(\mathrm{60}+{b}\right)\:\mathrm{sin}\left(\mathrm{60}−{a}\right) \\ $$$$ \\ $$$$ \\ $$$${Answer}\:{completed}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$
Commented by Tawakalitu. last updated on 23/Aug/16
$${Seriously}\:{this}\:{is}\:{a}\:{great}\:{work}.\:{God}\:{will}\:{help}\:{you}\:{too} \\ $$
