∫_( 2) ^( 3) ((tan^(−1) (x))/(1 − x^2 )) dx


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 72665 by TawaTawa last updated on 31/Oct/19

$\int_{2}^{3} \frac{\tan^{- 1} (x)}{1 - x^{2}} dx$
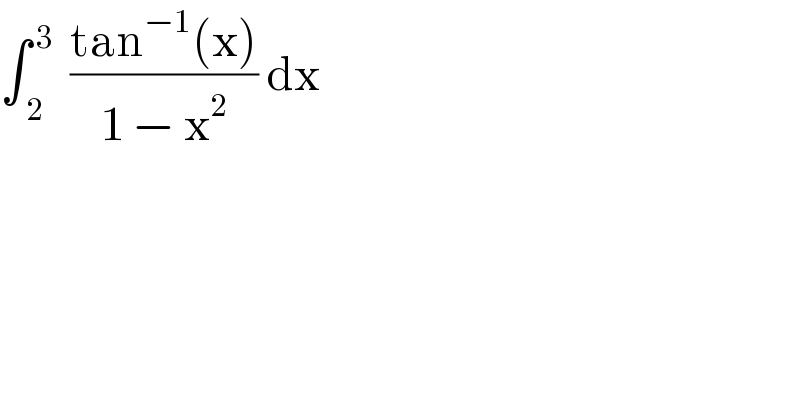
Commented by mind is power last updated on 31/Oct/19

$non close value we have to use {Li}_{2} (x) function$
Commented by TawaTawa last updated on 31/Oct/19

$Help sir$
Commented by mathmax by abdo last updated on 31/Oct/19
$let I =∫_2 ^3 ((arctan(x))/(1−x^2 ))dx =_(x=2+t) ∫_0 ^1 ((arctan(2+t))/(1−(2+t)^2 ))dt =−∫_0 ^1 ((arctan(2+t))/((t+2)^2 −1))dt =−∫_0 ^1 ((arctan(t+2))/((t+1)(t+3)))dt =−(1/2)∫_0 ^1 arctan(t+2)((1/(t+1))−(1/(t+3)))dt =(1/2)∫_0 ^1 ((arctan(t+2))/(t+3))dt−(1/2)∫_0 ^1 ((arctan(t+2))/(t+1))dt =(1/2)H−(1/2)K H=∫_0 ^1 ((arctan(t+2))/(t+3))dt and K=∫_0 ^1 ((arctan(t+2))/(t+1))dt let f(x)=∫_0 ^1 ((arctan(t+x))/(t+3))dt with x≥0 ⇒ f^′ (x)=∫_0 ^1 (1/((t+3)(1+(t+x)^2 )))dt =∫_0 ^1 (dt/((t+3)(t^2 +2xt +x^2 +1))) let decompose F(t)=(1/((t+3)(t^2 +2xt +x^2 +1))) F(t)=(a/(t+3)) +((bt +c)/(t^2 +2xt +x^2 +1)) a =(1/(10−6x +x^2 )) lim_(t→+∞) tF(t)=0=a+b ⇒b=((−1)/(x^2 −6x +10)) F(0)=(1/(3(x^2 +1))) =(a/3) +(c/(x^2 +1)) ⇒(1/3) =((x^2 +1)/3)a +c ⇒ 1=(x^2 +1)a +3c ⇒3c=1−(x^2 +1)×(1/(x^2 −6x +10)) ⇒c =(1/3)(1−((x^2 +1)/(x^2 −6x +10))) ∫_0 ^1 F(t)dt =a ∫_0 ^1 (dt/(t+3)) +(b/2) ∫_0 ^1 ((2t +2x−2x )/(t^2 +2xt +x^2 +1))dt =a[ln(t+3)]_0 ^1 +(b/2)ln(t^2 +2xt +x^2 +1)]_0 ^x +c ∫_0 ^1 (dt/(t^2 +2xt +x^2 +1)) ∫_0 ^1 (dt/(t^2 +2xt +x^2 +1)) =∫_0 ^1 (dt/((t+x)^2 +1)) =_(t+x=u) ∫_x ^(x+1) (du/(1+u^2 )) =arctan(x+1)−arctanx ⇒ f^′ (x)=a{ln((4/3))}+(b/2)(ln(4x^2 +1)−ln(x^2 +1)+c(arctan(x+1)−arctanx) ⇒f(x)=aln((4/3))x +(b/2)∫ln(((4x^2 +1)/(x^2 +1)))dx +c∫ (arctan(x+1)−arctan(x))dx +c ....be continued....$
$l e t I = \int_{2}^{3} \frac{a r c t a n (x)}{1 - x^{2}} d x =_{x = 2 + t} \int_{0}^{1} \frac{a r c t a n (2 + t)}{1 - {(2 + t)}^{2}} d t$ $= - \int_{0}^{1} \frac{a r c t a n (2 + t)}{{(t + 2)}^{2} - 1} d t = - \int_{0}^{1} \frac{a r c t a n (t + 2)}{(t + 1) (t + 3)} d t$ $= - \frac{1}{2} \int_{0}^{1} a r c t a n (t + 2) (\frac{1}{t + 1} - \frac{1}{t + 3}) d t$ $= \frac{1}{2} \int_{0}^{1} \frac{a r c t a n (t + 2)}{t + 3} d t - \frac{1}{2} \int_{0}^{1} \frac{a r c t a n (t + 2)}{t + 1} d t$ $= \frac{1}{2} H - \frac{1}{2} K$ $H = \int_{0}^{1} \frac{a r c t a n (t + 2)}{t + 3} d t a n d K = \int_{0}^{1} \frac{a r c t a n (t + 2)}{t + 1} d t$ $l e t f (x) = \int_{0}^{1} \frac{a r c t a n (t + x)}{t + 3} d t w i t h x ⩾ 0 \Rightarrow$ $f^{^{'}} (x) = \int_{0}^{1} \frac{1}{(t + 3) (1 + {(t + x)}^{2})} d t = \int_{0}^{1} \frac{d t}{(t + 3) (t^{2} + 2 x t + x^{2} + 1)}$ $l e t d e c o m p o s e F (t) = \frac{1}{(t + 3) (t^{2} + 2 x t + x^{2} + 1)}$ $F (t) = \frac{a}{t + 3} + \frac{b t + c}{t^{2} + 2 x t + x^{2} + 1}$ $a = \frac{1}{10 - 6 x + x^{2}}$ ${l i m}_{t \to + \infty} t F (t) = 0 = a + b \Rightarrow b = \frac{- 1}{x^{2} - 6 x + 10}$ $F (0) = \frac{1}{3 (x^{2} + 1)} = \frac{a}{3} + \frac{c}{x^{2} + 1} \Rightarrow \frac{1}{3} = \frac{x^{2} + 1}{3} a + c \Rightarrow$ $1 = (x^{2} + 1) a + 3 c \Rightarrow 3 c = 1 - (x^{2} + 1) \times \frac{1}{x^{2} - 6 x + 10}$ $\Rightarrow c = \frac{1}{3} (1 - \frac{x^{2} + 1}{x^{2} - 6 x + 10})$ $\int_{0}^{1} F (t) d t = a \int_{0}^{1} \frac{d t}{t + 3} + \frac{b}{2} \int_{0}^{1} \frac{2 t + 2 x - 2 x}{t^{2} + 2 x t + x^{2} + 1} d t$ ${= a {[l n (t + 3)]}_{0}^{1} + \frac{b}{2} l n (t^{2} + 2 x t + x^{2} + 1)]}_{0}^{x} + c \int_{0}^{1} \frac{d t}{t^{2} + 2 x t + x^{2} + 1}$ $\int_{0}^{1} \frac{d t}{t^{2} + 2 x t + x^{2} + 1} = \int_{0}^{1} \frac{d t}{{(t + x)}^{2} + 1} =_{t + x = u} \int_{x}^{x + 1} \frac{d u}{1 + u^{2}}$ $= a r c t a n (x + 1) - a r c t a n x \Rightarrow$ $f^{^{'}} (x) = a {l n (\frac{4}{3})} + \frac{b}{2} (l n (4 x^{2} + 1) - l n (x^{2} + 1) + c (a r c t a n (x + 1) - a r c t a n x)$ $\Rightarrow f (x) = a l n (\frac{4}{3}) x + \frac{b}{2} \int l n (\frac{4 x^{2} + 1}{x^{2} + 1}) d x + c \int (a r c t a n (x + 1) - a r c t a n (x)) d x + c$ $. . . . b e c o n t i n u e d . . . .$
Commented by TawaTawa last updated on 01/Nov/19

$God bless you sir . Waiting for the rest sir$ $Thanks for your time sir .$
Commented by mathmax by abdo last updated on 01/Nov/19

$y o u a r e w e l c o m e .$
	Answered by mind is power last updated on 31/Oct/19
	$let u=tan^(−1) (x) ⇒x=tg(u)⇒dx=(1+tg^2 (u) )du ∫_2 ^3 ((tan^(−1) (x))/(1−x^2 ))dx=∫_(tan^− (2)) ^(tsn^− (3)) ((u.(1+tg^2 (u))du)/(1−tg^2 (u))) =∫−udu+2∫((udu)/(1−tg^2 (u))) −ln(u)+2∫((udu)/(1−(((e^(iu) −e^(−iu) )/(i(e^(iu) +e^(−iu) ))))^2 ))2∫((udu.)/(((e^(iu) +e^(−iu) )^2 +(e^(iu) −e^(−iu) )^2 )/((e^(iu) +e^(−iu) )^2 ))) =2∫((u(e^(2iu) +e^(−2iu) +2))/(2e^(2iu) +2e^(−2iu) ))du=∫udu+2∫((udu)/(e^(2iu) +e^(−2iu) )) =2∫((ue^(2iu) du)/(1+e^(4iu) ))=2∫((ue^(2iu) du)/((e^(2iu) +i)(e^(2iu) −i)))=∫((udu)/(e^(2iu) +i))+∫((udu)/(e^(2iu) −i)) =∫((udu)/((e^(iu) +e^(−i(π/4)) )(e^(iu) −e^((−iπ)/4) )))+∫((udu)/((e^(iu) +e^(i(π/4)) )(e^(iu) −e^((iπ)/4) ))) =(1/(2e^((−iπ)/4) )){∫((udu)/(e^(iu) −e^((−iπ)/4) ))−∫((udu)/(e^(iu) +e^((−iπ)/4) ))}+(1/(2e^((iπ)/4) )){∫((udu)/(e^(iu) −e^((iπ)/4) ))−∫((udu)/(e^(iu) +e^((iπ)/4) ))} =(e^(i(π/2)) /2){∫(u/(e^(i(u+(π/4))) −1))du}−(e^(−i(π/2)) /2){∫((udu)/(e^(i(u−((3π)/4))) −1))}+(e^(−i(π/2)) /2){∫((udu)/(e^(i(u−(π/4))) −1))}−(e^(i(π/2)) /2)∫((udu)/(e^(i(u+((3π)/4))) −1)) ∫_1 ^(1−z) ((ln(t))/(1−t))=Li_2 (z) ∫_(tan^− (2)) ^(tan^− (3)) ((udu)/(e^(i(u+c)) −1))du w=e^(i(u+c)) ⇒u=−iln(w)−c⇒du=((−idw)/w) ⇒∫_e^(i(tan^− (2)+c)) ^e^(i(tan^− (3)+c)) ((−iln(w)−c)/(w−1)).−i(dw/w) =∫((−ln(w)+ic)/(w(w−1)))=∫((−ln(w)+ic)/(w−1))+∫((ln(w))/w)dw−∫((icdw)/w) =−Li_2 (1−e^(i(tan^− (3)+c)) )+li_2 (1−e^(i(tan^(−2) +c)) )+iclog((e^(i(tan^− (3)+c)) /e^(i(tan^− (2)+c)) ))+log(((itan^− (3)+ic)/(itan^− (2)+ic)))−ic(itan^− (3)−itan^− (2)) put this for c=i(π/4),((−3iπ)/4),((−iπ)/4),((3iπ)/4)$
	$let u = \tan^{- 1} (x)$ $\Rightarrow x = tg (u) \Rightarrow dx = (1 + {tg}^{2} (u)) du$ $\int_{2}^{3} \frac{\tan^{- 1} (x)}{1 - x^{2}} d x = \int_{\tan^{-} (2)}^{{tsn}^{-} (3)} \frac{u . (1 + {tg}^{2} (u)) du}{1 - {tg}^{2} (u)}$ $= \int - udu + 2 \int \frac{udu}{1 - {tg}^{2} (u)}$ $- \ln (u) + 2 \int \frac{udu}{1 - {(\frac{e^{iu} - e^{- iu}}{i (e^{iu} + e^{- iu})})}^{2}} 2 \int \frac{udu .}{\frac{{(e^{iu} + e^{- iu})}^{2} + {(e^{iu} - e^{- iu})}^{2}}{{(e^{iu} + e^{- iu})}^{2}}}$ $= 2 \int \frac{u (e^{2 iu} + e^{- 2 iu} + 2)}{{2 e}^{2 iu} + {2 e}^{- 2 iu}} du = \int udu + 2 \int \frac{udu}{e^{2 iu} + e^{- 2 iu}}$ $= 2 \int \frac{{ue}^{2 iu} du}{1 + e^{4 iu}} = 2 \int \frac{{ue}^{2 iu} du}{(e^{2 iu} + i) (e^{2 iu} - i)} = \int \frac{udu}{e^{2 iu} + i} + \int \frac{udu}{e^{2 iu} - i}$ $= \int \frac{udu}{(e^{iu} + e^{- i \frac{π}{4}}) (e^{iu} - e^{\frac{- i π}{4}})} + \int \frac{udu}{(e^{iu} + e^{i \frac{π}{4}}) (e^{iu} - e^{\frac{i π}{4}})}$ $= \frac{1}{{2 e}^{\frac{- i π}{4}}} {\int \frac{udu}{e^{iu} - e^{\frac{- i π}{4}}} - \int \frac{udu}{e^{iu} + e^{\frac{- i π}{4}}}} + \frac{1}{{2 e}^{\frac{i π}{4}}} {\int \frac{udu}{e^{iu} - e^{\frac{i π}{4}}} - \int \frac{udu}{e^{iu} + e^{\frac{i π}{4}}}}$ $= \frac{e^{i \frac{π}{2}}}{2} {\int \frac{u}{e^{i (u + \frac{π}{4})} - 1} du} - \frac{e^{- i \frac{π}{2}}}{2} {\int \frac{udu}{e^{i (u - \frac{3 π}{4})} - 1}} + \frac{e^{- i \frac{π}{2}}}{2} {\int \frac{udu}{e^{i (u - \frac{π}{4})} - 1}} - \frac{e^{i \frac{π}{2}}}{2} \int \frac{udu}{e^{i (u + \frac{3 π}{4})} - 1}$ $\int_{1}^{1 - z} \frac{\ln (t)}{1 - t} = {Li}_{2} (z)$ $\int_{\tan^{-} (2)}^{\tan^{-} (3)} \frac{udu}{e^{i (u + c)} - 1} du$ $w = e^{i (u + c)} \Rightarrow u = - iln (w) - c \Rightarrow du = \frac{- idw}{w}$ $\Rightarrow \int_{e^{i (\tan^{-} (2) + c)}}^{e^{i (\tan^{-} (3) + c)}} \frac{- iln (w) - c}{w - 1} . - i \frac{dw}{w}$ $= \int \frac{- \ln (w) + ic}{w (w - 1)} = \int \frac{- \ln (w) + ic}{w - 1} + \int \frac{\ln (w)}{w} dw - \int \frac{icdw}{w}$ $= - {Li}_{2} (1 - e^{i (\tan^{-} (3) + c)}) + {li}_{2} (1 - e^{i (\tan^{- 2} + c)}) + iclog (\frac{e^{i (\tan^{-} (3) + c)}}{e^{i (\tan^{-} (2) + c)}}) + \log (\frac{{itan}^{-} (3) + ic}{{itan}^{-} (2) + ic}) - ic ({itan}^{-} (3) - {itan}^{-} (2))$ $put this for c = i \frac{π}{4}, \frac{- 3 i π}{4}, \frac{- i π}{4}, \frac{3 i π}{4}$
	Commented by TawaTawa last updated on 31/Oct/19

	$Wow, God bless you sir . I appreciate your time sir$
	Commented by mind is power last updated on 31/Oct/19

	$most Welcom$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum