
Question and Answers Forum
Question Number 72796 by Learner-123 last updated on 03/Nov/19
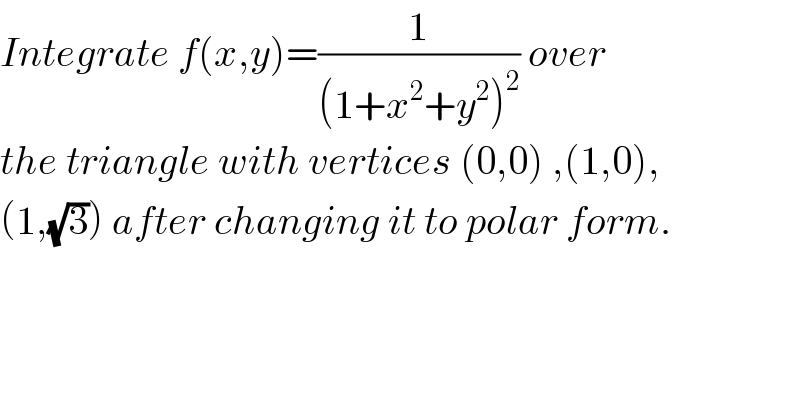
Answered by mind is power last updated on 03/Nov/19
![the triagle can bee expreced As={(x,y)∈IR^2 ∣ 0≤ y≤(√3)x,0≤x≤1} x=rcos(θ), y=rsin(θ) 0≤rsin(θ)≤rcos(θ)(√3) ⇒0≤tg(θ)≤(√3)....1 0≤rcos(θ)≤1⇒0≤r≤(1/(cos(θ)))...2 1⇒θ∈[0,(π/3)] ∫∫f(x,y)dx=∫_0 ^(π/3) .∫_0 ^(1/(cos(θ))) .((rdrdθ)/((1+r^2 )^2 ))=∫_0 ^(π/3) (∫_0 ^(1/(cos(θ))) (r/((1+r^2 )^2 )) )dθ =∫_0 ^(π/3) [−(1/2).(1/(1+r^2 ))]_0 ^(1/(cos(θ))) dθ=∫_0 ^(π/3) [−((cos^2 (θ))/(2(1+cos^2 (θ))))+(1/2)]dθ ∫_0 ^(π/3) ((dθ/(2(1+cos^2 (θ)))))=∫_0 ^(π/3) (((1+tg^2 (θ)))/(4+2tg^2 (θ)))dθ=(1/(2(√2)))∫_0 ^(π/3) .(((1/(√2))(1+tg^2 (θ)))/((1+(((tg(θ))/(√2)))^2 ))) =(1/(2(√2)))[arctan((√2)tg(θ))]_0 ^(π/3) =((arctan((√6)))/(2(√2)))](Q72802.png)
Commented by Learner-123 last updated on 03/Nov/19

Commented by mind is power last updated on 03/Nov/19

| ||
Question and Answers Forum | ||
Question Number 72796 by Learner-123 last updated on 03/Nov/19 | ||
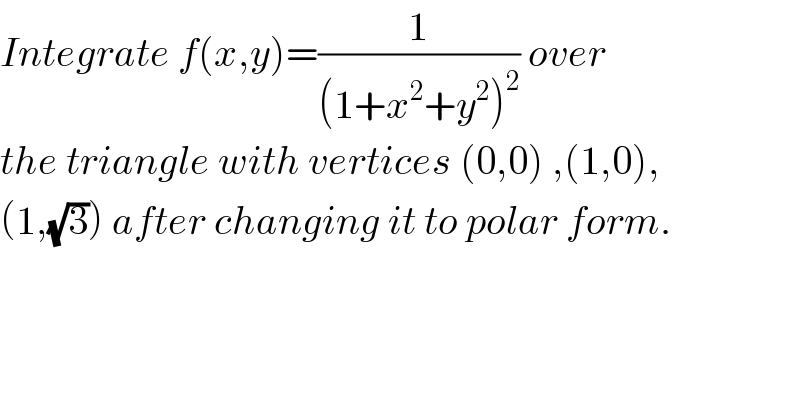 | ||
Answered by mind is power last updated on 03/Nov/19 | ||
![the triagle can bee expreced As={(x,y)∈IR^2 ∣ 0≤ y≤(√3)x,0≤x≤1} x=rcos(θ), y=rsin(θ) 0≤rsin(θ)≤rcos(θ)(√3) ⇒0≤tg(θ)≤(√3)....1 0≤rcos(θ)≤1⇒0≤r≤(1/(cos(θ)))...2 1⇒θ∈[0,(π/3)] ∫∫f(x,y)dx=∫_0 ^(π/3) .∫_0 ^(1/(cos(θ))) .((rdrdθ)/((1+r^2 )^2 ))=∫_0 ^(π/3) (∫_0 ^(1/(cos(θ))) (r/((1+r^2 )^2 )) )dθ =∫_0 ^(π/3) [−(1/2).(1/(1+r^2 ))]_0 ^(1/(cos(θ))) dθ=∫_0 ^(π/3) [−((cos^2 (θ))/(2(1+cos^2 (θ))))+(1/2)]dθ ∫_0 ^(π/3) ((dθ/(2(1+cos^2 (θ)))))=∫_0 ^(π/3) (((1+tg^2 (θ)))/(4+2tg^2 (θ)))dθ=(1/(2(√2)))∫_0 ^(π/3) .(((1/(√2))(1+tg^2 (θ)))/((1+(((tg(θ))/(√2)))^2 ))) =(1/(2(√2)))[arctan((√2)tg(θ))]_0 ^(π/3) =((arctan((√6)))/(2(√2)))](Q72802.png) | ||
| ||
Commented by Learner-123 last updated on 03/Nov/19 | ||
 | ||
Commented by mind is power last updated on 03/Nov/19 | ||
 | ||