Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 72908 by mathmax by abdo last updated on 04/Nov/19

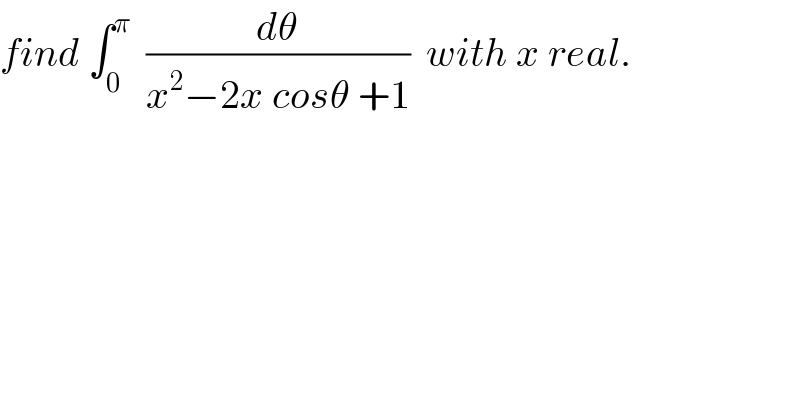
find ∫_0 ^π (dθ/(x^2 −2x cosθ +1)) with x real.

$${find}\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{d}\theta}{{x}^{\mathrm{2}} −\mathrm{2}{x}\:{cos}\theta\:+\mathrm{1}}\:\:{with}\:{x}\:{real}. \\ $$

Commented by mind is power last updated on 05/Nov/19

this is True for ∣x∣<1

$$\mathrm{this}\:\mathrm{is}\:\mathrm{True}\:\mathrm{for}\:\mid\mathrm{x}\mid<\mathrm{1} \\ $$

Commented by Tanmay chaudhury last updated on 05/Nov/19

Commented by Tanmay chaudhury last updated on 05/Nov/19

(1/(1−x^2 ))∫_0 ^π ((1−x^2 )/(x^2 −2xcosθ+1))dθ [when x<1 ] (1/(1−x^2 ))∫_0 ^π (1+2xcosθ+2x^2 cos2θ+2x^3 cos3θ+...)dθ (1/(1−x^2 ))[∣θ∣_0 ^π +others terms=0 =(π/(1−x^2 )) answer case−II when x>1 let k=(1/x) when x>1 so k<1 ∫_0 ^π (dθ/(x^2 −2xcosθ+1))dθ ∫_0 ^π (dθ/((1/k^2 )−(2/k)cosθ+1))dθ ∫_0 ^π ((k^2 dθ)/(1−2kcosθ+k^2 ))dθ [note k<1] k^2 ×(π/(1−k^2 )) =(π/((1/k^2 )−1))=so answer is =(π/(x^2 −1))

$$\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}−{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} −\mathrm{2}{xcos}\theta+\mathrm{1}}{d}\theta\:\:\:\left[{when}\:{x}<\mathrm{1}\:\:\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\pi} \left(\mathrm{1}+\mathrm{2}{xcos}\theta+\mathrm{2}{x}^{\mathrm{2}} {cos}\mathrm{2}\theta+\mathrm{2}{x}^{\mathrm{3}} {cos}\mathrm{3}\theta+...\right){d}\theta \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\left[\mid\theta\mid_{\mathrm{0}} ^{\pi} +{others}\:{terms}=\mathrm{0}\right. \\ $$$$=\frac{\pi}{\mathrm{1}−{x}^{\mathrm{2}} }\:{answer}\:\: \\ $$$${case}−{II}\:\:{when}\:{x}>\mathrm{1} \\ $$$${let}\:{k}=\frac{\mathrm{1}}{{x}}\:\:\:{when}\:{x}>\mathrm{1}\:\:\:{so}\:\:{k}<\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\pi} \frac{{d}\theta}{{x}^{\mathrm{2}} −\mathrm{2}{xcos}\theta+\mathrm{1}}{d}\theta \\ $$$$\int_{\mathrm{0}} ^{\pi} \frac{{d}\theta}{\frac{\mathrm{1}}{{k}^{\mathrm{2}} }−\frac{\mathrm{2}}{{k}}{cos}\theta+\mathrm{1}}{d}\theta \\ $$$$\int_{\mathrm{0}} ^{\pi} \frac{{k}^{\mathrm{2}} {d}\theta}{\mathrm{1}−\mathrm{2}{kcos}\theta+{k}^{\mathrm{2}} }{d}\theta\:\:\:\left[\boldsymbol{{note}}\:\boldsymbol{{k}}<\mathrm{1}\right] \\ $$$$\boldsymbol{{k}}^{\mathrm{2}} ×\frac{\pi}{\mathrm{1}−{k}^{\mathrm{2}} } \\ $$$$=\frac{\pi}{\frac{\mathrm{1}}{{k}^{\mathrm{2}} }−\mathrm{1}}=\boldsymbol{{so}}\:\boldsymbol{{answer}}\:\boldsymbol{{is}}\:\:\:=\frac{\pi}{{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 05/Nov/19

let f(x)=∫_0 ^π (dθ/(x^2 −2xcosθ +1)) changement tan((θ/2))=tgive f(x)=∫_0 ^∞ ((2dt)/((1+t^2 )(x^2 −2x((1−t^2 )/(1+t^2 )) +1))) =∫_0 ^∞ ((2dt)/(x^2 (1+t^2 )−2x(1−t^2 )+1+t^2 )) =∫_0 ^∞ ((2dt)/(x^2 +x^2 t^2 −2x+2xt^2 +1+t^2 )) =∫_0 ^∞ ((2dt)/((x^2 +2x+1)t^2 +x^2 −2x+1)) =∫_0 ^∞ ((2dt)/((x+1)^2 t^2 +(x−1)^2 )) =(1/((x+1)^2 ))∫_0 ^∞ ((2dt)/(t^2 +(((x−1)/(x+1)))^2 ))( if x≠−1 and x≠1) ⇒f(x)=_(t=∣((x−1)/(x+1))∣u) (1/((x+1)^2 ))∫_0 ^∞ (2/((((x−1)/(x+1)))^2 {1+u^2 }))∣((x−1)/(x+1))∣du =(1/((x−1)^2 ))×((∣x−1∣)/(∣x+1∣))∫_0 ^∞ ((2du)/(1+u^2 )) =(1/(∣x^2 −1∣))(2×(π/2))=(π/(∣x^2 −1∣)) ⇒ f(x)=(π/(∣x^2 −1∣))

$${let}\:{f}\left({x}\right)=\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{d}\theta}{{x}^{\mathrm{2}} −\mathrm{2}{xcos}\theta\:+\mathrm{1}}\:\:{changement}\:{tan}\left(\frac{\theta}{\mathrm{2}}\right)={tgive} \\ $$$${f}\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} −\mathrm{2}{x}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:+\mathrm{1}\right)}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{dt}}{{x}^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right)−\mathrm{2}{x}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)+\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{dt}}{{x}^{\mathrm{2}} \:+{x}^{\mathrm{2}} {t}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{2}{xt}^{\mathrm{2}} \:+\mathrm{1}+{t}^{\mathrm{2}} }\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{dt}}{\left({x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{1}\right){t}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{dt}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} {t}^{\mathrm{2}} +\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} \:+\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)^{\mathrm{2}} }\left(\:\:{if}\:{x}\neq−\mathrm{1}\:{and}\:\right. \\ $$$$\left.{x}\neq\mathrm{1}\right)\:\Rightarrow{f}\left({x}\right)=_{{t}=\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid{u}} \:\:\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2}}{\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)^{\mathrm{2}} \left\{\mathrm{1}+{u}^{\mathrm{2}} \right\}}\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\mid{du} \\ $$$$=\frac{\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }×\frac{\mid{x}−\mathrm{1}\mid}{\mid{x}+\mathrm{1}\mid}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mid{x}^{\mathrm{2}} −\mathrm{1}\mid}\left(\mathrm{2}×\frac{\pi}{\mathrm{2}}\right)=\frac{\pi}{\mid{x}^{\mathrm{2}} −\mathrm{1}\mid}\:\Rightarrow \\ $$$${f}\left({x}\right)=\frac{\pi}{\mid{x}^{\mathrm{2}} −\mathrm{1}\mid} \\ $$

Commented by Tanmay chaudhury last updated on 05/Nov/19

whom you target by this remarks...reply now

$${whom}\:{you}\:{target}\:{by}\:{this}\:{remarks}...{reply}\:{now} \\ $$

Commented by ajfour last updated on 05/Nov/19

Great method, Tanmay Sir..

$${Great}\:{method},\:{Tanmay}\:{Sir}.. \\ $$

Commented by Tanmay chaudhury last updated on 05/Nov/19

Thank you sir...

$${Thank}\:{you}\:{sir}... \\ $$

Commented by ajfour last updated on 05/Nov/19

sorry sir, i concluded this on a fleeting glance, forgive me..

$${sorry}\:{sir},\:{i}\:{concluded}\:{this}\:{on}\:{a} \\ $$$${fleeting}\:{glance},\:{forgive}\:{me}.. \\ $$

Commented by Tanmay chaudhury last updated on 05/Nov/19

Commented by Tanmay chaudhury last updated on 05/Nov/19

taken from SL loney

$${taken}\:{from}\:{SL}\:{loney} \\ $$

Commented by Tanmay chaudhury last updated on 05/Nov/19

taken from ML khanna

$${taken}\:{from}\:{ML}\:{khanna} \\ $$

Commented by Tanmay chaudhury last updated on 05/Nov/19

Commented by Tanmay chaudhury last updated on 05/Nov/19

sir pls check i have considerd both case x<1 and x>1 pls

$${sir}\:{pls}\:{check}\:{i}\:{have}\:{considerd}\:\:{both}\:{case} \\ $$$${x}<\mathrm{1}\:\:\:\:{and}\:\:{x}>\mathrm{1}\:\:{pls} \\ $$

Commented by mind is power last updated on 05/Nov/19

nice solution

$$\mathrm{nice}\:\mathrm{solution}\:\: \\ $$

Commented by mind is power last updated on 05/Nov/19

nice sir

$$\mathrm{nice}\:\mathrm{sir}\: \\ $$

Answered by mind is power last updated on 05/Nov/19

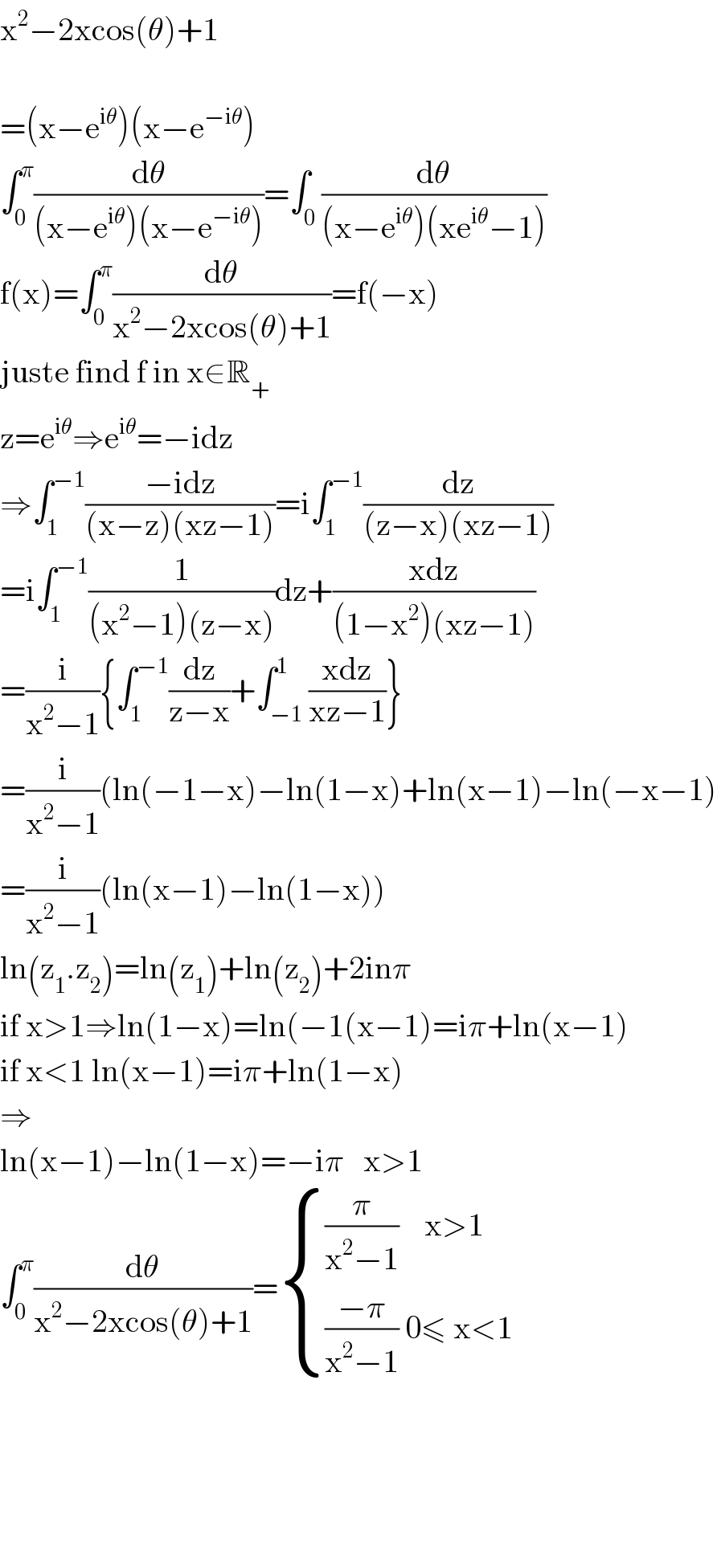
x^2 −2xcos(θ)+1 =(x−e^(iθ) )(x−e^(−iθ) ) ∫_0 ^π (dθ/((x−e^(iθ) )(x−e^(−iθ) )))=∫_0 (dθ/((x−e^(iθ) )(xe^(iθ) −1))) f(x)=∫_0 ^π (dθ/(x^2 −2xcos(θ)+1))=f(−x) juste find f in x∈R_+ z=e^(iθ) ⇒e^(iθ) =−idz ⇒∫_1 ^(−1) ((−idz)/((x−z)(xz−1)))=i∫_1 ^(−1) (dz/((z−x)(xz−1))) =i∫_1 ^(−1) (1/((x^2 −1)(z−x)))dz+((xdz)/((1−x^2 )(xz−1))) =(i/(x^2 −1)){∫_1 ^(−1) (dz/(z−x))+∫_(−1) ^1 ((xdz)/(xz−1))} =(i/(x^2 −1))(ln(−1−x)−ln(1−x)+ln(x−1)−ln(−x−1) =(i/(x^2 −1))(ln(x−1)−ln(1−x)) ln(z_1 .z_2 )=ln(z_1 )+ln(z_2 )+2inπ if x>1⇒ln(1−x)=ln(−1(x−1)=iπ+ln(x−1) if x<1 ln(x−1)=iπ+ln(1−x) ⇒ ln(x−1)−ln(1−x)=−iπ x>1 ∫_0 ^π (dθ/(x^2 −2xcos(θ)+1))= { (((π/(x^2 −1)) x>1)),((((−π)/(x^2 −1)) 0≤ x<1)) :}

$$\mathrm{x}^{\mathrm{2}} −\mathrm{2xcos}\left(\theta\right)+\mathrm{1} \\ $$$$ \\ $$$$=\left(\mathrm{x}−\mathrm{e}^{\mathrm{i}\theta} \right)\left(\mathrm{x}−\mathrm{e}^{−\mathrm{i}\theta} \right) \\ $$$$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{d}\theta}{\left(\mathrm{x}−\mathrm{e}^{\mathrm{i}\theta} \right)\left(\mathrm{x}−\mathrm{e}^{−\mathrm{i}\theta} \right)}=\int_{\mathrm{0}} \frac{\mathrm{d}\theta}{\left(\mathrm{x}−\mathrm{e}^{\mathrm{i}\theta} \right)\left(\mathrm{xe}^{\mathrm{i}\theta} −\mathrm{1}\right)} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{d}\theta}{\mathrm{x}^{\mathrm{2}} −\mathrm{2xcos}\left(\theta\right)+\mathrm{1}}=\mathrm{f}\left(−\mathrm{x}\right) \\ $$$$\mathrm{juste}\:\mathrm{find}\:\mathrm{f}\:\mathrm{in}\:\mathrm{x}\in\mathbb{R}_{+} \\ $$$$\mathrm{z}=\mathrm{e}^{\mathrm{i}\theta} \Rightarrow\mathrm{e}^{\mathrm{i}\theta} =−\mathrm{idz} \\ $$$$\Rightarrow\int_{\mathrm{1}} ^{−\mathrm{1}} \frac{−\mathrm{idz}}{\left(\mathrm{x}−\mathrm{z}\right)\left(\mathrm{xz}−\mathrm{1}\right)}=\mathrm{i}\int_{\mathrm{1}} ^{−\mathrm{1}} \frac{\mathrm{dz}}{\left(\mathrm{z}−\mathrm{x}\right)\left(\mathrm{xz}−\mathrm{1}\right)} \\ $$$$=\mathrm{i}\int_{\mathrm{1}} ^{−\mathrm{1}} \frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{z}−\mathrm{x}\right)}\mathrm{dz}+\frac{\mathrm{xdz}}{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{xz}−\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{i}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\left\{\int_{\mathrm{1}} ^{−\mathrm{1}} \frac{\mathrm{dz}}{\mathrm{z}−\mathrm{x}}+\int_{−\mathrm{1}} ^{\mathrm{1}} \frac{\mathrm{xdz}}{\mathrm{xz}−\mathrm{1}}\right\} \\ $$$$=\frac{\mathrm{i}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\left(\mathrm{ln}\left(−\mathrm{1}−\mathrm{x}\right)−\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)+\mathrm{ln}\left(\mathrm{x}−\mathrm{1}\right)−\mathrm{ln}\left(−\mathrm{x}−\mathrm{1}\right)\right. \\ $$$$=\frac{\mathrm{i}}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\left(\mathrm{ln}\left(\mathrm{x}−\mathrm{1}\right)−\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\right) \\ $$$$\mathrm{ln}\left(\mathrm{z}_{\mathrm{1}} .\mathrm{z}_{\mathrm{2}} \right)=\mathrm{ln}\left(\mathrm{z}_{\mathrm{1}} \right)+\mathrm{ln}\left(\mathrm{z}_{\mathrm{2}} \right)+\mathrm{2in}\pi \\ $$$$\mathrm{if}\:\mathrm{x}>\mathrm{1}\Rightarrow\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)=\mathrm{ln}\left(−\mathrm{1}\left(\mathrm{x}−\mathrm{1}\right)=\mathrm{i}\pi+\mathrm{ln}\left(\mathrm{x}−\mathrm{1}\right)\right. \\ $$$$\mathrm{if}\:\mathrm{x}<\mathrm{1}\:\mathrm{ln}\left(\mathrm{x}−\mathrm{1}\right)=\mathrm{i}\pi+\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right) \\ $$$$\Rightarrow \\ $$$$\mathrm{ln}\left(\mathrm{x}−\mathrm{1}\right)−\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)=−\mathrm{i}\pi\:\:\:\mathrm{x}>\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{d}\theta}{\mathrm{x}^{\mathrm{2}} −\mathrm{2xcos}\left(\theta\right)+\mathrm{1}}=\begin{cases}{\frac{\pi}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:\:\:\:\mathrm{x}>\mathrm{1}}\\{\frac{−\pi}{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\:\mathrm{0}\leqslant\:\mathrm{x}<\mathrm{1}}\end{cases} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Answered by ajfour last updated on 05/Nov/19

I=∫_0 ^( π) (dθ/((x−1)^2 +4xsin^2 (θ/2))) dividing by cos^2 (θ/2) and let tan (θ/2)=t ⇒ (1/2)sec^2 (θ/2)dθ=dt ⇒ (sec^2 (θ/2))dθ=2dt I=∫^ ((2dt)/((x−1)^2 (1+t^2 )+4xt^2 )) =(1/((x+1)^2 ))∫((2dt)/(t^2 +(((x−1)/(x+1)))^2 ))=(2/(x^2 −1))tan^(−1) [((t(x+1))/(x−1))]+c =(2/(x^2 −1))((π/2)) = (π/(x^2 −1)) . I = (π/(x^2 −1)) ∙

$${I}=\int_{\mathrm{0}} ^{\:\pi} \frac{{d}\theta}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{4}{x}\mathrm{sin}\:^{\mathrm{2}} \frac{\theta}{\mathrm{2}}} \\ $$$${dividing}\:{by}\:\mathrm{cos}\:^{\mathrm{2}} \frac{\theta}{\mathrm{2}}\:\:\:\:{and} \\ $$$$\:\:{let}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}={t}\:\:\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:^{\mathrm{2}} \frac{\theta}{\mathrm{2}}{d}\theta={dt} \\ $$$$\Rightarrow\:\:\left(\mathrm{sec}\:^{\mathrm{2}} \frac{\theta}{\mathrm{2}}\right){d}\theta=\mathrm{2}{dt} \\ $$$${I}=\int^{\:} \frac{\mathrm{2}{dt}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right)+\mathrm{4}{xt}^{\mathrm{2}} } \\ $$$$\:\:=\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\int\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\left(\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\right)^{\mathrm{2}} }=\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{1}}\mathrm{tan}^{−\mathrm{1}} \left[\frac{{t}\left({x}+\mathrm{1}\right)}{{x}−\mathrm{1}}\right]+{c} \\ $$$$\:=\frac{\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{1}}\left(\frac{\pi}{\mathrm{2}}\right)\:=\:\frac{\pi}{{x}^{\mathrm{2}} −\mathrm{1}}\:. \\ $$$$\:{I}\:=\:\frac{\pi}{{x}^{\mathrm{2}} −\mathrm{1}}\:\centerdot \\ $$

Commented by mind is power last updated on 05/Nov/19

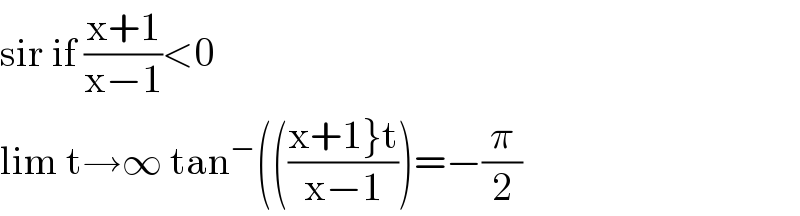
sir if ((x+1)/(x−1))<0 lim t→∞ tan^− ((((x+1}t)/(x−1)))=−(π/2)

$$\mathrm{sir}\:\mathrm{if}\:\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}<\mathrm{0} \\ $$$$\mathrm{lim}\:\mathrm{t}\rightarrow\infty\:\mathrm{tan}^{−} \left(\left(\frac{\left.\mathrm{x}+\mathrm{1}\right\}\mathrm{t}}{\mathrm{x}−\mathrm{1}}\right)=−\frac{\pi}{\mathrm{2}}\right. \\ $$

Commented by ajfour last updated on 05/Nov/19

true, thanks for the light.

$${true},\:{thanks}\:{for}\:{the}\:{light}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com