let P_n (x)=(x+1)^n −(x−1)^n 1) fartorize inside C(x) P_n (x) 2)calculate Π


Question and Answers Forum

All Questions Topic List
Relation and Functions Questions
Previous in All Question Next in All Question
Previous in Relation and Functions Next in Relation and Functions
Question Number 73059 by mathmax by abdo last updated on 05/Nov/19

$l e t P_{n} (x) = {(x + 1)}^{n} - {(x - 1)}^{n}$ $1) f a r t o r i z e i n s i d e C (x) P_{n} (x)$ $2) c a l c u l a t e \prod_{k = 1}^{p} c o t a n (\frac{k π}{2 p + 1})$
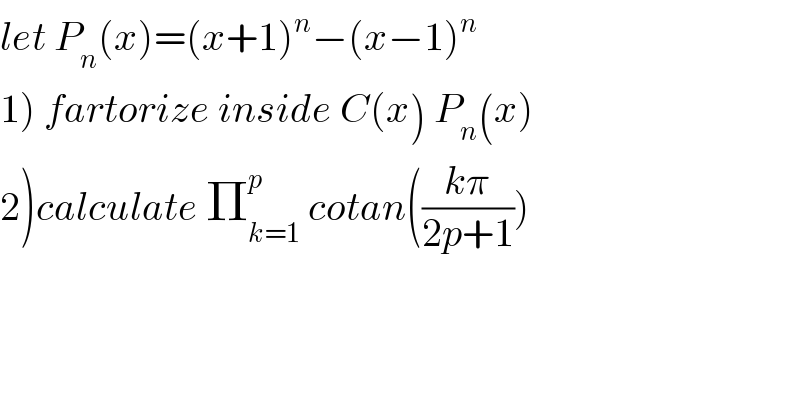
Commented by mathmax by abdo last updated on 06/Nov/19
$1) P_n (x)=0 ⇔(x+1)^n =(x−1)^n ⇔(((x−1)/(x+1)))^n =1 let z=((x−1)/(x+1)) (e) ⇒z^n =1 ⇒z^n =e^(i2kπ) ⇒z_k =e^((i2kπ)/n) and k∈[[0,n−1]] z=((x−1)/(x+1)) ⇒zx+z =x−1 ⇒(z−1)x=−z−1 ⇒x=((1+z)/(1−z)) ⇒ the roots of P_n (x)=0 are x_k =((1+z_k )/(1−z_k )) =((1+e^((i2kπ)/n) )/(1−e^((i2kπ)/n) )) =((1+cos(((2kπ)/n))+isin(((2kπ)/n)))/(1−cos(((2kπ)/n))−isin(((2kπ)/n)))) =((2cos^2 (((kπ)/n))+2isin(((kπ)/n))cos(((kπ)/n)))/(2sin^2 (((kπ)/n))−2isin(((kπ)/n))cos(((kπ)/n)))) =((cos(((kπ)/n))e^(i((kπ)/n)) )/(−isin(((kπ)/n))e^((ikπ)/n) )) =i cotan(((kπ)/n)) ⇒x_k =i cotan(((kπ)/n)) with k∈[[1,n−1]] and P_n (x)=aΠ_(k=1) ^(n−1) (x−icotan(((kπ)/n))) letfind a we have P_n (x)=Σ_(k=0) ^n C_n ^k x^k −Σ_(k=0) ^n C_n ^k x^k (−1)^(n−k) =Σ_(k=0) ^n { 1−(−1)^(n−k) }C_n ^k x^k ⇒a =2 C_n ^(n−1) =2n ⇒ P_n (x)=2nΠ_(k=1) ^(n−1) (x−i cotan(((kπ)/n))) ⇒P_(2n+1) (x) =2(2n+1)Π_(k=1) ^(2n) (x−icotan(((kπ)/(2n+1)))) ⇒ P_(2n+1) (0) =2(2n+1)Π_(k=1) ^(2n) (−icotan(((kπ)/(2n+1)))) =2(2n+1)(−i)^(2n) Π_(k=1) ^(2n) cotan(((kπ)/(2n+1))) and P_n (0)=1−(−1)^n ⇒P_(2n+1) (0) =2 ⇒(2n+1)(−1)^n Π_(k=1) ^(2n) cotan(((kπ)/(2n+1)))=1 ⇒ (−1)^n Π_(k=1) ^(2n) cotan(((kπ)/(2n+1)))=(1/(2n+1)) we have Π_(k=1) ^(2n) cotan(((kπ)/(2n+1)))=Π_(k=1) ^n cotan(((kπ)/(2n+1)))Π_(k=n+1) ^(2n) cotan(((kπ)/(2n+1))) =_(k−n=p) Π_(k=1) ^n cotan(((kπ)/(2n+1)))×Π_(p=1) ^n cotan((((n+p)π)/(2n+1))) rest to prove thst Π_(p=1) ^n cotan((((n+p)π)/(2n+1)))=(−1)^n Π_(p=1) ^(n ) cotan(((pπ)/(2n+1))) ⇒(Π_(k=1) ^n cotan(((kπ)/(2n+1))))^2 =(1/(2n+1)) ⇒Π_(k=1) ^n cotan(((kπ)/(2n+1)))=(1/(√(2n+1)))$
$1) P_{n} (x) = 0 \Leftrightarrow {(x + 1)}^{n} = {(x - 1)}^{n} \Leftrightarrow {(\frac{x - 1}{x + 1})}^{n} = 1 l e t z = \frac{x - 1}{x + 1}$ $(e) \Rightarrow z^{n} = 1 \Rightarrow z^{n} = e^{i 2 k π} \Rightarrow z_{k} = e^{\frac{i 2 k π}{n}} a n d k \in [[0, n - 1]]$ $z = \frac{x - 1}{x + 1} \Rightarrow z x + z = x - 1 \Rightarrow (z - 1) x = - z - 1 \Rightarrow x = \frac{1 + z}{1 - z} \Rightarrow$ $t h e r o o t s o f P_{n} (x) = 0 a r e x_{k} = \frac{1 + z_{k}}{1 - z_{k}} = \frac{1 + e^{\frac{i 2 k π}{n}}}{1 - e^{\frac{i 2 k π}{n}}}$ $= \frac{1 + c o s (\frac{2 k π}{n}) + i s i n (\frac{2 k π}{n})}{1 - c o s (\frac{2 k π}{n}) - i s i n (\frac{2 k π}{n})} = \frac{2 {c o s}^{2} (\frac{k π}{n}) + 2 i s i n (\frac{k π}{n}) c o s (\frac{k π}{n})}{2 {s i n}^{2} (\frac{k π}{n}) - 2 i s i n (\frac{k π}{n}) c o s (\frac{k π}{n})}$ $= \frac{c o s (\frac{k π}{n}) e^{i \frac{k π}{n}}}{- i s i n (\frac{k π}{n}) e^{\frac{i k π}{n}}} = i c o t a n (\frac{k π}{n}) \Rightarrow x_{k} = i c o t a n (\frac{k π}{n})$ $w i t h k \in [[1, n - 1]] a n d P_{n} (x) = a \prod_{k = 1}^{n - 1} (x - i c o t a n (\frac{k π}{n}))$ $l e t f i n d a w e h a v e P_{n} (x) = \sum_{k = 0}^{n} C_{n}^{k} x^{k} - \sum_{k = 0}^{n} C_{n}^{k} x^{k} {(- 1)}^{n - k}$ $= \sum_{k = 0}^{n} {1 - {(- 1)}^{n - k}} C_{n}^{k} x^{k} \Rightarrow a = 2 C_{n}^{n - 1} = 2 n \Rightarrow$ $P_{n} (x) = 2 n \prod_{k = 1}^{n - 1} (x - i c o t a n (\frac{k π}{n}))$ $\Rightarrow P_{2 n + 1} (x) = 2 (2 n + 1) \prod_{k = 1}^{2 n} (x - i c o t a n (\frac{k π}{2 n + 1})) \Rightarrow$ $P_{2 n + 1} (0) = 2 (2 n + 1) \prod_{k = 1}^{2 n} (- i c o t a n (\frac{k π}{2 n + 1}))$ $= 2 (2 n + 1) {(- i)}^{2 n} \prod_{k = 1}^{2 n} c o t a n (\frac{k π}{2 n + 1}) a n d P_{n} (0) = 1 - {(- 1)}^{n}$ $\Rightarrow P_{2 n + 1} (0) = 2 \Rightarrow (2 n + 1) {(- 1)}^{n} \prod_{k = 1}^{2 n} c o t a n (\frac{k π}{2 n + 1}) = 1 \Rightarrow$ ${(- 1)}^{n} \prod_{k = 1}^{2 n} c o t a n (\frac{k π}{2 n + 1}) = \frac{1}{2 n + 1} w e h a v e$ $\prod_{k = 1}^{2 n} c o t a n (\frac{k π}{2 n + 1}) = \prod_{k = 1}^{n} c o t a n (\frac{k π}{2 n + 1}) \prod_{k = n + 1}^{2 n} c o t a n (\frac{k π}{2 n + 1})$ $=_{k - n = p} \prod_{k = 1}^{n} c o t a n (\frac{k π}{2 n + 1}) \times \prod_{p = 1}^{n} c o t a n (\frac{(n + p) π}{2 n + 1})$ $r e s t t o p r o v e t h s t \prod_{p = 1}^{n} c o t a n (\frac{(n + p) π}{2 n + 1}) = {(- 1)}^{n} \prod_{p = 1}^{n} c o t a n (\frac{p π}{2 n + 1})$ $\Rightarrow {(\prod_{k = 1}^{n} c o t a n (\frac{k π}{2 n + 1}))}^{2} = \frac{1}{2 n + 1} \Rightarrow \prod_{k = 1}^{n} c o t a n (\frac{k π}{2 n + 1}) = \frac{1}{\sqrt{2 n + 1}}$
Commented by mind is power last updated on 06/Nov/19

$nice$
Commented by mathmax by abdo last updated on 06/Nov/19

$t h a n k s s i r .$
	Answered by mind is power last updated on 06/Nov/19
	$p_n (x)=0⇒((x+1)/(x−1))=e^((2ikπ)/n) ,k≤n ⇒x(1−e^((2ikπ)/n) )=−e^((2ikπ)/n) −1 ⇒k≠0 x=((e^((2ikπ)/n) +1)/(e^((2ikπ)/n) −1))=((e^(i((kπ)/n)) (2cos(((kπ)/n))))/(e^(i((kπ)/n)) (2isin(((kπ)/n)))))=−icot(((kπ)/n)) p_n (x)=aΠ_(k=1) ^(n−1) (x+icot(((kπ)/n)) let n=2p+1 p_n (x)=Π_(k=1) ^(2p) (x+icot(((kπ)/(2p+1)))) =Π_(k=1) ^p (x+icot(((kπ)/(2p+1)))).Π_(k=p+1) ^(2p) (x+icot(((kπ)/(2p+1))) =Π_(k=1) ^p (x+icot(((kπ)/(2p+1)))).Π_(k=0) ^(p−1) (x+icot(((2p−k)π)/(2p+1)))) =Π_(k=1) ^p (x+icot(((kπ)/(2p+1))))Π_(k=0) ^(p−1) (x−icot(((k+1)/(2p+1)))π)=(1+x)^n −(x−1)^n pour x=0 onaΠ_(k=1) ^p (icot(((kπ)/(2p+1))))(Π_(k=1) ^p −icot(((kπ)/(2p+1))))= ⇒{Π_(k=1) ^p cot(((kπ)/(2p+1)))}^2 =(2/a) ⇒Π_(k=1) ^p cot(((kπ)/(2p+1)))=(√(2/a))=(1/(√(2p+1))) a=2C_n ^1 =2n=4p+2 cause ∀k∈[1,n] 0< ((kπ)/(2p+1))<(π/2)⇒cot(((kπ)/(2p+1)))>0$
	$p_{n} (x) = 0 \Rightarrow \frac{x + 1}{x - 1} = e^{\frac{2 ik π}{n}}, k ⩽ n$ $\Rightarrow x (1 - e^{\frac{2 ik π}{n}}) = - e^{\frac{2 ik π}{n}} - 1$ $\Rightarrow k \neq 0$ $x = \frac{e^{\frac{2 ik π}{n}} + 1}{e^{\frac{2 ik π}{n}} - 1} = \frac{e^{i \frac{k π}{n}} (2 \cos (\frac{k π}{n}))}{e^{i \frac{k π}{n}} (2 isin (\frac{k π}{n}))} = - icot (\frac{k π}{n})$ $p_{n} (x) = a \underset{k = 1}{\prod^{n - 1}} (x + icot (\frac{k π}{n})$ $let n = 2 p + 1$ $p_{n} (x) = \underset{k = 1}{\prod^{2 p}} (x + icot (\frac{k π}{2 p + 1}))$ $= \underset{k = 1}{\prod^{p}} (x + icot (\frac{k π}{2 p + 1})) . \underset{k = p + 1}{\prod^{2 p}} (x + icot (\frac{k π}{2 p + 1})$ $= \underset{k = 1}{\prod^{p}} (x + icot (\frac{k π}{2 p + 1})) . \underset{k = 0}{\prod^{p - 1}} (x + icot (\frac{2 p - k) π}{2 p + 1}))$ $= \underset{k = 1}{\prod^{p}} (x + icot (\frac{k π}{2 p + 1})) \underset{k = 0}{\prod^{p - 1}} (x - icot (\frac{k + 1}{2 p + 1}) π) = {(1 + x)}^{n} - {(x - 1)}^{n}$ $pour x = 0$ $ona \underset{k = 1}{\prod^{p}} (icot (\frac{k π}{2 p + 1})) (\underset{k = 1}{\prod^{p}} - icot (\frac{k π}{2 p + 1})) =$ $\Rightarrow {\underset{k = 1}{\prod^{p}} \cot (\frac{k π}{2 p + 1})}^{2} = \frac{2}{a}$ $\Rightarrow \underset{k = 1}{\prod^{p}} \cot (\frac{k π}{2 p + 1}) = \sqrt{\frac{2}{a}} = \frac{1}{\sqrt{2 p + 1}}$ $a = {2 C}_{n}^{1} = 2 n = 4 p + 2$ $cause \forall k \in [1, n] 0 < \frac{k π}{2 p + 1} < \frac{π}{2} \Rightarrow \cot (\frac{k π}{2 p + 1}) > 0$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum