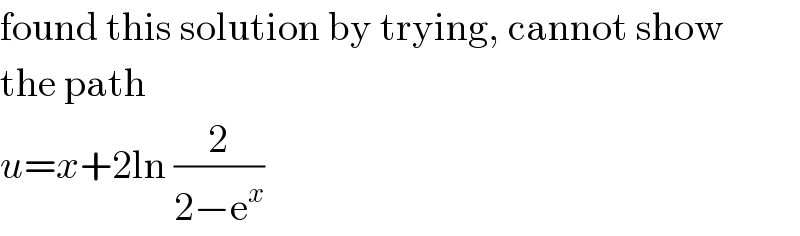Question and Answers Forum
Previous in Differential Equation Next in Differential Equation
Question Number 73080 by oyemi kemewari last updated on 06/Nov/19
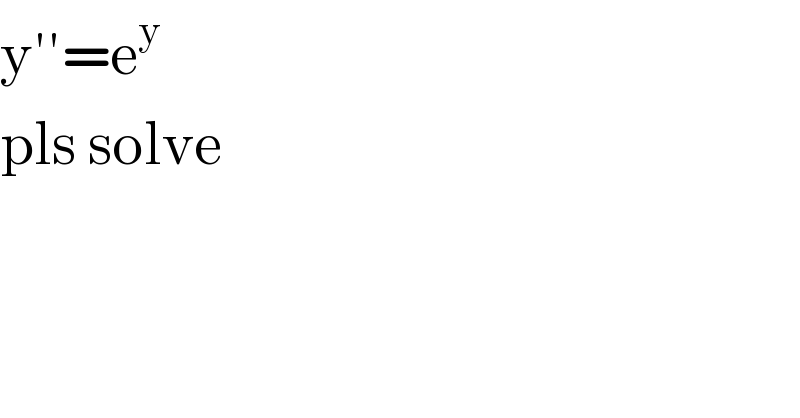
Answered by mind is power last updated on 06/Nov/19
/(−2(√(−c))))π_ −b,((2kπ)/(−2(√(−c))))−b[ for a given integer k](Q73086.png)
Commented by oyemi kemewari last updated on 06/Nov/19
thanks so much
Commented by mind is power last updated on 06/Nov/19

Commented by MJS last updated on 06/Nov/19