
Previous in Relation and Functions Next in Relation and Functions
Question Number 7317 by lakshaysethi last updated on 24/Aug/16
![Prove that [((n+1)/2)]+[((n+2)/4)]+[((n+4)/8)]+[((n+8)/( 16))]+........=n. Such that [.] denotes greatest integer function and n∈N.](Q7317.png)
$${Prove}\:{that}\:\left[\frac{{n}+\mathrm{1}}{\mathrm{2}}\right]+\left[\frac{{n}+\mathrm{2}}{\mathrm{4}}\right]+\left[\frac{{n}+\mathrm{4}}{\mathrm{8}}\right]+\left[\frac{{n}+\mathrm{8}}{\:\mathrm{16}}\right]+........={n}. \\ $$$${Such}\:{that}\:\left[.\right]\:{denotes}\:{greatest}\:{integer}\:{function}\:{and}\:{n}\in{N}. \\ $$
Commented by FilupSmith last updated on 23/Aug/16

$${S}=\underset{{t}=\mathrm{1}} {\overset{\infty} {\sum}}\lceil\frac{{n}+\mathrm{2}^{{t}−\mathrm{1}} }{\mathrm{2}^{{t}} }\rceil \\ $$$${S}=\underset{{t}=\mathrm{1}} {\overset{\infty} {\sum}}\lceil\frac{{n}}{\mathrm{2}^{{t}} }+\frac{\mathrm{1}}{\mathrm{2}}\rceil \\ $$$$\mathrm{if}\:\:{n}\geqslant\mathrm{2}^{{t}} \:\:\:\Rightarrow\:\:\:\frac{{n}}{\mathrm{2}^{{t}} }\geqslant\mathrm{1} \\ $$$$\therefore\lceil\frac{{n}}{\mathrm{2}^{{t}} }+\frac{\mathrm{1}}{\mathrm{2}}\rceil\geqslant\mathrm{2} \\ $$$$\mathrm{if}\:\:{n}\leqslant\mathrm{2}^{{t}} \:\:\:\Rightarrow\:\:\:\frac{{n}}{\mathrm{2}^{{t}} }\leqslant\mathrm{1} \\ $$$$\therefore\lceil\frac{{n}}{\mathrm{2}^{{t}} }+\frac{\mathrm{1}}{\mathrm{2}}\rceil=\mathrm{1}\vee\mathrm{2} \\ $$$$ \\ $$$$\therefore\:\mathrm{sequence}\:\mathrm{is}: \\ $$$$\mathrm{2}+\mathrm{2}+...+\mathrm{1}+\mathrm{1}+\mathrm{1}+...+\mathrm{0}\:\:\:\left(\mathrm{0}\:{when}\:{t}=\infty\right) \\ $$$$\therefore{S}=\infty \\ $$$$ \\ $$$$\therefore\lceil\frac{{n}+\mathrm{2}}{\mathrm{4}}\rceil+\lceil\frac{{n}+\mathrm{4}}{\mathrm{6}}\rceil+\lceil\frac{{n}+\mathrm{8}}{\mathrm{16}}\rceil+...={n}\:\:\:\:\mathrm{is}\:\mathrm{false} \\ $$$$\mathrm{this}\:\mathrm{is}\:\mathrm{because}\:\mathrm{for}\:\frac{{n}+\mathrm{2}^{{t}} }{\mathrm{2}^{{t}+\mathrm{1}} }>\mathrm{1},\:\lceil\frac{{n}+\mathrm{2}^{{t}} }{\mathrm{2}^{{t}+\mathrm{1}} }\rceil\geqslant\mathrm{1} \\ $$$${therefore}\:{no}\:{solution}\:{exists}\:{for}\:{n}\in{N} \\ $$
Commented by prakash jain last updated on 23/Aug/16
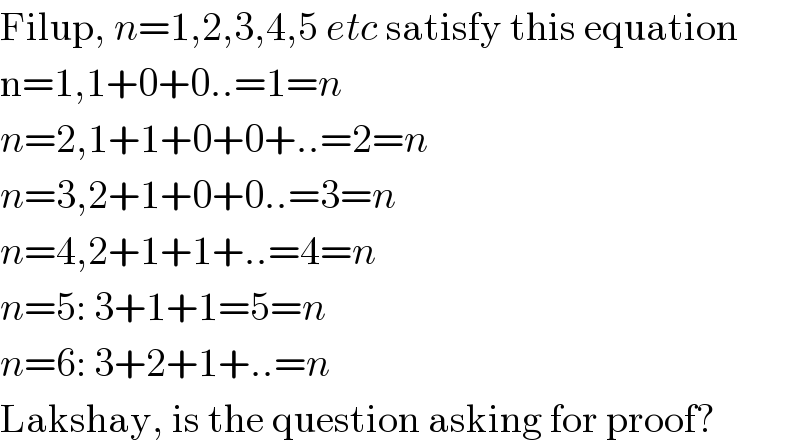
$$\mathrm{Filup},\:{n}=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5}\:{etc}\:\mathrm{satisfy}\:\mathrm{this}\:\mathrm{equation} \\ $$$$\mathrm{n}=\mathrm{1},\mathrm{1}+\mathrm{0}+\mathrm{0}..=\mathrm{1}={n} \\ $$$${n}=\mathrm{2},\mathrm{1}+\mathrm{1}+\mathrm{0}+\mathrm{0}+..=\mathrm{2}={n} \\ $$$${n}=\mathrm{3},\mathrm{2}+\mathrm{1}+\mathrm{0}+\mathrm{0}..=\mathrm{3}={n} \\ $$$${n}=\mathrm{4},\mathrm{2}+\mathrm{1}+\mathrm{1}+..=\mathrm{4}={n} \\ $$$${n}=\mathrm{5}:\:\mathrm{3}+\mathrm{1}+\mathrm{1}=\mathrm{5}={n} \\ $$$${n}=\mathrm{6}:\:\mathrm{3}+\mathrm{2}+\mathrm{1}+..={n} \\ $$$$\mathrm{Lakshay},\:\mathrm{is}\:\mathrm{the}\:\mathrm{question}\:\mathrm{asking}\:\mathrm{for}\:\mathrm{proof}? \\ $$
Commented by Yozzia last updated on 24/Aug/16
![[(n/2)+(1/2)]+[(n/4)+(1/2)]+[(n/8)+(1/2)]+[(n/(16))+(1/2)]+...+[(n/2^k )+(1/2)]=S_k Any integer can be represented in base 2 according to the base representation theorem. ∴ n=Σ_(i=0) ^m a_i 2^i where each a_i =0 ∨ 1. ∴ (n/2^k )+(1/2)=(1/2)+Σ_(i=0) ^m a_i 2^(i−k) . Now, for k,m∈N, k<m or k=m or k>m. If k<m then for some i∈Z^≥ , i−k<0 or i<k⇒i≤k−1. Hence we can write (n/2^k )+(1/2)=R+a_k 2^(k−k) +a_(k+1) 2^((k+1)−k) +a_(k+2) 2^((k+2)−k) +...+a_(m−1) 2^((m−1)−k) +a_m 2^(m−k) (n/2^k )+(1/2)=R+a_k +a_(k+1) 2+a_(k+2) 2^2 +...+a_(m−1) 2^((m−1)−k) +a_m 2^(m−k) where R=2^(−1) +a_0 2^(0−k) +a_1 2^(1−k) +a_2 2^(2−k) +a_3 2^(3−k) +...+a_(k−2) 2^((k−2)−k) +a_(k−1) 2^((k−1)−k) . It is clear that the fractional part of (n/2^k )+(1/2) can only come from the R term. R=2^(−1) +a_(k−1) 2^(−1) +a_(k−2) 2^(−2) +...+a_3 2^(3−k) +a_2 2^(2−k) +a_1 2^(1−k) +a_0 2^(−k) We know that max(a_i )=1 and min(a_i )=0. ∴ 2^(−1) +0+0+0+...+0≤R≤2^(−1) +2^(−1) +2^(−2) +...+2^(3−k) +2^(2−k) +2^(1−k) +2^(−k) (1/2)≤R≤(1/2)+(((1/2)(((1/2))^(k+1) −1))/((1/2)−1)) (1/2)≤R≤(3/2)−(1/2^(k+1) ) for all k∈N. Since k≥1⇒ min((3/2)−(1/2^(k+1) ))=(6/4)−(1/4)=(5/4)>1 ∴(1/2)≤R≤(5/4)<(3/2) ⇒⌊R⌋=0 or ⌊R⌋=1 If (1/2)≤R<1 ⇒⌊R⌋=0⇒⌊(n/2^k )+(1/2)⌋=a_k +a_(k+1) 2+a_(k+2) 2^2 +a_(k+3) 2^3 +...+a_m 2^(m−k) =u(k). ∴ S_k =Σ_(i=1) ^k u(i) S_k =(1/2){2a_1 +2^2 a_2 +2^3 a_3 +2^4 a_4 +...+a_m 2^m } +(1/2^2 ){a_2 2^2 +2^3 a_3 +2^4 a_4 +2^5 a_5 +...+a_m 2^m } +(1/2^3 ){a_3 2^3 +2^4 a_4 +2^5 a_5 +2^6 a_6 +...+a_m 2^m } +...+(1/2^k ){a_k 2^k +a_(k+1) 2^(k+1) +a_(k+2) 2^(k+2) +...+a_m 2^m } S_k =(1/2)(n−a_0 )+(1/2^2 )(n−a_0 −2a_1 )+(1/2^3 )(n−a_0 −2a_1 −2^2 a_2 ) +...+(1/2^k )(n−Σ_(i=0) ^(k−1) a_i 2^i ) S_k =n(((1/2)(1−(1/2^(k+1) )))/(1−(1/2)))−Σ_(j=1) ^k {(1/2^j )Σ_(i=0) ^(j−1) a_i 2^i } S_k =n−[(n/2^(k+1) )+Σ_(j=0) ^k {(1/2^j )Σ_(i=0) ^(j−1) a_i 2^i }] −−−−−−−−−−−−−−−−−−−−−−−−− If k=m⇒(n/2^m )+(1/2)=R where R=2^(−1) +a_0 2^(−m) +a_1 2^(1−m) +a_2 2^(2−m) +a_3 2^(3−m) +...+a_(m−2) 2^(m−2−m) +a_(m−1) 2^(m−1−m) +a_m 2^(m−m) R=2^(−1) +a_m +a_(m−1) (1/2)+a_(m−2) (1/2^2 )+...+a_3 (1/2^(m−3) )+a_2 (1/2^(m−2) )+a_1 (1/2^(m−1) )+a_0 (1/2^m ). 2^(−1) ≤R≤(3/2)+(((1/2)(1−(1/2^(m+1) )))/(1−(1/2))) 2^(−1) ≤R≤(5/2)−(1/2^(m+1) ) ⇒⌊R⌋=0,1,2 −−−−−−−−−−−−−−−−−−−−−−− Continue...](Q7339.png)
$$\left[\frac{{n}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\right]+\left[\frac{{n}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right]+\left[\frac{{n}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{2}}\right]+\left[\frac{{n}}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{2}}\right]+...+\left[\frac{{n}}{\mathrm{2}^{{k}} }+\frac{\mathrm{1}}{\mathrm{2}}\right]={S}_{{k}} \\ $$$${Any}\:{integer}\:{can}\:{be}\:{represented}\:{in} \\ $$$${base}\:\mathrm{2}\:{according}\:{to}\:{the}\:{base}\:{representation}\:{theorem}. \\ $$$$\therefore\:{n}=\underset{{i}=\mathrm{0}} {\overset{{m}} {\sum}}{a}_{{i}} \mathrm{2}^{{i}} \:\:\:{where}\:{each}\:{a}_{{i}} =\mathrm{0}\:\vee\:\mathrm{1}. \\ $$$$\therefore\:\frac{{n}}{\mathrm{2}^{{k}} }+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}+\underset{{i}=\mathrm{0}} {\overset{{m}} {\sum}}{a}_{{i}} \mathrm{2}^{{i}−{k}} . \\ $$$${Now},\:{for}\:{k},{m}\in\mathbb{N},\:{k}<{m}\:{or}\:{k}={m}\:{or}\:{k}>{m}. \\ $$$${If}\:{k}<{m}\:{then}\:{for}\:{some}\:{i}\in\mathbb{Z}^{\geqslant} ,\:{i}−{k}<\mathrm{0} \\ $$$${or}\:{i}<{k}\Rightarrow{i}\leqslant{k}−\mathrm{1}.\:{Hence}\:{we}\:{can}\:{write} \\ $$$$\frac{{n}}{\mathrm{2}^{{k}} }+\frac{\mathrm{1}}{\mathrm{2}}={R}+{a}_{{k}} \mathrm{2}^{{k}−{k}} +{a}_{{k}+\mathrm{1}} \mathrm{2}^{\left({k}+\mathrm{1}\right)−{k}} +{a}_{{k}+\mathrm{2}} \mathrm{2}^{\left({k}+\mathrm{2}\right)−{k}} +...+{a}_{{m}−\mathrm{1}} \mathrm{2}^{\left({m}−\mathrm{1}\right)−{k}} +{a}_{{m}} \mathrm{2}^{{m}−{k}} \\ $$$$\frac{{n}}{\mathrm{2}^{{k}} }+\frac{\mathrm{1}}{\mathrm{2}}={R}+{a}_{{k}} +{a}_{{k}+\mathrm{1}} \mathrm{2}+{a}_{{k}+\mathrm{2}} \mathrm{2}^{\mathrm{2}} +...+{a}_{{m}−\mathrm{1}} \mathrm{2}^{\left({m}−\mathrm{1}\right)−{k}} +{a}_{{m}} \mathrm{2}^{{m}−{k}} \\ $$$${where}\:{R}=\mathrm{2}^{−\mathrm{1}} +{a}_{\mathrm{0}} \mathrm{2}^{\mathrm{0}−{k}} +{a}_{\mathrm{1}} \mathrm{2}^{\mathrm{1}−{k}} +{a}_{\mathrm{2}} \mathrm{2}^{\mathrm{2}−{k}} +{a}_{\mathrm{3}} \mathrm{2}^{\mathrm{3}−{k}} +...+{a}_{{k}−\mathrm{2}} \mathrm{2}^{\left({k}−\mathrm{2}\right)−{k}} +{a}_{{k}−\mathrm{1}} \mathrm{2}^{\left({k}−\mathrm{1}\right)−{k}} . \\ $$$${It}\:{is}\:{clear}\:{that}\:{the}\:{fractional}\:{part}\:{of}\:\frac{{n}}{\mathrm{2}^{{k}} }+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${can}\:{only}\:{come}\:{from}\:{the}\:{R}\:{term}. \\ $$$${R}=\mathrm{2}^{−\mathrm{1}} +{a}_{{k}−\mathrm{1}} \mathrm{2}^{−\mathrm{1}} +{a}_{{k}−\mathrm{2}} \mathrm{2}^{−\mathrm{2}} +...+{a}_{\mathrm{3}} \mathrm{2}^{\mathrm{3}−{k}} +{a}_{\mathrm{2}} \mathrm{2}^{\mathrm{2}−{k}} +{a}_{\mathrm{1}} \mathrm{2}^{\mathrm{1}−{k}} +{a}_{\mathrm{0}} \mathrm{2}^{−{k}} \\ $$$${We}\:{know}\:{that}\:{max}\left({a}_{{i}} \right)=\mathrm{1}\:{and}\:{min}\left({a}_{{i}} \right)=\mathrm{0}. \\ $$$$\therefore\:\mathrm{2}^{−\mathrm{1}} +\mathrm{0}+\mathrm{0}+\mathrm{0}+...+\mathrm{0}\leqslant{R}\leqslant\mathrm{2}^{−\mathrm{1}} +\mathrm{2}^{−\mathrm{1}} +\mathrm{2}^{−\mathrm{2}} +...+\mathrm{2}^{\mathrm{3}−{k}} +\mathrm{2}^{\mathrm{2}−{k}} +\mathrm{2}^{\mathrm{1}−{k}} +\mathrm{2}^{−{k}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\leqslant{R}\leqslant\frac{\mathrm{1}}{\mathrm{2}}+\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{k}+\mathrm{1}} −\mathrm{1}\right)}{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\leqslant{R}\leqslant\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}^{{k}+\mathrm{1}} }\:{for}\:{all}\:{k}\in\mathbb{N}. \\ $$$${Since}\:{k}\geqslant\mathrm{1}\Rightarrow\:{min}\left(\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}^{{k}+\mathrm{1}} }\right)=\frac{\mathrm{6}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{5}}{\mathrm{4}}>\mathrm{1} \\ $$$$\therefore\frac{\mathrm{1}}{\mathrm{2}}\leqslant{R}\leqslant\frac{\mathrm{5}}{\mathrm{4}}<\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\Rightarrow\lfloor{R}\rfloor=\mathrm{0}\:{or}\:\lfloor{R}\rfloor=\mathrm{1} \\ $$$${If}\:\frac{\mathrm{1}}{\mathrm{2}}\leqslant{R}<\mathrm{1}\:\Rightarrow\lfloor{R}\rfloor=\mathrm{0}\Rightarrow\lfloor\frac{{n}}{\mathrm{2}^{{k}} }+\frac{\mathrm{1}}{\mathrm{2}}\rfloor={a}_{{k}} +{a}_{{k}+\mathrm{1}} \mathrm{2}+{a}_{{k}+\mathrm{2}} \mathrm{2}^{\mathrm{2}} +{a}_{{k}+\mathrm{3}} \mathrm{2}^{\mathrm{3}} +...+{a}_{{m}} \mathrm{2}^{{m}−{k}} ={u}\left({k}\right). \\ $$$$\therefore\:{S}_{{k}} =\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}{u}\left({i}\right) \\ $$$${S}_{{k}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{2}{a}_{\mathrm{1}} +\mathrm{2}^{\mathrm{2}} {a}_{\mathrm{2}} +\mathrm{2}^{\mathrm{3}} {a}_{\mathrm{3}} +\mathrm{2}^{\mathrm{4}} {a}_{\mathrm{4}} +...+{a}_{{m}} \mathrm{2}^{{m}} \right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\left\{{a}_{\mathrm{2}} \mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{3}} {a}_{\mathrm{3}} +\mathrm{2}^{\mathrm{4}} {a}_{\mathrm{4}} +\mathrm{2}^{\mathrm{5}} {a}_{\mathrm{5}} +...+{a}_{{m}} \mathrm{2}^{{m}} \right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }\left\{{a}_{\mathrm{3}} \mathrm{2}^{\mathrm{3}} +\mathrm{2}^{\mathrm{4}} {a}_{\mathrm{4}} +\mathrm{2}^{\mathrm{5}} {a}_{\mathrm{5}} +\mathrm{2}^{\mathrm{6}} {a}_{\mathrm{6}} +...+{a}_{{m}} \mathrm{2}^{{m}} \right\} \\ $$$$+...+\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\left\{{a}_{{k}} \mathrm{2}^{{k}} +{a}_{{k}+\mathrm{1}} \mathrm{2}^{{k}+\mathrm{1}} +{a}_{{k}+\mathrm{2}} \mathrm{2}^{{k}+\mathrm{2}} +...+{a}_{{m}} \mathrm{2}^{{m}} \right\} \\ $$$${S}_{{k}} =\frac{\mathrm{1}}{\mathrm{2}}\left({n}−{a}_{\mathrm{0}} \right)+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\left({n}−{a}_{\mathrm{0}} −\mathrm{2}{a}_{\mathrm{1}} \right)+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }\left({n}−{a}_{\mathrm{0}} −\mathrm{2}{a}_{\mathrm{1}} −\mathrm{2}^{\mathrm{2}} {a}_{\mathrm{2}} \right) \\ $$$$+...+\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\left({n}−\underset{{i}=\mathrm{0}} {\overset{{k}−\mathrm{1}} {\sum}}{a}_{{i}} \mathrm{2}^{{i}} \right) \\ $$$${S}_{{k}} ={n}\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{k}+\mathrm{1}} }\right)}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}−\underset{{j}=\mathrm{1}} {\overset{{k}} {\sum}}\left\{\frac{\mathrm{1}}{\mathrm{2}^{{j}} }\underset{{i}=\mathrm{0}} {\overset{{j}−\mathrm{1}} {\sum}}{a}_{{i}} \mathrm{2}^{{i}} \right\} \\ $$$${S}_{{k}} ={n}−\left[\frac{{n}}{\mathrm{2}^{{k}+\mathrm{1}} }+\underset{{j}=\mathrm{0}} {\overset{{k}} {\sum}}\left\{\frac{\mathrm{1}}{\mathrm{2}^{{j}} }\underset{{i}=\mathrm{0}} {\overset{{j}−\mathrm{1}} {\sum}}{a}_{{i}} \mathrm{2}^{{i}} \right\}\right] \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${If}\:{k}={m}\Rightarrow\frac{{n}}{\mathrm{2}^{{m}} }+\frac{\mathrm{1}}{\mathrm{2}}={R} \\ $$$${where}\:{R}=\mathrm{2}^{−\mathrm{1}} +{a}_{\mathrm{0}} \mathrm{2}^{−{m}} +{a}_{\mathrm{1}} \mathrm{2}^{\mathrm{1}−{m}} +{a}_{\mathrm{2}} \mathrm{2}^{\mathrm{2}−{m}} +{a}_{\mathrm{3}} \mathrm{2}^{\mathrm{3}−{m}} +...+{a}_{{m}−\mathrm{2}} \mathrm{2}^{{m}−\mathrm{2}−{m}} +{a}_{{m}−\mathrm{1}} \mathrm{2}^{{m}−\mathrm{1}−{m}} +{a}_{{m}} \mathrm{2}^{{m}−{m}} \\ $$$${R}=\mathrm{2}^{−\mathrm{1}} +{a}_{{m}} +{a}_{{m}−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}+{a}_{{m}−\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+...+{a}_{\mathrm{3}} \frac{\mathrm{1}}{\mathrm{2}^{{m}−\mathrm{3}} }+{a}_{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}^{{m}−\mathrm{2}} }+{a}_{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}^{{m}−\mathrm{1}} }+{a}_{\mathrm{0}} \frac{\mathrm{1}}{\mathrm{2}^{{m}} }. \\ $$$$\mathrm{2}^{−\mathrm{1}} \leqslant{R}\leqslant\frac{\mathrm{3}}{\mathrm{2}}+\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{m}+\mathrm{1}} }\right)}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{2}^{−\mathrm{1}} \leqslant{R}\leqslant\frac{\mathrm{5}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}^{{m}+\mathrm{1}} } \\ $$$$\Rightarrow\lfloor{R}\rfloor=\mathrm{0},\mathrm{1},\mathrm{2} \\ $$$$−−−−−−−−−−−−−−−−−−−−−−− \\ $$$$ \\ $$$${Continue}... \\ $$$$ \\ $$$$ \\ $$
Commented by lakshaysethi last updated on 24/Aug/16

$${yes}\:{sir}\left({to}\:{prakash}\:{jain}\:{sir}\right) \\ $$
