
Question and Answers Forum
Question Number 73179 by mathmax by abdo last updated on 07/Nov/19
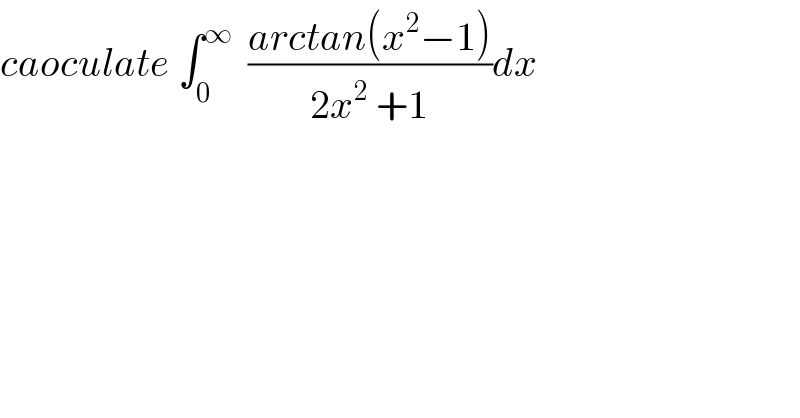
Commented by mathmax by abdo last updated on 07/Nov/19

Answered by mind is power last updated on 07/Nov/19
![∫_0 ^(+∞) ((arctan(x^2 −1))/(2x^2 +1))dx=a ∫(dx/(2x^2 +1))=(1/(√2))arctan(x(√2)) a=[((arctan(x(√2)))/(√2)).arctan(x^2 −1)]_0 ^(+∞) −(1/(√2))∫_0 ^(+∞) ((arctan(x(√2)).2xdx)/((x^2 −1)^2 +1)) a=(π^2 /(4(√2)))−(√2)∫_0 ^(+∞) ((arctan(x(√2))xdx)/((x^2 −1)^2 +1))=(π^2 /(4(√2)))−(1/(√2))∫_(−∞) ^(+∞) ((arctan(x(√2))xdx)/((x^2 −1)^2 +1)) on pose f(t)=∫_(−∞) ^(+∞) ((xarctan(tx))/((x^2 −1)^2 +1))dx t≥0 f′(t)=∫_(−∞) ^(+∞) ((x^2 dx)/((1+x^2 t^2 )(x^2 −1−i)(x^2 −1+i))) pols are x_0 =+(i/t),x^2 =1+i⇒x_2 =(2^(1/4) )e^((iπ)/8) x=−1+i⇒x_1 =(2^(1/4) )e^((i3π)/8) f′(t)=2iπ res(f,x_0 ,x_1 x_2 ) 2iπres(f,(i/t))=2iπ.(((−1)/t^2 )/((2i)t((((1+t^2 )/t^2 ))^2 +1)))=((−πt)/((2t^4 +2t^2 +1))) too be continued](Q73187.png)
| ||
Question and Answers Forum | ||
Question Number 73179 by mathmax by abdo last updated on 07/Nov/19 | ||
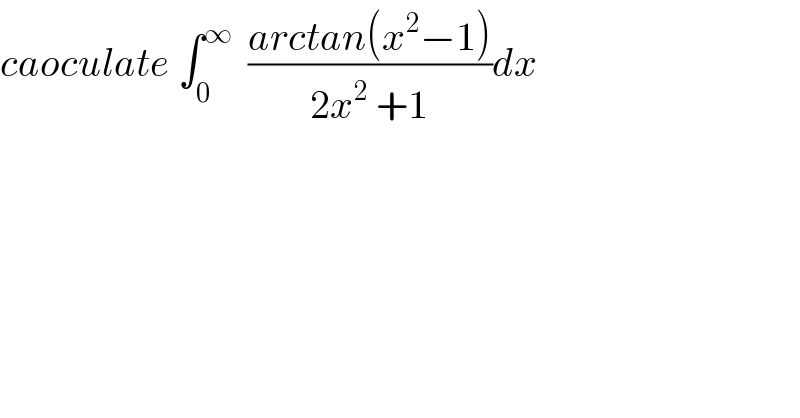 | ||
Commented by mathmax by abdo last updated on 07/Nov/19 | ||
 | ||
Answered by mind is power last updated on 07/Nov/19 | ||
![∫_0 ^(+∞) ((arctan(x^2 −1))/(2x^2 +1))dx=a ∫(dx/(2x^2 +1))=(1/(√2))arctan(x(√2)) a=[((arctan(x(√2)))/(√2)).arctan(x^2 −1)]_0 ^(+∞) −(1/(√2))∫_0 ^(+∞) ((arctan(x(√2)).2xdx)/((x^2 −1)^2 +1)) a=(π^2 /(4(√2)))−(√2)∫_0 ^(+∞) ((arctan(x(√2))xdx)/((x^2 −1)^2 +1))=(π^2 /(4(√2)))−(1/(√2))∫_(−∞) ^(+∞) ((arctan(x(√2))xdx)/((x^2 −1)^2 +1)) on pose f(t)=∫_(−∞) ^(+∞) ((xarctan(tx))/((x^2 −1)^2 +1))dx t≥0 f′(t)=∫_(−∞) ^(+∞) ((x^2 dx)/((1+x^2 t^2 )(x^2 −1−i)(x^2 −1+i))) pols are x_0 =+(i/t),x^2 =1+i⇒x_2 =(2^(1/4) )e^((iπ)/8) x=−1+i⇒x_1 =(2^(1/4) )e^((i3π)/8) f′(t)=2iπ res(f,x_0 ,x_1 x_2 ) 2iπres(f,(i/t))=2iπ.(((−1)/t^2 )/((2i)t((((1+t^2 )/t^2 ))^2 +1)))=((−πt)/((2t^4 +2t^2 +1))) too be continued](Q73187.png) | ||
| ||