Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 73261 by mathmax by abdo last updated on 09/Nov/19

$$calculate\sum _{n=1}^{\mathrm{\infty }}(n^4+2n^2-3)\frac{x^n}{n!}incaseofconvergence.$$

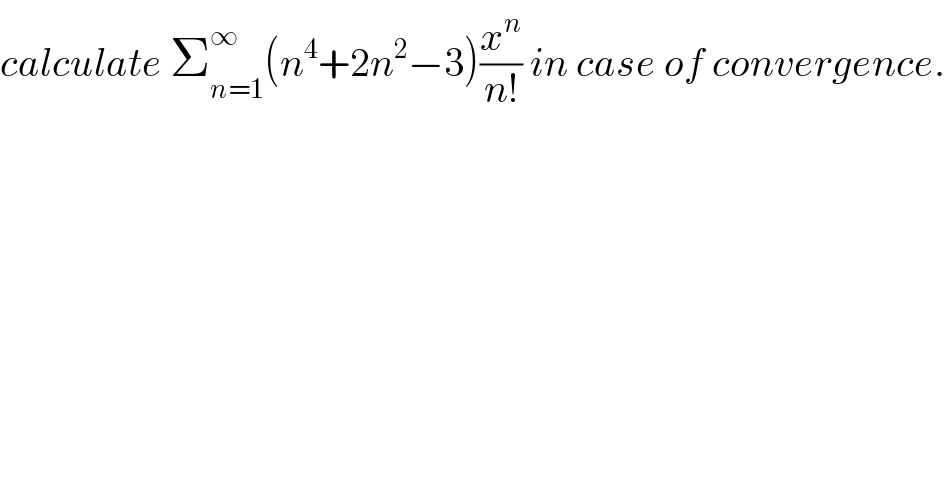
Commented by mathmax by abdo last updated on 09/Nov/19

$$wehave\sum _{n=1}^{\mathrm{\infty }}(n^4+2n^2-3)\frac{x^n}{n!}=\sum _{n=1}^{\mathrm{\infty }}\frac{n^3}{(n-1)!}{x}^n+2\sum _{n=1}^{\mathrm{\infty }}\frac{{nx}^n}{(n-1)!}$$$$-3\sum _{n=1}^{\mathrm{\infty }}\frac{x^n}{n!}wehavefirst\sum _{n=1}^{\mathrm{\infty }}\frac{x^n}{n!}=e^x-1$$$$\sum _{n=1}^{\mathrm{\infty }}\frac{{nx}^n}{(n-1)!}=\sum _{n=0}^{\mathrm{\infty }}\frac{(n+1)x^{n+1}}{n!}=\sum _{n=1}^{\mathrm{\infty }}\frac{x^{n+1}}{(n-1)!}+\sum _{n=0}^{\mathrm{\infty }}\frac{x^{n+1}}{n!}$$$$=x\sum _{n=0}^{\mathrm{\infty }}\frac{x^{n+1}}{n!}+x{e}^x=x^2{e}^x+{xe}^x$$$$\sum _{n=1}^{\mathrm{\infty }}\frac{n^3}{(n-1)!}{x}^n=\sum _{n=0}^{\mathrm{\infty }}\frac{{(n+1)}^3}{n!}{x}^{n+1}$$$$=\sum _{n=0}^{\mathrm{\infty }}\frac{n^3+3n^2+n+1}{n!}{x}^{n+1}=\sum _{n=1}^{\mathrm{\infty }}\frac{n^2}{(n-1)!}{x}^{n+1}+3\sum _{n=1}^{\mathrm{\infty }}\frac{n}{(n-1)!}{x}^{n+1}$$$$+\sum _{n=0}^{\mathrm{\infty }}\frac{x^{n+1}}{(n-1)!}+\sum _{n=0}^{\mathrm{\infty }}\frac{x^{n+1}}{n!}$$$$\sum _{n=1}^{\mathrm{\infty }}\frac{n^2}{(n-1)!}{x}^{n+1}=\sum _{n=0}^{\mathrm{\infty }}\frac{{(n+1)}^2{x}^{n+2}}{n!}$$$$=\sum _{n=0}^{\mathrm{\infty }}\frac{n^2+2n+1}{n!}{x}^{n+2}=\sum _{n=1}^{\mathrm{\infty }}\frac{n}{(n-1)!}{x}^{n+2}+2\sum _{n=1}^{\mathrm{\infty }}\frac{1}{(n-1)!}{x}^{n+2}$$$$+x^2{e}^x$$$$=\sum _{n=0}^{\mathrm{\infty }}\frac{n+1}{n!}{x}^{n+2}+2\sum _{n=0}^{\mathrm{\infty }}\frac{x^{n+3}}{n!}+x^2{e}^x$$$$=\sum _{n=1}^{\mathrm{\infty }}\frac{x^{n+2}}{(n-1)!}+x^2{e}^x+2x^3{e}^x+x^2{e}^x$$$$=\sum _{n=0}^{\mathrm{\infty }}\frac{x^{n+3}}{n!}+2x^2{e}^x+2x^3{e}^x$$$$=x^3{e}^x+2x^3{e}^x+2x^2{e}^x=(3x^3+2x^2)e^x...becontinued...$$

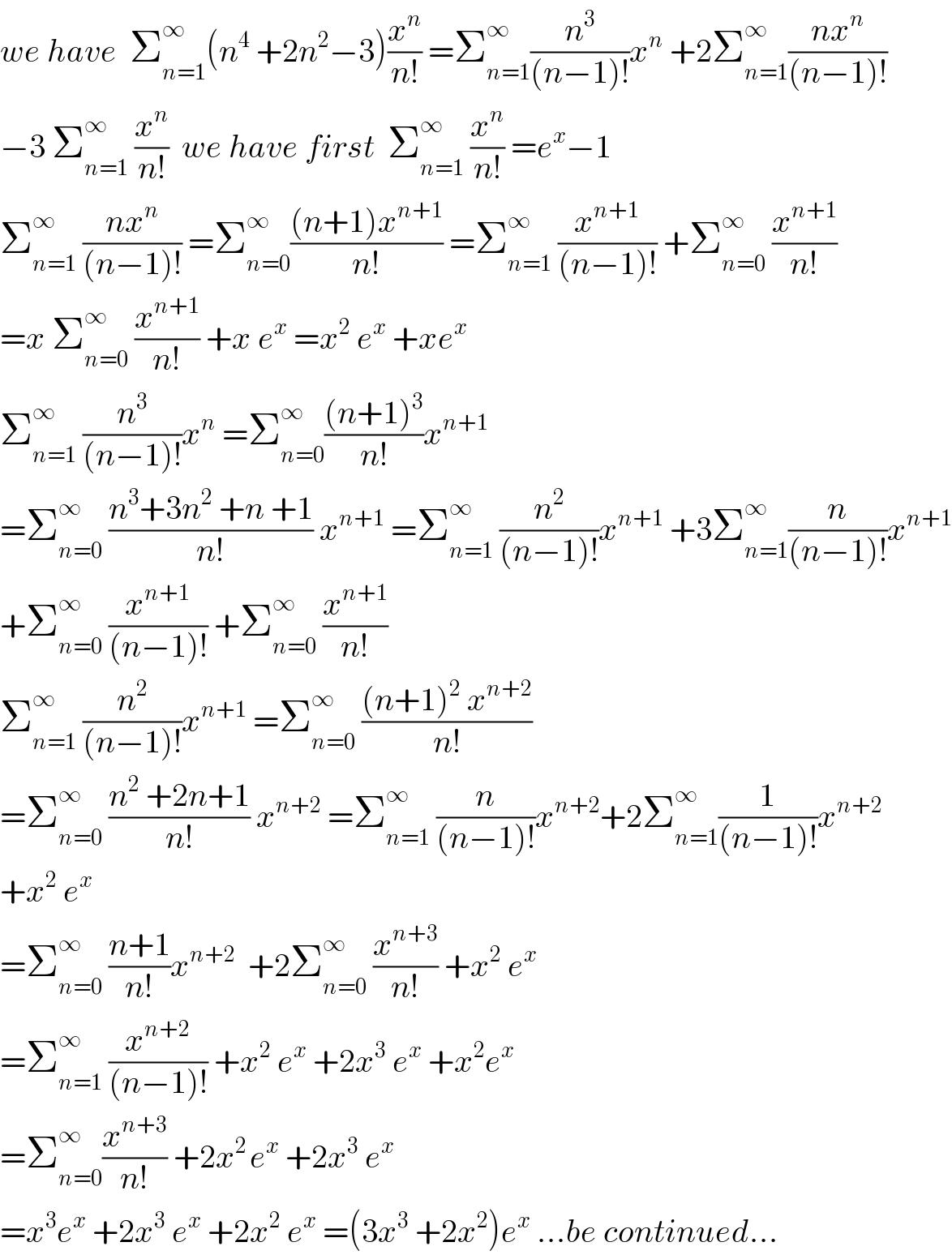
Answered by mind is power last updated on 09/Nov/19

$$\mathrm{use}1,\mathrm{x},\mathrm{x}(\mathrm{x}-1),\mathrm{x}(\mathrm{x}-1)(\mathrm{x}-2),\mathrm{x}(\mathrm{x}-1)(\mathrm{x}-2)(\mathrm{x}-3)$$$$\mathrm{as}\mathrm{Base}\mathrm{of}{\mathrm{IR}}^4\left[\mathrm{X}\right]$$$${\mathrm{n}}^4+{2\mathrm{n}}^2-3=\mathrm{an}(\mathrm{n}-1)(\mathrm{n}-2)(\mathrm{n}-3)+\mathrm{bn}(\mathrm{n}-1)(\mathrm{n}-2)+\mathrm{cn}(\mathrm{n}-1)+\mathrm{dn}+\mathrm{t}$$$$\sum _{\mathrm{n}⩾1}({\mathrm{n}}^4+{2\mathrm{n}}^2-3)\frac{{\mathrm{x}}^{\mathrm{n}}}{\mathrm{n}!}=\sum _{\mathrm{n}⩾4}\left(\mathrm{a}\frac{{\mathrm{x}}^{\mathrm{n}}}{(\mathrm{n}-4)!}\right)+\mathrm{b}\sum _{\mathrm{n}⩾4}\frac{{\mathrm{x}}^{\mathrm{n}}}{(\mathrm{n}-3))!}+\mathrm{c}\sum _{\mathrm{n}⩾4}\frac{{\mathrm{x}}^{\mathrm{n}}}{(\mathrm{n}-2)!}+\mathrm{d}\sum _{\mathrm{n}⩾4}\frac{{\mathrm{x}}^{\mathrm{n}}}{(\mathrm{n}-1)!}+\mathrm{t}\sum _{\mathrm{n}⩾4}\frac{{\mathrm{x}}^{\mathrm{n}}}{\mathrm{n}!}$$$$+\{\underset{\mathrm{n}=1}{\sum ^3}({\mathrm{n}}^4+{2\mathrm{n}}^2-3)\frac{{\mathrm{x}}^{\mathrm{n}}}{\mathrm{n}!}=\mathrm{h}\left(\mathrm{x}\right)\}$$$$={\mathrm{ax}}^4{\mathrm{e}}^{\mathrm{x}}+{\mathrm{bx}}^3({\mathrm{e}}^{\mathrm{x}}-1)+{\mathrm{cx}}^2({\mathrm{e}}^{\mathrm{x}}-1-\mathrm{x})+\mathrm{dx}({\mathrm{e}}^{\mathrm{x}}-1-\mathrm{x}-\frac{{\mathrm{x}}^2}{2})+\mathrm{t}({\mathrm{e}}^{\mathrm{x}}-1-\mathrm{x}-\frac{{\mathrm{x}}^2}{2}-\frac{{\mathrm{x}}^3}{6})+\mathrm{h}\left(\mathrm{x}\right)$$$$$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com