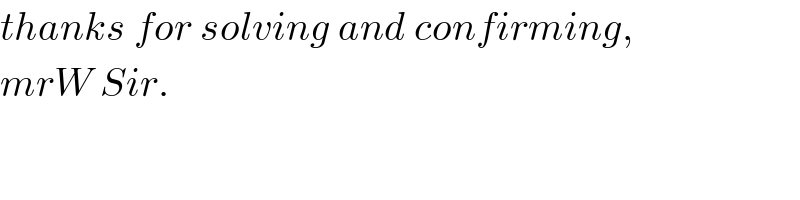Question Number 73297 by mr W last updated on 10/Nov/19
Commented by mr W last updated on 10/Nov/19
$${a}\:{block}\:{of}\:{mass}\:{m}\:{is}\:{released}\:{at}\:{the} \\ $$$${top}\:{of}\:{a}\:{hemisphere}. \\ $$$${find}\:{the}\:{time}\:{for}\:{the}\:{block}\:{to}\:{hit}\:{the} \\ $$$${ground}\:{and}\:{the}\:{position}\:{of}\:{the}\:{hit}. \\ $$$${the}\:{hemisphere}\:{is}\:{fixed}\:{on}\:{the}\:{ground} \\ $$$${and}\:{there}\:{is}\:{no}\:{friction}. \\ $$
Answered by ajfour last updated on 10/Nov/19
![let angle descended until in contact be θ. mgcos θ=((mv^2 )/R) ((mv^2 )/2)=mgR(1−cos θ) ⇒ mgRcos θ=2mgR(1−cos θ) ⇒ θ=cos^(−1) (2/3) v=(√((2gR)/3)) (vcos θ)t=d−Rsin θ ⇒ d=(((√5)R)/3)+((2vt)/3) .....(i) Rcos θ=(vsin θ)t+((gt^2 )/2) ⇒ ((2R)/3)=(((√5)v)/3)t+((gt^2 )/2) ⇒ 3gt^2 +2(√5)vt−4R=0 t=((−2(√5)v+(√(20v^2 +48Rg)))/(6g)) =((−2(√5)(√((2gR)/3))+(√((((40)/3)+48)Rg)))/(6g)) t =(√(R/g))×((((√(46))−(√(10))))/(3(√3))) ....(ii) Now from (i) d=(((√5)R)/3)+((2vt)/3) time for circular arc path_(−) mgsin φ=((mdv)/dt) v=(√(2gR(1−cos φ)))=2(√(gR))sin (φ/2) dv=(√(gR))cos (φ/2)dφ ⇒ ∫_0 ^( T) dt=(√(R/g))∫_0 ^( θ) ((cos (φ/2))/(2sin (φ/2)cos (φ/2)))dφ T = (√(R/g))ln ∣(1/(sin (φ/2)))−(1/(tan (φ/2)))∣_0 ^θ T =(√(R/g)){ln ((1/(sin (θ/2)))−(1/(tan (θ/2)))) −lim_(φ→0) ln (((2sin^2 (φ/4))/(2sin (φ/4)cos (φ/4))))} second term→−∞ T not defined. tan θ=((2tan (θ/2))/(1−tan^2 (θ/2))) let tan (θ/2)=z ⇒ ((√5)/2)=((2z)/(1−z^2 )) ⇒ z^2 +(4/(√5))z−1=0 ⇒ z=((−(4/(√5))+(√(((16)/5)+4)))/2) tan (θ/2)=(1/(√5)) d=(((√5)R)/3)+(2/3)(√((2gR)/3))[(√(R/g))×((((√(46))−(√(10))))/(3(√3)))] ⇒ d=(R/3){(√5)+((2(√2))/9)((√(46))−(√(10)))} =(((4(√(23))+5(√5))/(27)))R . t_(total) =T+(√(R/g)){((((√(46))−(√(10))))/(3(√3)))} T is not defined.](Q73303.png)
$${let}\:{angle}\:{descended}\:{until}\:{in}\: \\ $$$${contact}\:{be}\:\theta. \\ $$$${mg}\mathrm{cos}\:\theta=\frac{{mv}^{\mathrm{2}} }{{R}} \\ $$$$\frac{{mv}^{\mathrm{2}} }{\mathrm{2}}={mgR}\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$$\Rightarrow\:\:{mgR}\mathrm{cos}\:\theta=\mathrm{2}{mgR}\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$$\Rightarrow\:\:\theta=\mathrm{cos}^{−\mathrm{1}} \left(\mathrm{2}/\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:{v}=\sqrt{\frac{\mathrm{2}{gR}}{\mathrm{3}}} \\ $$$$\:\:\left({v}\mathrm{cos}\:\theta\right){t}={d}−{R}\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\:{d}=\frac{\sqrt{\mathrm{5}}{R}}{\mathrm{3}}+\frac{\mathrm{2}{vt}}{\mathrm{3}}\:\:\:\:\:\:\:\:\:\:.....\left({i}\right) \\ $$$$\:\:{R}\mathrm{cos}\:\theta=\left({v}\mathrm{sin}\:\theta\right){t}+\frac{{gt}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow\:\:\frac{\mathrm{2}{R}}{\mathrm{3}}=\frac{\sqrt{\mathrm{5}}{v}}{\mathrm{3}}{t}+\frac{{gt}^{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{3}{gt}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{5}}{vt}−\mathrm{4}{R}=\mathrm{0} \\ $$$$\:\:{t}=\frac{−\mathrm{2}\sqrt{\mathrm{5}}{v}+\sqrt{\mathrm{20}{v}^{\mathrm{2}} +\mathrm{48}{Rg}}}{\mathrm{6}{g}} \\ $$$$\:\:\:\:=\frac{−\mathrm{2}\sqrt{\mathrm{5}}\sqrt{\frac{\mathrm{2}{gR}}{\mathrm{3}}}+\sqrt{\left(\frac{\mathrm{40}}{\mathrm{3}}+\mathrm{48}\right){Rg}}}{\mathrm{6}{g}} \\ $$$$\:\:\:{t}\:=\sqrt{\frac{{R}}{{g}}}×\frac{\left(\sqrt{\mathrm{46}}−\sqrt{\mathrm{10}}\right)}{\mathrm{3}\sqrt{\mathrm{3}}}\:\:\:\:\:\:....\left({ii}\right) \\ $$$${Now}\:{from}\:\left({i}\right) \\ $$$${d}=\frac{\sqrt{\mathrm{5}}{R}}{\mathrm{3}}+\frac{\mathrm{2}{vt}}{\mathrm{3}} \\ $$$$\underset{−} {{time}\:{for}\:{circular}\:{arc}\:{path}} \\ $$$$\:\:\:{mg}\mathrm{sin}\:\phi=\frac{{mdv}}{{dt}} \\ $$$$\:\:\:{v}=\sqrt{\mathrm{2}{gR}\left(\mathrm{1}−\mathrm{cos}\:\phi\right)}=\mathrm{2}\sqrt{{gR}}\mathrm{sin}\:\frac{\phi}{\mathrm{2}} \\ $$$$\:\:{dv}=\sqrt{{gR}}\mathrm{cos}\:\frac{\phi}{\mathrm{2}}{d}\phi \\ $$$$\Rightarrow\:\:\int_{\mathrm{0}} ^{\:{T}} {dt}=\sqrt{\frac{{R}}{{g}}}\int_{\mathrm{0}} ^{\:\theta} \frac{\mathrm{cos}\:\left(\phi/\mathrm{2}\right)}{\mathrm{2sin}\:\frac{\phi}{\mathrm{2}}\mathrm{cos}\:\frac{\phi}{\mathrm{2}}}{d}\phi \\ $$$$\:\:\:{T}\:=\:\sqrt{\frac{{R}}{{g}}}\mathrm{ln}\:\mid\frac{\mathrm{1}}{\mathrm{sin}\:\frac{\phi}{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\phi}{\mathrm{2}}}\mid_{\mathrm{0}} ^{\theta} \\ $$$$\:\:\:\:{T}\:=\sqrt{\frac{{R}}{{g}}}\left\{\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}−\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}\right)\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:−\underset{\phi\rightarrow\mathrm{0}} {\mathrm{lim}ln}\:\left(\frac{\mathrm{2sin}\:^{\mathrm{2}} \frac{\phi}{\mathrm{4}}}{\mathrm{2sin}\:\frac{\phi}{\mathrm{4}}\mathrm{cos}\:\frac{\phi}{\mathrm{4}}}\right)\right\} \\ $$$${second}\:{term}\rightarrow−\infty \\ $$$${T}\:{not}\:{defined}. \\ $$$$\:\:\mathrm{tan}\:\theta=\frac{\mathrm{2tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \frac{\theta}{\mathrm{2}}}\:\:\:\:{let}\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}={z} \\ $$$$\Rightarrow\:\:\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}=\frac{\mathrm{2}{z}}{\mathrm{1}−{z}^{\mathrm{2}} }\:\:\:\Rightarrow\:\:{z}^{\mathrm{2}} +\frac{\mathrm{4}}{\sqrt{\mathrm{5}}}{z}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:{z}=\frac{−\frac{\mathrm{4}}{\sqrt{\mathrm{5}}}+\sqrt{\frac{\mathrm{16}}{\mathrm{5}}+\mathrm{4}}}{\mathrm{2}} \\ $$$$\:\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\frac{\mathrm{1}}{\sqrt{\mathrm{5}}} \\ $$$${d}=\frac{\sqrt{\mathrm{5}}{R}}{\mathrm{3}}+\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\frac{\mathrm{2}{gR}}{\mathrm{3}}}\left[\sqrt{\frac{{R}}{{g}}}×\frac{\left(\sqrt{\mathrm{46}}−\sqrt{\mathrm{10}}\right)}{\mathrm{3}\sqrt{\mathrm{3}}}\right] \\ $$$$\Rightarrow \\ $$$$\:{d}=\frac{{R}}{\mathrm{3}}\left\{\sqrt{\mathrm{5}}+\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{9}}\left(\sqrt{\mathrm{46}}−\sqrt{\mathrm{10}}\right)\right\} \\ $$$$\:\:=\left(\frac{\mathrm{4}\sqrt{\mathrm{23}}+\mathrm{5}\sqrt{\mathrm{5}}}{\mathrm{27}}\right){R}\:. \\ $$$${t}_{{total}} ={T}+\sqrt{\frac{{R}}{{g}}}\left\{\frac{\left(\sqrt{\mathrm{46}}−\sqrt{\mathrm{10}}\right)}{\mathrm{3}\sqrt{\mathrm{3}}}\right\} \\ $$$${T}\:{is}\:{not}\:{defined}. \\ $$
Commented by mr W last updated on 10/Nov/19
$${thanks}\:{sir}! \\ $$$${time}\:{along}\:{hemisphere}\:{is}\:{not}\:{to} \\ $$$${determine},\:{it}'{s}\:+\infty. \\ $$
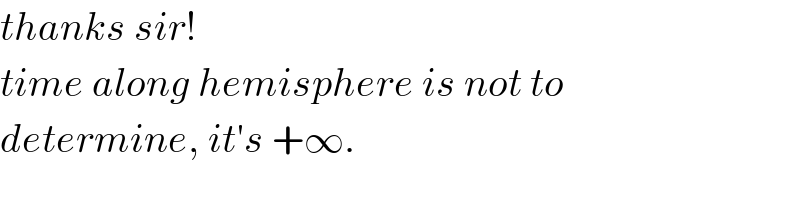
Answered by mr W last updated on 10/Nov/19
Commented by mr W last updated on 10/Nov/19
![at θ: (1/2)mv^2 =mgR(1−cos θ) v=(√(2gR(1−cos θ)))=2(√(gR)) sin (θ/2) v=R(dθ/dt) (dθ/dt)=2(√(g/R)) sin (θ/2) ∫_0 ^θ ((d((θ/2)))/(sin (θ/2)))=(√(g/R))∫_0 ^t_1 dt −∫_0 ^θ ((d(cos (θ/2)))/(1−cos^2 (θ/2)))=t_1 (√(g/R)) (1/2)[ln ((1−cos (θ/2))/(1+cos (θ/2)))]_0 ^θ =t_1 (√(g/R)) let F(θ)=ln ((1−cos (θ/2))/(1+cos (θ/2))) ⇒t_1 =(1/2)(√(R/g)) [F(θ)−lim_(θ→0) F(θ)] since lim_(θ→0) F(θ)=−∞, t_1 can not be determined, t_1 →+∞. at θ=ϕ: N=0 mg cos ϕ=m(v^2 /R)=2mg(1−cos ϕ) cos ϕ=2(1−cos ϕ) ⇒cos ϕ=(2/3)=2 cos^2 (ϕ/2)−1 ⇒cos (ϕ/2)=(√(5/6)), sin (ϕ/2)=(1/(√6)) ⇒sin ϕ=((√5)/3) v=(2/(√6))(√(gR)) R cos ϕ=v sin ϕ t_2 +(1/2)gt_2 ^2 0=−(4/3)+((2(√(30)))/9) ((√(g/R))t_2 )+((√(g/R))t_2 )^2 ⇒(√(g/R))t_2 =(((√(138))−(√(30)))/9) ⇒t_2 =(((√(138))−(√(30)))/9)(√(R/g)) d=R sin ϕ+v cos ϕ t_2 d=R ((√5)/3)+(2/(√6))×(2/3)×((((√(138))−(√(30)))R)/9) d=(((4(√(23))+5(√5))R)/(27))≈1.124R](Q73342.png)
$${at}\:\theta: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{mv}^{\mathrm{2}} ={mgR}\left(\mathrm{1}−\mathrm{cos}\:\theta\right) \\ $$$${v}=\sqrt{\mathrm{2}{gR}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}=\mathrm{2}\sqrt{{gR}}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}} \\ $$$${v}={R}\frac{{d}\theta}{{dt}} \\ $$$$\frac{{d}\theta}{{dt}}=\mathrm{2}\sqrt{\frac{{g}}{{R}}}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\theta} \frac{{d}\left(\frac{\theta}{\mathrm{2}}\right)}{\mathrm{sin}\:\frac{\theta}{\mathrm{2}}}=\sqrt{\frac{{g}}{{R}}}\int_{\mathrm{0}} ^{{t}_{\mathrm{1}} } {dt} \\ $$$$−\int_{\mathrm{0}} ^{\theta} \frac{{d}\left(\mathrm{cos}\:\frac{\theta}{\mathrm{2}}\right)}{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}={t}_{\mathrm{1}} \sqrt{\frac{{g}}{{R}}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ln}\:\frac{\mathrm{1}−\mathrm{cos}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}+\mathrm{cos}\:\frac{\theta}{\mathrm{2}}}\right]_{\mathrm{0}} ^{\theta} ={t}_{\mathrm{1}} \sqrt{\frac{{g}}{{R}}} \\ $$$${let}\:{F}\left(\theta\right)=\mathrm{ln}\:\frac{\mathrm{1}−\mathrm{cos}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}+\mathrm{cos}\:\frac{\theta}{\mathrm{2}}} \\ $$$$\Rightarrow{t}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{{R}}{{g}}}\:\left[{F}\left(\theta\right)−\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}{F}\left(\theta\right)\right] \\ $$$${since}\:\underset{\theta\rightarrow\mathrm{0}} {\mathrm{lim}}{F}\left(\theta\right)=−\infty,\:{t}_{\mathrm{1}} \:{can}\:{not}\:{be} \\ $$$${determined},\:{t}_{\mathrm{1}} \rightarrow+\infty. \\ $$$$ \\ $$$${at}\:\theta=\varphi: \\ $$$${N}=\mathrm{0} \\ $$$${mg}\:\mathrm{cos}\:\varphi={m}\frac{{v}^{\mathrm{2}} }{{R}}=\mathrm{2}{mg}\left(\mathrm{1}−\mathrm{cos}\:\varphi\right) \\ $$$$\mathrm{cos}\:\varphi=\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\varphi\right) \\ $$$$\Rightarrow\mathrm{cos}\:\varphi=\frac{\mathrm{2}}{\mathrm{3}}=\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\varphi}{\mathrm{2}}−\mathrm{1} \\ $$$$\Rightarrow\mathrm{cos}\:\frac{\varphi}{\mathrm{2}}=\sqrt{\frac{\mathrm{5}}{\mathrm{6}}},\:\mathrm{sin}\:\frac{\varphi}{\mathrm{2}}=\frac{\mathrm{1}}{\sqrt{\mathrm{6}}} \\ $$$$\Rightarrow\mathrm{sin}\:\varphi=\frac{\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$$${v}=\frac{\mathrm{2}}{\sqrt{\mathrm{6}}}\sqrt{{gR}} \\ $$$${R}\:\mathrm{cos}\:\varphi={v}\:\mathrm{sin}\:\varphi\:{t}_{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{gt}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$$\mathrm{0}=−\frac{\mathrm{4}}{\mathrm{3}}+\frac{\mathrm{2}\sqrt{\mathrm{30}}}{\mathrm{9}}\:\left(\sqrt{\frac{{g}}{{R}}}{t}_{\mathrm{2}} \right)+\left(\sqrt{\frac{{g}}{{R}}}{t}_{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\Rightarrow\sqrt{\frac{{g}}{{R}}}{t}_{\mathrm{2}} =\frac{\sqrt{\mathrm{138}}−\sqrt{\mathrm{30}}}{\mathrm{9}} \\ $$$$\Rightarrow{t}_{\mathrm{2}} =\frac{\sqrt{\mathrm{138}}−\sqrt{\mathrm{30}}}{\mathrm{9}}\sqrt{\frac{{R}}{{g}}} \\ $$$$ \\ $$$${d}={R}\:\mathrm{sin}\:\varphi+{v}\:\mathrm{cos}\:\varphi\:{t}_{\mathrm{2}} \\ $$$${d}={R}\:\frac{\sqrt{\mathrm{5}}}{\mathrm{3}}+\frac{\mathrm{2}}{\sqrt{\mathrm{6}}}×\frac{\mathrm{2}}{\mathrm{3}}×\frac{\left(\sqrt{\mathrm{138}}−\sqrt{\mathrm{30}}\right){R}}{\mathrm{9}} \\ $$$${d}=\frac{\left(\mathrm{4}\sqrt{\mathrm{23}}+\mathrm{5}\sqrt{\mathrm{5}}\right){R}}{\mathrm{27}}\approx\mathrm{1}.\mathrm{124}{R} \\ $$
Commented by ajfour last updated on 11/Nov/19
$${thanks}\:{for}\:{solving}\:{and}\:{confirming}, \\ $$$${mrW}\:{Sir}. \\ $$