
Question and Answers Forum
Question Number 7331 by rohit meena last updated on 23/Aug/16
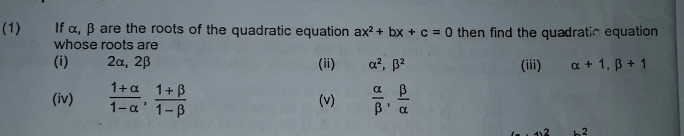
Commented by sandy_suhendra last updated on 24/Aug/16
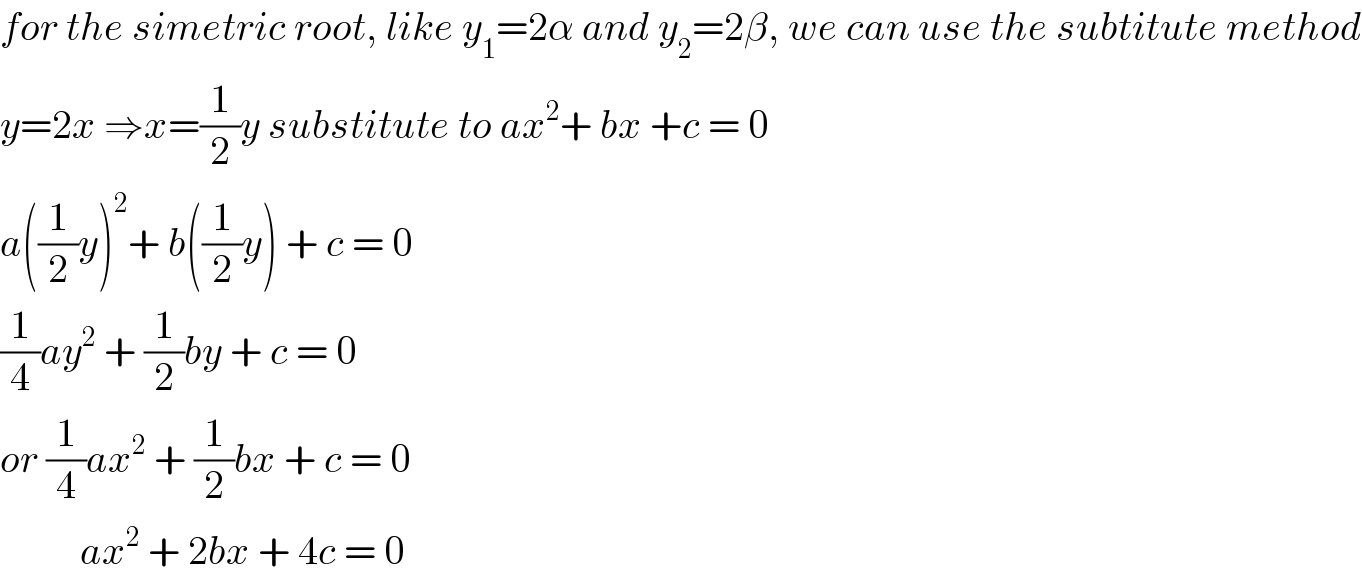
Commented by Rasheed Soomro last updated on 24/Aug/16

Commented by sandy_suhendra last updated on 25/Aug/16
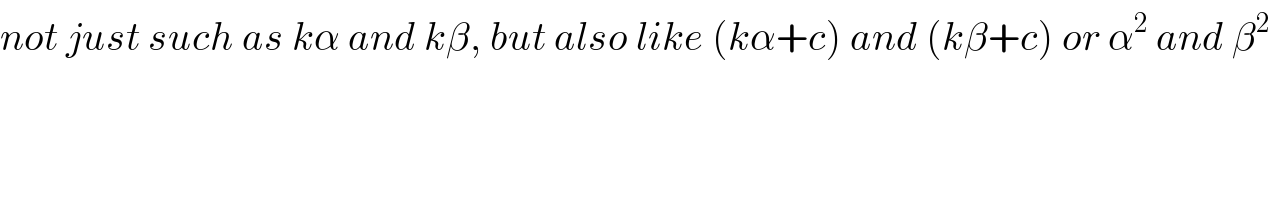
Commented by Rasheed Soomro last updated on 25/Aug/16

Answered by Rasheed Soomro last updated on 24/Aug/16

