find f(x)=∫_0 ^1 e^(−t) ln(1−xt^2 )dt with ∣x∣<1 2)calculate ∫


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 73397 by mathmax by abdo last updated on 11/Nov/19

$f i n d f (x) = \int_{0}^{1} e^{- t} l n (1 - {x t}^{2}) d t w i t h ∣ x ∣< 1$ $2) c a l c u l a t e \int_{0}^{1} e^{- t} l n (1 - \frac{t^{2}}{2}) d t$
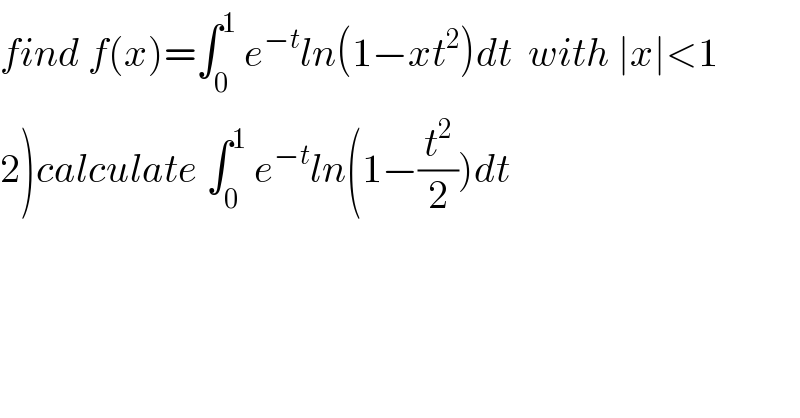
Commented byabdomathmax last updated on 12/Nov/19
$1) we have ln^′ (1−u)=((−1)/(1−u)) =−Σ_(n=0) ^∞ u^n if ∣u∣<1 ⇒ ln(1−u) =−Σ_(n=0) ^∞ (u^(n+1) /(n+1)) +c (c=0) ⇒ ln(1−u) =−Σ_(n=1) ^∞ (u^n /n) we have ∣xt^2 ∣<1 ⇒ ln(1−xt^2 ) =−Σ_(n=1) ^∞ ((x^n t^(2n) )/n) ⇒ f(x)=−∫_0 ^1 e^(−t) (Σ_(n=1) ^∞ ((x^n t^(2n) )/n))dt =−Σ_(n=1) ^∞ (x^n /n) ∫_0 ^1 t^(2n) e^(−t) dt =−Σ_(n=1) ^∞ A_n (x^n /n) with A_n =∫_0 ^1 t^(2n) e^(−t) dt let determinate I_n =∫_0 ^1 t^n e^(−t) dt by parts u=t^n and v^′ =e^(−t) ⇒ I_n =[−e^(−t) t^n ]_0 ^1 +∫_0 ^1 nt^(n−1) e^(−t) dt =−e^(−1) +n I_(n−1) =nI_(n−1) −(1/e) (n>0) let W_n =(I_n /(n!)) ⇒W_(n+1) =(I_(n+1) /((n+1)!)) =(((n+1)I_n −(1/e))/((n+1)!)) =(I_n /(n!)) −(1/(e(n+1)!)) =W_n −(1/(e(n+1)!)) ⇒ W_(n+1) −W_n =−(1/(e(n+1)!)) ⇒ Σ_(k=0) ^(n−1) (W_(k+1) −W_k ) =−(1/e)Σ_(k=0) ^(n−1) (1/((k+1)!)) ⇒W_n =W_0 −(1/e) Σ_(k=1) ^n (1/(k!)) we have W_0 =I_0 =∫_0 ^1 e^(−t) dt =[−e^(−t) ]_0 ^1 =1−e^(−1) ⇒W_n =1−e^(−1) −(1/e)Σ_(k=1) ^n (1/(k!)) ⇒ I_n =n!W_n =n!{1−e^(−1) −e^(−1) Σ_(k=1) ^n (1/(k!))} ⇒ A_n =(2n)!{1−e^(−1) −e^(−1) Σ_(k=1) ^(2n) (1/(k!))} ⇒ f(x)=−Σ_(n=1) ^∞ (2n)!{1−e^(−1) −e^(−1) Σ_(k=1) ^(2n) (1/(k!))}(x^n /n) =(e^(−1) −1)Σ_(n=1) ^∞ (((2n)!)/n) x^n +e^(−1) Σ_(n=1) ^∞ (((2n)!)/n)(Σ_(k=1) ^(2n) (1/(k!)))x^n .....be continued....$
$1) w e h a v e {l n}^{^{'}} (1 - u) = \frac{- 1}{1 - u} = - \sum_{n = 0}^{\infty} u^{n} i f ∣ u ∣< 1 \Rightarrow$ $l n (1 - u) = - \sum_{n = 0}^{\infty} \frac{u^{n + 1}}{n + 1} + c (c = 0) \Rightarrow$ $l n (1 - u) = - \sum_{n = 1}^{\infty} \frac{u^{n}}{n} w e h a v e ∣ {x t}^{2} ∣< 1 \Rightarrow$ $l n (1 - {x t}^{2}) = - \sum_{n = 1}^{\infty} \frac{x^{n} t^{2 n}}{n} \Rightarrow$ $f (x) = - \int_{0}^{1} e^{- t} (\sum_{n = 1}^{\infty} \frac{x^{n} t^{2 n}}{n}) d t$ $= - \sum_{n = 1}^{\infty} \frac{x^{n}}{n} \int_{0}^{1} t^{2 n} e^{- t} d t = - \sum_{n = 1}^{\infty} A_{n} \frac{x^{n}}{n} w i t h$ $A_{n} = \int_{0}^{1} t^{2 n} e^{- t} d t l e t d e t e r m i n a t e I_{n} = \int_{0}^{1} t^{n} e^{- t} d t$ $b y p a r t s u = t^{n} a n d v^{^{'}} = e^{- t} \Rightarrow$ $I_{n} = {[- e^{- t} t^{n}]}_{0}^{1} + \int_{0}^{1} {n t}^{n - 1} e^{- t} d t$ $= - e^{- 1} + n I_{n - 1} = {n I}_{n - 1} - \frac{1}{e} (n > 0)$ $l e t W_{n} = \frac{I_{n}}{n!} \Rightarrow W_{n + 1} = \frac{I_{n + 1}}{(n + 1)!} = \frac{(n + 1) I_{n} - \frac{1}{e}}{(n + 1)!}$ $= \frac{I_{n}}{n!} - \frac{1}{e (n + 1)!} = W_{n} - \frac{1}{e (n + 1)!} \Rightarrow$ $W_{n + 1} - W_{n} = - \frac{1}{e (n + 1)!} \Rightarrow$ $\sum_{k = 0}^{n - 1} (W_{k + 1} - W_{k}) = - \frac{1}{e} \sum_{k = 0}^{n - 1} \frac{1}{(k + 1)!}$ $\Rightarrow W_{n} = W_{0} - \frac{1}{e} \sum_{k = 1}^{n} \frac{1}{k!} w e h a v e W_{0} = I_{0} = \int_{0}^{1} e^{- t} d t$ $= {[- e^{- t}]}_{0}^{1} = 1 - e^{- 1} \Rightarrow W_{n} = 1 - e^{- 1} - \frac{1}{e} \sum_{k = 1}^{n} \frac{1}{k!} \Rightarrow$ $I_{n} = n! W_{n} = n! {1 - e^{- 1} - e^{- 1} \sum_{k = 1}^{n} \frac{1}{k!}} \Rightarrow$ $A_{n} = (2 n)! {1 - e^{- 1} - e^{- 1} \sum_{k = 1}^{2 n} \frac{1}{k!}} \Rightarrow$ $f (x) = - \sum_{n = 1}^{\infty} (2 n)! {1 - e^{- 1} - e^{- 1} \sum_{k = 1}^{2 n} \frac{1}{k!}} \frac{x^{n}}{n}$ $= (e^{- 1} - 1) \sum_{n = 1}^{\infty} \frac{(2 n)!}{n} x^{n} + e^{- 1} \sum_{n = 1}^{\infty} \frac{(2 n)!}{n} (\sum_{k = 1}^{2 n} \frac{1}{k!}) x^{n}$ $. . . . . b e c o n t i n u e d . . . .$
	Answered by mind is power last updated on 11/Nov/19
	$f(x)=[−e^(−t) ln(1−xt^2 )]_0 ^1 +∫_0 ^1 ((e^(−t) .−2xt)/(1−xt^2 ))dt =−e^(−1) ln(1−x)−2x∫_0 ^1 .((te^(−t) dt)/((1−(√x)t)(1+(√x)t))) =−e^(−1) ln(1−x)−(√x)∫_0 ^1 ((e^(−t) .(1+t(√x)−(1−t(√x))))/((1−t(√x))(1+t(√x))))dt =−e^(−1) ln(1−x)−(√x)∫_0 ^1 ((e^(−t) dt)/(1−t(√x)))+(√x)∫_0 ^1 ((e^(−t) dt)/(1+t(√x))) let u=1−t(√x) in first and s=1+t(√x) in 2nd =−e^(−1) ln(1−x)+∫_1 ^(1−(√x)) (e^((u−1)/(√x)) /u)du+∫_1 ^(1+(√x)) (e^((1−s)/(√x)) /s)ds m=(u/(√x)) in first m=(s/(√x)) in]2nd =−e^(−1) ln(1−x)+∫^((1/(√x))−1) _(1/(√x)) ((e^m .e^(−(1/(√x))) )/m).dm+∫_(1/(√x)) ^(1+(1/(√x))) e^(1/(√x)) .e^(−m) .(dm/m)346 We use Ei(w)=∫_(−∞) ^w (e^x /x)dx=∫_∞ ^(−w) (e^(−x) /x)dx Ei is exponential integral function we get −e^(−1) ln(1−x)+{Ei((1/(√x))−1)−Ei((1/(√x)))}e^((−1)/(√x)) +e^(1/(√x)) {Ei(−1−(1/(√x)))−Ei(−(1/(√x)))} ∫_0 ^1 e^(−t) ln(1−(t^2 /2))dt put x=(1/2) =e^(−1) ln(2)+{Ei((1/(√2))−1)−Ei((1/(√2)))}e^(−(1/(√2))) +e^(1/(√2)) {Ei(−1−(1/(√2)))−Ei((1/(√2)))}$
	$f (x) = {[- e^{- t} l n (1 - {x t}^{2})]}_{0}^{1} + \int_{0}^{1} \frac{e^{- t} . - 2 x t}{1 - {x t}^{2}} d t$ $= - e^{- 1} l n (1 - x) - 2 x \int_{0}^{1} . \frac{{t e}^{- t} d t}{(1 - \sqrt{x} t) (1 + \sqrt{x} t)}$ $= - e^{- 1} l n (1 - x) - \sqrt{x} \int_{0}^{1} \frac{e^{- t} . (1 + t \sqrt{x} - (1 - t \sqrt{x}))}{(1 - t \sqrt{x}) (1 + t \sqrt{x})} d t$ $= - e^{- 1} l n (1 - x) - \sqrt{x} \int_{0}^{1} \frac{e^{- t} d t}{1 - t \sqrt{x}} + \sqrt{x} \int_{0}^{1} \frac{e^{- t} d t}{1 + t \sqrt{x}}$ $l e t u = 1 - t \sqrt{x} i n f i r s t a n d s = 1 + t \sqrt{x} i n 2 n d$ $= - e^{- 1} l n (1 - x) + \int_{1}^{1 - \sqrt{x}} \frac{e^{\frac{u - 1}{\sqrt{x}}}}{u} d u + \int_{1}^{1 + \sqrt{x}} \frac{e^{\frac{1 - s}{\sqrt{x}}}}{s} d s$ $m = \frac{u}{\sqrt{x}} i n f i r s t m = \frac{s}{\sqrt{x}} i n] 2 n d$ $= - e^{- 1} l n (1 - x) + {\int_{\frac{1}{\sqrt{x}}}}^{\frac{1}{\sqrt{x}} - 1} \frac{e^{m} . e^{- \frac{1}{\sqrt{x}}}}{m} . d m + \int_{\frac{1}{\sqrt{x}}}^{1 + \frac{1}{\sqrt{x}}} e^{\frac{1}{\sqrt{x}}} . e^{- m} . \frac{d m}{m} 346$ $W e u s e E i (w) = \int_{- \infty}^{w} \frac{e^{x}}{x} d x = \int_{\infty}^{- w} \frac{e^{- x}}{x} d x$ $E i i s e x p o n e n t i a l i n t e g r a l f u n c t i o n$ $w e g e t - e^{- 1} l n (1 - x) + {E i (\frac{1}{\sqrt{x}} - 1) - E i (\frac{1}{\sqrt{x}})} e^{\frac{- 1}{\sqrt{x}}} + e^{\frac{1}{\sqrt{x}}} {E i (- 1 - \frac{1}{\sqrt{x}}) - E i (- \frac{1}{\sqrt{x}})}$ $\int_{0}^{1} e^{- t} l n (1 - \frac{t^{2}}{2}) d t p u t x = \frac{1}{2}$ $= e^{- 1} l n (2) + {E i (\frac{1}{\sqrt{2}} - 1) - E i (\frac{1}{\sqrt{2}})} e^{- \frac{1}{\sqrt{2}}} + e^{\frac{1}{\sqrt{2}}} {E i (- 1 - \frac{1}{\sqrt{2}}) - E i (\frac{1}{\sqrt{2}})}$
	Commented bymind is power last updated on 11/Nov/19

	$y^{'} r e w e l c o m$
	Commented bymathmax by abdo last updated on 11/Nov/19

	$t h a n k y o u s i r .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum