
Question and Answers Forum
Question Number 73429 by Henri Boucatchou last updated on 12/Nov/19
![Solve : ∫(([cos^(−1) x(√(1−x^2 ))]^(−1) )/(log_e [2+((sin(2x(√(1−x^2 ))))/π)]))dx Evaluate ∫_(−π/2) ^( π/2) sin^2 xcos^2 x(cosx+sinx)dx](Q73429.png)
Commented by MJS last updated on 12/Nov/19
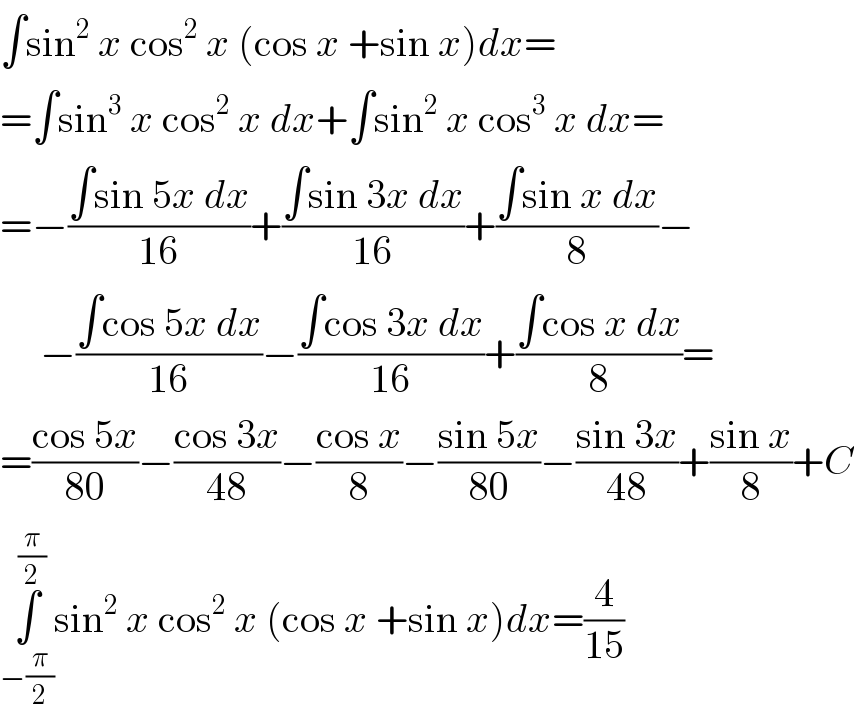
Commented by MJS last updated on 12/Nov/19

Commented by MJS last updated on 12/Nov/19
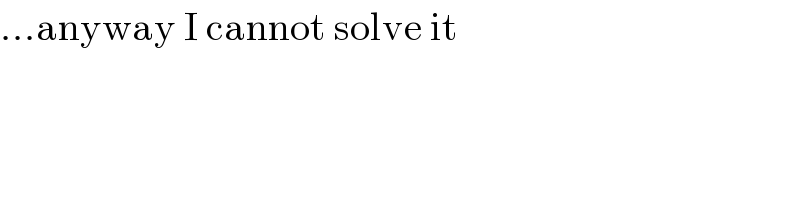
Answered by MJS last updated on 12/Nov/19
![∫sin^2 x cos^2 x (cos x +sin x)dx= =∫sin^3 x cos^2 x dx+∫sin^2 x cos^3 x dx= [u=cos x → dx=−(du/(sin x)); v=sin x → dx=(dv/(cos x))] =∫u^4 −u^2 du+∫v^2 −v^4 dv= =(u^5 /5)−(u^3 /3)+(v^3 /3)−(v^5 /5)= =((cos^5 x)/5)−((cos^3 x)/3)+((sin^3 x)/3)−((sin^5 x)/5)+C ∫_(−(π/2)) ^(π/2) sin^2 x cos^2 x (cos x +sin x)dx=(4/(15))](Q73432.png)
