Question Number 73466 by Rio Michael last updated on 12/Nov/19
$${please}\:{explain}\:{this}\: \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {{Lim}}\frac{{sinx}}{{x}}\:=\:\mathrm{1}\:\:{by}\:{l}'{hopitals}\:{theorem} \\ $$$$ \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {{Lim}}\:\frac{{sinx}}{{x}}\:=\:\mathrm{0}\:{by}\:{Squeez}\:{theorem} \\ $$$${is}\:{there}\:{something}\:{wrong}? \\ $$
Answered by MJS last updated on 12/Nov/19
![lim_(x→0) ((sin x)/x) =1 by Squeeze theorem: draw a quarter circle within x^+ , y^+ [or for 0≤α≤(π/2)] you can see that tan α ≥arc≥sin α arc=α tan α ≥α≥sin α ((sin α)/(cos α))≥α≥sin α ((cos α)/(sin α))≤(1/α)≤(1/(sin α)) cos α ≤ ((sin α)/α)≤1 lim_(α→0) cos α =1 ⇒ lim_(x→0) ((sin x)/x) =1](Q73471.png)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}}{{x}}\:=\mathrm{1}\:\mathrm{by}\:\mathrm{Squeeze}\:\mathrm{theorem}: \\ $$$$\mathrm{draw}\:\mathrm{a}\:\mathrm{quarter}\:\mathrm{circle}\:\mathrm{within}\:{x}^{+} ,\:{y}^{+} \:\left[\mathrm{or}\:\mathrm{for}\right. \\ $$$$\left.\mathrm{0}\leqslant\alpha\leqslant\frac{\pi}{\mathrm{2}}\right] \\ $$$$\mathrm{you}\:\mathrm{can}\:\mathrm{see}\:\mathrm{that} \\ $$$$\mathrm{tan}\:\alpha\:\geqslant{arc}\geqslant\mathrm{sin}\:\alpha \\ $$$${arc}=\alpha \\ $$$$\mathrm{tan}\:\alpha\:\geqslant\alpha\geqslant\mathrm{sin}\:\alpha \\ $$$$\frac{\mathrm{sin}\:\alpha}{\mathrm{cos}\:\alpha}\geqslant\alpha\geqslant\mathrm{sin}\:\alpha \\ $$$$\frac{\mathrm{cos}\:\alpha}{\mathrm{sin}\:\alpha}\leqslant\frac{\mathrm{1}}{\alpha}\leqslant\frac{\mathrm{1}}{\mathrm{sin}\:\alpha} \\ $$$$\mathrm{cos}\:\alpha\:\leqslant\:\frac{\mathrm{sin}\:\alpha}{\alpha}\leqslant\mathrm{1} \\ $$$$\underset{\alpha\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{cos}\:\alpha\:=\mathrm{1} \\ $$$$\Rightarrow\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}}{{x}}\:=\mathrm{1} \\ $$
Commented by Rio Michael last updated on 13/Nov/19
$${thanks}\:{sir},\:{i}\:{was}\:{thinking} \\ $$$${i}\:{will}\:{use}\: \\ $$$$\:\:\:\:\:−\mathrm{1}\leqslant\:{sinx}\:\leqslant\:\mathrm{1} \\ $$$$\:\:\Rightarrow\:\:−\frac{\mathrm{1}}{{x}}\:\leqslant\:\frac{{sinx}}{{x}}\:\leqslant\:\frac{\mathrm{1}}{{x}} \\ $$$$\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:−\frac{\mathrm{1}}{{x}}\:\leqslant\:\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{sinx}}{{x}}\:\leqslant\underset{{x}\rightarrow\mathrm{0}} {\:{lim}}\:\frac{\mathrm{1}}{{x}} \\ $$$$\:\:\:\:\mathrm{0}\:\leqslant\:\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{sinx}}{{x}}\:\leqslant\:\mathrm{0} \\ $$$$\therefore\:\:\underset{{x}\rightarrow\mathrm{0}} {{lim}}\frac{{sinx}}{{x}}\:=\:\mathrm{0} \\ $$
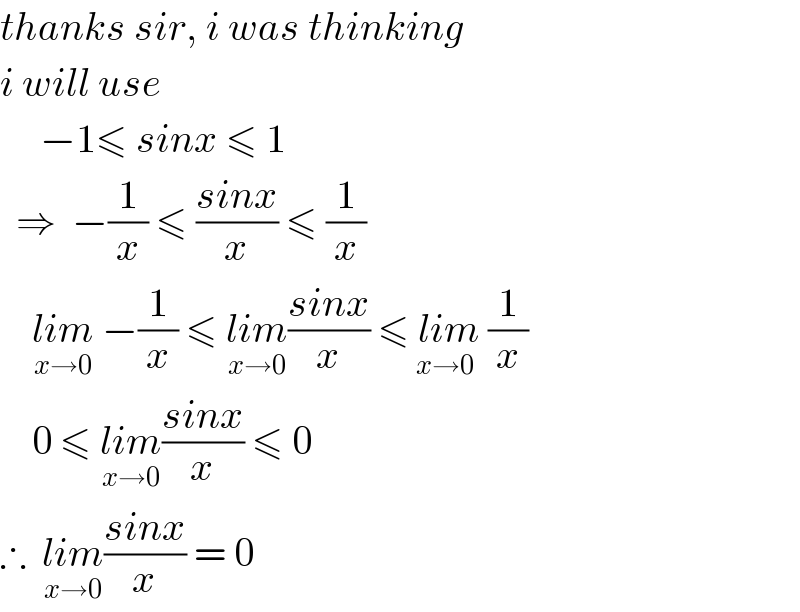
Commented by MJS last updated on 13/Nov/19
$$\mathrm{this}\:\mathrm{is}\:\mathrm{not}\:\mathrm{possible}\:\mathrm{because} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\pm\frac{\mathrm{1}}{{x}}=\pm\infty \\ $$
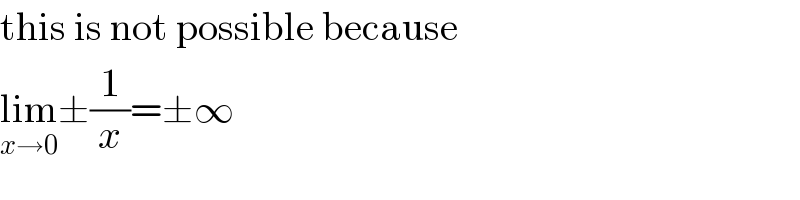
Commented by Rio Michael last updated on 13/Nov/19
$${thanks}\:{sir}\: \\ $$