Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 73488 by abdomathmax last updated on 13/Nov/19

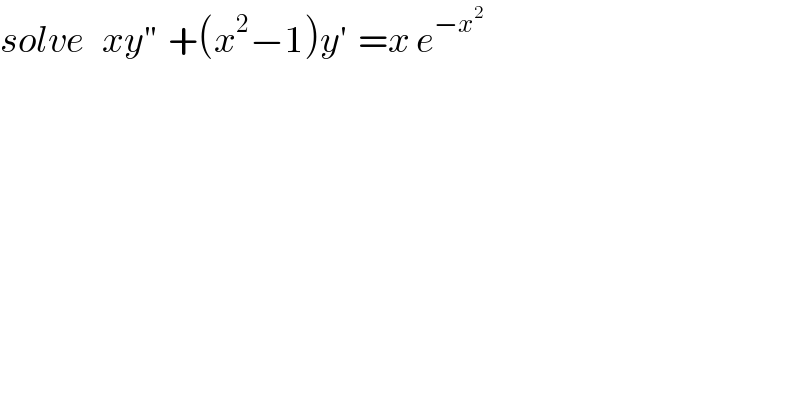
solve xy^(′′) +(x^2 −1)y^′ =x e^(−x^2 )

$${solve}\:\:\:{xy}^{''} \:\:+\left({x}^{\mathrm{2}} −\mathrm{1}\right){y}^{'} \:\:={x}\:{e}^{−{x}^{\mathrm{2}} } \\ $$

Commented by mathmax by abdo last updated on 14/Nov/19

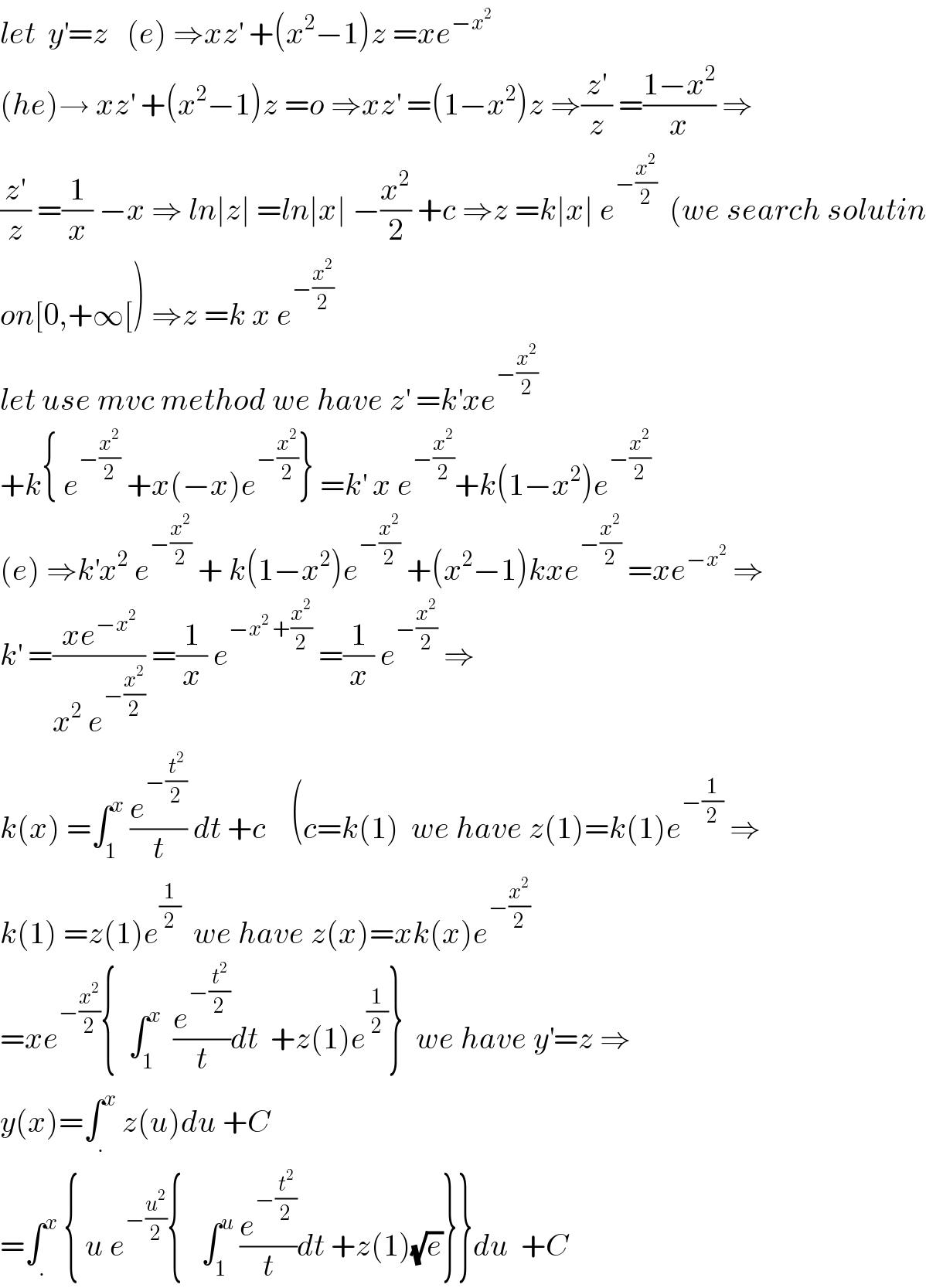
let y^′ =z (e) ⇒xz^′ +(x^2 −1)z =xe^(−x^2 ) (he)→ xz^′ +(x^2 −1)z =o ⇒xz^′ =(1−x^2 )z ⇒(z^′ /z) =((1−x^2 )/x) ⇒ (z^′ /z) =(1/x) −x ⇒ ln∣z∣ =ln∣x∣ −(x^2 /2) +c ⇒z =k∣x∣ e^(−(x^2 /2)) (we search solutin on[0,+∞[) ⇒z =k x e^(−(x^2 /2)) let use mvc method we have z^′ =k^′ xe^(−(x^2 /2)) +k{ e^(−(x^2 /2)) +x(−x)e^(−(x^2 /2)) } =k^′ x e^(−(x^2 /2)) +k(1−x^2 )e^(−(x^2 /2)) (e) ⇒k^′ x^2 e^(−(x^2 /2)) + k(1−x^2 )e^(−(x^2 /2)) +(x^2 −1)kxe^(−(x^2 /2)) =xe^(−x^2 ) ⇒ k^′ =((xe^(−x^2 ) )/(x^2 e^(−(x^2 /2)) )) =(1/x) e^(−x^2 +(x^2 /2)) =(1/x) e^(−(x^2 /2)) ⇒ k(x) =∫_1 ^x (e^(−(t^2 /2)) /t) dt +c (c=k(1) we have z(1)=k(1)e^(−(1/2)) ⇒ k(1) =z(1)e^(1/2) we have z(x)=xk(x)e^(−(x^2 /2)) =xe^(−(x^2 /2)) { ∫_1 ^x (e^(−(t^2 /2)) /t)dt +z(1)e^(1/2) } we have y^′ =z ⇒ y(x)=∫_. ^x z(u)du +C =∫_. ^x { u e^(−(u^2 /2)) { ∫_1 ^u (e^(−(t^2 /2)) /t)dt +z(1)(√e)}}du +C

$${let}\:\:{y}^{'} ={z}\:\:\:\left({e}\right)\:\Rightarrow{xz}^{'} \:+\left({x}^{\mathrm{2}} −\mathrm{1}\right){z}\:={xe}^{−{x}^{\mathrm{2}} } \\ $$$$\left({he}\right)\rightarrow\:{xz}^{'} \:+\left({x}^{\mathrm{2}} −\mathrm{1}\right){z}\:={o}\:\Rightarrow{xz}^{'} \:=\left(\mathrm{1}−{x}^{\mathrm{2}} \right){z}\:\Rightarrow\frac{{z}^{'} }{{z}}\:=\frac{\mathrm{1}−{x}^{\mathrm{2}} }{{x}}\:\Rightarrow \\ $$$$\frac{{z}^{'} }{{z}}\:=\frac{\mathrm{1}}{{x}}\:−{x}\:\Rightarrow\:{ln}\mid{z}\mid\:={ln}\mid{x}\mid\:−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+{c}\:\Rightarrow{z}\:={k}\mid{x}\mid\:{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:\:\left({we}\:{search}\:{solutin}\right. \\ $$$${on}\left[\mathrm{0},+\infty\left[\right)\:\Rightarrow{z}\:={k}\:{x}\:{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \right. \\ $$$${let}\:{use}\:{mvc}\:{method}\:{we}\:{have}\:{z}^{'} \:={k}^{'} {xe}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$+{k}\left\{\:{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:+{x}\left(−{x}\right){e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \right\}\:={k}^{'} \:{x}\:{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} +{k}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$\left({e}\right)\:\Rightarrow{k}^{'} {x}^{\mathrm{2}} \:{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:+\:{k}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:+\left({x}^{\mathrm{2}} −\mathrm{1}\right){kxe}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:={xe}^{−{x}^{\mathrm{2}} } \:\Rightarrow \\ $$$${k}^{'} \:=\frac{{xe}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} \:{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} }\:=\frac{\mathrm{1}}{{x}}\:{e}^{−{x}^{\mathrm{2}} \:+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:=\frac{\mathrm{1}}{{x}}\:{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:\Rightarrow \\ $$$${k}\left({x}\right)\:=\int_{\mathrm{1}} ^{{x}} \:\frac{{e}^{−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} }{{t}}\:{dt}\:+{c}\:\:\:\:\left({c}={k}\left(\mathrm{1}\right)\:\:{we}\:{have}\:{z}\left(\mathrm{1}\right)={k}\left(\mathrm{1}\right){e}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\Rightarrow\right. \\ $$$${k}\left(\mathrm{1}\right)\:={z}\left(\mathrm{1}\right){e}^{\frac{\mathrm{1}}{\mathrm{2}}} \:\:{we}\:{have}\:{z}\left({x}\right)={xk}\left({x}\right){e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$={xe}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \left\{\:\:\int_{\mathrm{1}} ^{{x}} \:\:\frac{{e}^{−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} }{{t}}{dt}\:\:+{z}\left(\mathrm{1}\right){e}^{\frac{\mathrm{1}}{\mathrm{2}}} \right\}\:\:{we}\:{have}\:{y}^{'} ={z}\:\Rightarrow \\ $$$${y}\left({x}\right)=\int_{.} ^{{x}} \:{z}\left({u}\right){du}\:+{C}\: \\ $$$$=\int_{.} ^{{x}} \:\left\{\:{u}\:{e}^{−\frac{{u}^{\mathrm{2}} }{\mathrm{2}}} \left\{\:\:\:\int_{\mathrm{1}} ^{{u}} \:\frac{{e}^{−\frac{{t}^{\mathrm{2}} }{\mathrm{2}}} }{{t}}{dt}\:+{z}\left(\mathrm{1}\right)\sqrt{{e}}\right\}\right\}{du}\:\:+{C} \\ $$

Answered by mind is power last updated on 13/Nov/19

y′=z homgen xz′+(x^2 −1)z=0 ⇒((z′)/z)=(1/x)−x⇒ln∣z∣=−(x^2 /2)+ln(x)⇒z=kxe^(−(x^2 /2)) xz′+(x^2 −1)z=xe^(−x^2 ) x(k′xe^(−(x^2 /2)) +(e^(−(x^2 /2)) −x^2 e^((−x^2 )/2) )k)+(x^2 −1)kxe^(−(x^2 /2)) =xe^(−x^2 ) ⇒k′x^2 e^(−(x^2 /2)) =xe^(−x^2 ) k′=(e^(−(x^2 /2)) /x) k=∫(e^(−x^2 ) /x)dx x=(√t)⇒dx=(dt/(2(√t))) ∫(e^(−t) /(2t))dt=∫(e^t /(2t))dt=(1/2)E_i (−t) E_i =exponential integral function ⇒k=((Ei(−x^2 ))/2)+c ⇒z(x)=xe^(−(x^2 /2)) {∫(e^(−x^2 ) /x)dx+c}=(1/2)xe^(−(x^2 /2)) Ei(−x^2 )+c((xe^(−(x^2 /2)) )/2) y=∫z(x)dx by part =−(e^(−(x^2 /2)) /2)Ei(−x^2 )+(1/2)∫e^(−(x^2 /2)) .(e^(−x^2 ) /x)dx−(c/4)xe^(−(x^2 /2)) =−(e^(−(x^2 /2)) /2)E_i (−x^2 )+(1/2)∫(e^(−((3/2))x^2 ) /x)dx (3/2)x^2 =t⇒(1/2)∫ ((e^(−t) )/t).dt=(1/2)E_i (−t)=(1/2)E_i (−(3/2)x^2 )+d y(x)=−(e^(−(x^2 /2)) /2)E_i (−x^2 )+(1/4)E_i (−((3x^2 )/2))−((cxe^(−(x^2 /2)) )/4)+d c,d constante

$${y}'={z} \\ $$$${homgen} \\ $$$${xz}'+\left({x}^{\mathrm{2}} −\mathrm{1}\right){z}=\mathrm{0} \\ $$$$\Rightarrow\frac{{z}'}{{z}}=\frac{\mathrm{1}}{{x}}−{x}\Rightarrow{ln}\mid{z}\mid=−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{ln}\left({x}\right)\Rightarrow{z}={kxe}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$${xz}'+\left({x}^{\mathrm{2}} −\mathrm{1}\right){z}={xe}^{−{x}^{\mathrm{2}} } \\ $$$${x}\left({k}'{xe}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} +\left({e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} −{x}^{\mathrm{2}} {e}^{\frac{−{x}^{\mathrm{2}} }{\mathrm{2}}} \right){k}\right)+\left({x}^{\mathrm{2}} −\mathrm{1}\right){kxe}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} ={xe}^{−{x}^{\mathrm{2}} } \\ $$$$\Rightarrow{k}'{x}^{\mathrm{2}} {e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} ={xe}^{−{x}^{\mathrm{2}} } \\ $$$${k}'=\frac{{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} }{{x}} \\ $$$${k}=\int\frac{{e}^{−{x}^{\mathrm{2}} } }{{x}}{dx} \\ $$$${x}=\sqrt{{t}}\Rightarrow{dx}=\frac{{dt}}{\mathrm{2}\sqrt{{t}}} \\ $$$$\int\frac{{e}^{−{t}} }{\mathrm{2}{t}}{dt}=\int\frac{{e}^{{t}} }{\mathrm{2}{t}}{dt}=\frac{\mathrm{1}}{\mathrm{2}}{E}_{{i}} \left(−{t}\right) \\ $$$${E}_{{i}} ={exponential}\:{integral}\:{function} \\ $$$$\Rightarrow{k}=\frac{{Ei}\left(−{x}^{\mathrm{2}} \right)}{\mathrm{2}}+{c} \\ $$$$\Rightarrow{z}\left({x}\right)={xe}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \left\{\int\frac{{e}^{−{x}^{\mathrm{2}} } }{{x}}{dx}+{c}\right\}=\frac{\mathrm{1}}{\mathrm{2}}{xe}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} {Ei}\left(−{x}^{\mathrm{2}} \right)+{c}\frac{{xe}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} }{\mathrm{2}} \\ $$$${y}=\int{z}\left({x}\right){dx} \\ $$$${by}\:{part}\:\:=−\frac{{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} }{\mathrm{2}}{Ei}\left(−{x}^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{2}}\int{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} .\frac{{e}^{−{x}^{\mathrm{2}} } }{{x}}{dx}−\frac{{c}}{\mathrm{4}}{xe}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$=−\frac{{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} }{\mathrm{2}}{E}_{{i}} \left(−{x}^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{e}^{−\left(\frac{\mathrm{3}}{\mathrm{2}}\right){x}^{\mathrm{2}} } }{{x}}{dx} \\ $$$$\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} ={t}\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{e}^{−{t}} \:}{{t}}.{dt}=\frac{\mathrm{1}}{\mathrm{2}}{E}_{{i}} \left(−{t}\right)=\frac{\mathrm{1}}{\mathrm{2}}{E}_{{i}} \left(−\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} \right)+{d} \\ $$$${y}\left({x}\right)=−\frac{{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} }{\mathrm{2}}{E}_{{i}} \left(−{x}^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{4}}{E}_{{i}} \left(−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}\right)−\frac{{cxe}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} }{\mathrm{4}}+{d} \\ $$$${c},{d}\:{constante} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Answered by arkanmath7@gmail.com last updated on 13/Nov/19

let y^′ = p , y′′ = p^′ xp^′ + (x^2 − 1)p = xe^(−x^2 ) /x p^′ + (x − (1/x))p = e^(−x^2 ) P (x) = x − (1/x) , Q (x) = e^(−x^2 ) p = e^(−∫P (x)dx) [∫Q (x) e^(∫P (x)dx) dx] p = e^(−∫(x−(1/x))dx) [∫e^(−x^2 ) e^(∫(x − (1/x))dx) dx] p = e^(−(x^2 /2) + lnx) [∫e^(−x^2 ) e^((x^2 /2) − lnx) dx] p = e^(−(x^2 /2)) e^( lnx) [∫e^(−x^2 ) e^((x^2 /2) ) e^(lnx ) dx] p = xe^(−(x^2 /2)) [∫−x e^(−(1/2)x^2 ) dx] p = xe^(−(x^2 /2)) [(1/2) e^(−(1/2)x^2 ) + c] p = (1/2)xe^(−x^2 ) + cxe^(−(x^2 /2)) (dy/dx) = (1/2)xe^(−x^2 ) + cxe^(−(x^2 /2)) dy = ((1/2)xe^(−x^2 ) + cxe^(−(x^2 /2)) )dx ∫dy = ∫((1/2)xe^(−x^2 ) + cxe^(−(x^2 /2)) )dx y = − (1/4) e^(−x^2 ) −ce^(−(x^2 /2)) + c_1

$${let}\:\:{y}^{'} \:=\:{p}\:\:\:,\:\:\:{y}''\:=\:{p}^{'} \\ $$$${xp}\:^{'} \:+\:\left({x}^{\mathrm{2}} \:−\:\mathrm{1}\right){p}\:=\:{xe}^{−{x}^{\mathrm{2}} } \:\:\:\:\:\:\:/{x} \\ $$$${p}^{'} \:\:+\:\left({x}\:−\:\frac{\mathrm{1}}{{x}}\right){p}\:=\:{e}^{−{x}^{\mathrm{2}} } \\ $$$${P}\:\left({x}\right)\:=\:{x}\:−\:\frac{\mathrm{1}}{{x}}\:\:\:,\:\:\:{Q}\:\left({x}\right)\:=\:{e}^{−{x}^{\mathrm{2}} } \\ $$$${p}\:=\:{e}^{−\int{P}\:\left({x}\right){dx}} \:\left[\int{Q}\:\left({x}\right)\:{e}^{\int{P}\:\left({x}\right){dx}} \:\:{dx}\right] \\ $$$${p}\:=\:{e}^{−\int\left({x}−\frac{\mathrm{1}}{{x}}\right){dx}} \:\left[\int{e}^{−{x}^{\mathrm{2}} } {e}^{\int\left({x}\:−\:\frac{\mathrm{1}}{{x}}\right){dx}} \:\:{dx}\right] \\ $$$${p}\:=\:{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+\:{lnx}} \:\left[\int{e}^{−{x}^{\mathrm{2}} } {e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:−\:{lnx}} \:\:{dx}\right] \\ $$$${p}\:=\:{e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:{e}^{\:{lnx}} \:\left[\int{e}^{−{x}^{\mathrm{2}} } {e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:} \:{e}^{{lnx}\:} {dx}\right] \\ $$$$ \\ $$$${p}\:=\:{xe}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:\left[\int−{x}\:{e}^{−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} } {dx}\right] \\ $$$${p}\:=\:{xe}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:\left[\frac{\mathrm{1}}{\mathrm{2}}\:{e}^{−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} } \:+\:{c}\right] \\ $$$${p}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{xe}^{−{x}^{\mathrm{2}} } \:\:+\:{cxe}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{xe}^{−{x}^{\mathrm{2}} } \:\:+\:{cxe}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$$ \\ $$$${dy}\:=\:\left(\frac{\mathrm{1}}{\mathrm{2}}{xe}^{−{x}^{\mathrm{2}} } \:\:+\:{cxe}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \right){dx} \\ $$$$ \\ $$$$\int{dy}\:=\:\int\left(\frac{\mathrm{1}}{\mathrm{2}}{xe}^{−{x}^{\mathrm{2}} } \:\:+\:{cxe}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \right){dx} \\ $$$$ \\ $$$${y}\:=\:−\:\frac{\mathrm{1}}{\mathrm{4}}\:{e}^{−{x}^{\mathrm{2}} \:} −{ce}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:+\:{c}_{\mathrm{1}} \\ $$

Commented by mind is power last updated on 13/Nov/19

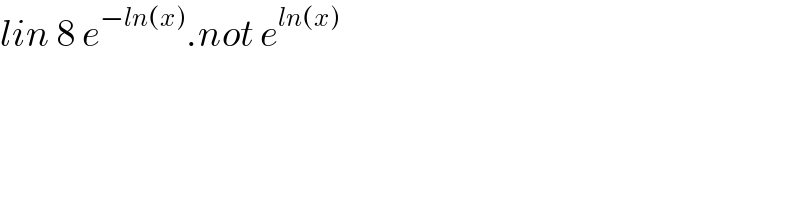
lin 8 e^(−ln(x)) .not e^(ln(x))

$${lin}\:\mathrm{8}\:{e}^{−{ln}\left({x}\right)} .{not}\:{e}^{{ln}\left({x}\right)} \\ $$

Commented by arkanmath7@gmail.com last updated on 13/Nov/19

yes true

$${yes}\:{true} \\ $$

Commented by arkanmath7@gmail.com last updated on 13/Nov/19

mistake!

$${mistake}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com